11. Similar Shapes (level 3-5) - Cardiff Tutor Company

Question 1

LEVEL 4

Given that shapes A and B are similar, and that shape B is a scale factor of 2.5 times bigger than A, work out the perimeter of B.

Select the correct answer from the list below:

A: $160$ cm

B: $16$ cm

C: $40$ cm

D: $100$ cm

CORRECT ANSWER: D: $100$ cm

WORKED SOLUTION:

We can do this in two ways.

Method 1

We know that B is $2.5$ times bigger than A, so each side must be $2.5$ times longer.

$10\times2.5=25$
$5\times2.5=12.5$

And now we just need to add them all together

$25+25+12.5+12.5+12.5+12.5=100$ cm

Method 2

The perimeter of shape A is:

$10+10+5+5+5+5=40$ cm

And now, to find the perimeter of shape B, we just need to multiply by $2.5$

$40\times2.5=100$ cm

Question 2

LEVEL 4

Below are two similar triangles.

Find the value of $x$

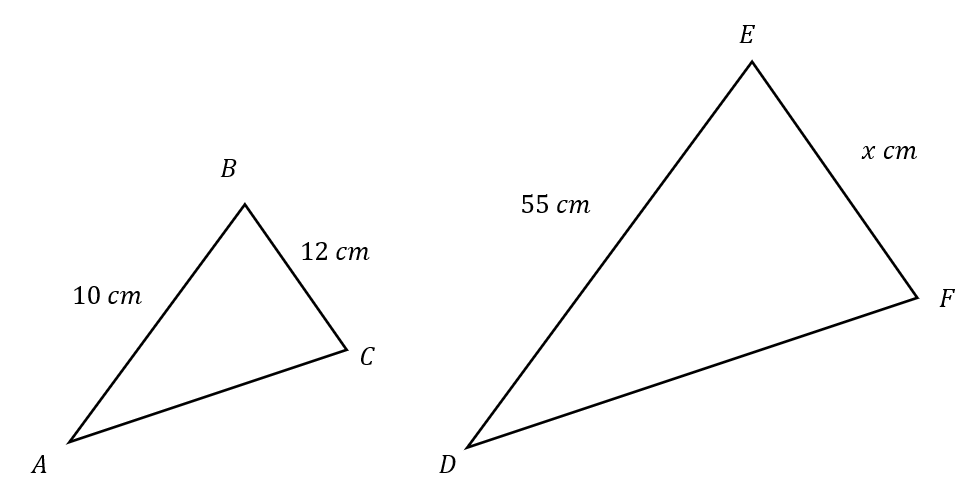
Select the correct answer from the list below:

A: $66$ cm

B: $70$ cm

C: $62$ cm

D: $58$ cm

CORRECT ANSWER: A: $66$ cm

WORKED SOLUTION:

As the lengths $AB$ and $DE$ are similar, we can determine the scale factor as $5.5$

Hence $EF$ will also be $5.5$ times larger than $BC$ so,

$x=5.5\times12=66$ cm

Question 3

LEVEL 4

Below are two similar triangles.

$AB = 55$ cm

Find the value of $AD$

Select the correct answer from the list below:

A: $18$ cm

B: $22$ cm

C: $26$ cm

D: $16$ cm

CORRECT ANSWER: B: $22$ cm

WORKED SOLUTION:

First we have to find the scale factor between the two triangles,

Scale factor = $25\div 10 = 2.5$

Hence if we divide the length $AD$ by this scale factor we will get the length $AB$ ,

$AB = 55\div2.5 = 22$ cm

Question 4

LEVEL 4

Below are two similar triangles.

$AD= 3.5$ cm

Find the value of $AB$

Select the correct answer from the list below:

A: $28$ cm

B: $20$ cm

C: $25$ cm

D: $35$ cm

CORRECT ANSWER: A: $28$ cm

WORKED SOLUTION:

First we have to find the scale factor between the two triangles,

Scale factor = $20\div2.5 = 8$

Hence if we multiply the length $AD$ by this scale factor we will get the length $AB$ ,

$AB = 3.5 \times 8 = 28$ cm

Question 5

LEVEL 4

Below are two similar regular pentagons, shape $A$ with side length $4$ cm and shape $B$ with side length $6$ cm.

Determine the scale factor between the shapes.

A: $1.5$

B: $1.25$

C: $2$

D: $24$

CORRECT ANSWER: A: $1.5$

WORKED SOLUTION:

To find the scale factor between the shapes, we do

Scale factor = $6\div 4 = 1.5$