1. Pythagoras - Cardiff Tutor Company

Question 1

LEVEL 4

Calculate the length of side $c$ .

Select the correct answer from the list below:

A: $6.9$ cm

B: $8.2$ cm

C: $9.1$ cm

D: $7.4$ cm

CORRECT ANSWER: D: $7.4$ cm

WORKED SOLUTION:

In order to calculate the length of $c$ we can use Pythagoras theorem that states,

$c^2=a^2+b^2$

Here we are given the values of $a$ and $b$ so can substitute them into this equation

$c^2=3.3^2+6.6^2=54.45$

To find the length $c$ we have to square root both sides of the equation and only consider the positive solution as $c$ represents a physical length which means that negative solution can be ignored.

$c=\sqrt {54.45}=7.4$ cm

Question 2

LEVEL 4

Calculate the length of side $b$ .

Select the correct answer from the list below:

A: $4.9$ cm

B: $5.7$ cm

C: $5.3$ cm

D: $4.7$ cm

CORRECT ANSWER: B: $5.7$ cm

WORKED SOLUTION:

In order to calculate the length of $b$ , we can use Pythagoras theorem that states,

$c^2=a^2+b^2$

Here we are given the values of $a$ and $c$ so can substitute them into a rearranged version of this equation

$6.6^2-3.3^2=b^2=32.67$

To find the length $b$ we have to square root both sides of the equation and only consider the positive solution as $b$ represents a physical length which means that negative solution can be ignored.

$b=\sqrt {32.67}=5.7$ cm

Question 3

LEVEL 4

Calculate the length of the book, if its width is $3.7$ cm and diagonally it is $9.5$ cm.

Select the correct answer from the list below:

A: $6.85$ cm

B: $7.38$ cm

C: $8.22$ cm

D: $8.75$ cm

CORRECT ANSWER: D: $8.75$ cm

WORKED SOLUTION:

In order to calculate the length of $b$ , we can use Pythagoras theorem that states,

$c^2=a^2+b^2$

Here we are given the values of $a$ and $c$ so can substitute them into a rearranged version of this equation

$9.5^2-3.7^2=b^2=76.56$

To find the length $b$ we have to square root both sides of the equation and only consider the positive solution as $b$ represents a physical length which means that negative solution can be ignored.

$b=\sqrt {76.56}=8.75$ cm

Question 4

LEVEL 4

Calculate the diagonal length of the laptop if its width is $4.8$ cm and its length is $9.8$ cm.

Select the correct answer from the list below:

A: $11.1$ cm

B: $11.7$ cm

C: $10.9$ cm

D: $10.7$ cm

CORRECT ANSWER: C: $10.9$ cm

WORKED SOLUTION:

In order to calculate the length of $c$ we can use Pythagoras theorem that states,

$c^2=a^2+b^2$

Here we are given the values of $a$ and $b$ so can substitute them into this equation

$c^2=9.8^2+4.8^2=119.08$

To find the length $c$ we have to square root both sides of the equation and only consider the positive solution as $c$ represents a physical length which means that negative solution can be ignored.

$c=\sqrt {119.08}=10.9$ cm

Question 5

LEVEL 4

British Airways flight $747$ is soon to arrive at Gatwick airport.

The normal runway is $2$ km and the pilot has $7.7$ km of diagonal steering until the plane lands safely at the end of the runway.

Currently, at what height in the air is the plane?

Select the correct answer from the list below:

A: $6.77$ km

B: $7.44$ km

C: $5.35$ km

D: $5.85$ km

CORRECT ANSWER: B: $7.44$ km

WORKED SOLUTION:

In order to calculate the length of $b$ , we can use Pythagoras theorem that states,

$c^2=a^2+b^2$

Here we are given the values of $a$ and $c$ so can substitute them into a rearranged version of this equation

$7.7^2-2^2=b^2=55.29$

To find the length $b$ we have to square root both sides of the equation and only consider the positive solution as $b$ represents a physical length which means that negative solution can be ignored.

$b=\sqrt {55.29}=7.44$ km

Question 6

LEVEL 4

Calculate the width of the door if its height is $1.8$ m and diagonally it is $3.2$ m.

Select the correct answer from the list below:

A: $2.65$ m

B: $2.78$ m

C: $2.56$ m

D: $2.94$ m

CORRECT ANSWER: A: $2.65$ m

WORKED SOLUTION:

In order to calculate the length of $b$ , we can use Pythagoras theorem that states,

$c^2=a^2+b^2$

Here we are given the values of $a$ and $c$ so can substitute them into a rearranged version of this equation

$3.2^2-1.8^2=b^2=7$

To find the length $b$ we have to square root both sides of the equation and only consider the positive solution as $b$ represents a physical length which means that negative solution can be ignored.

$b=\sqrt {7}=2.65$ m

Question 7

LEVEL 4

Calculate the distance between the two points $(-4,1)$ and $(4,5)$ .

Select the correct answer from the list below:

A: $8.94$ m

B: $12$ m

C: $0.5$ m

D: $80$ m

CORRECT ANSWER: A: $8.94$ m

WORKED SOLUTION:

To calculate the distance, we first plot the points on a graph, and draw a line connecting them. We then construct a right-angled triangle:

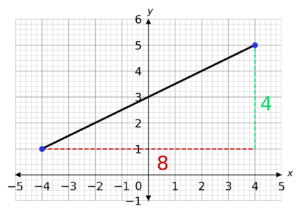
We can see that the distance between the two point is the longest side of the right-angled triangle – the hypotenuse. So we substitute the known values of $a$ and $b$ , into

$a^2 + b^2 = c^2$

$8^2 + 4^2 = c^2 = 80$

To find the length $c$ we have to square root both sides of the equation and only consider the positive solution as $c$ represents a physical length which means that negative solution can be ignored.

$c = \sqrt{80} = 8.94$ cm