Question 1
A triangle ABC is shown below:
Find the value of x
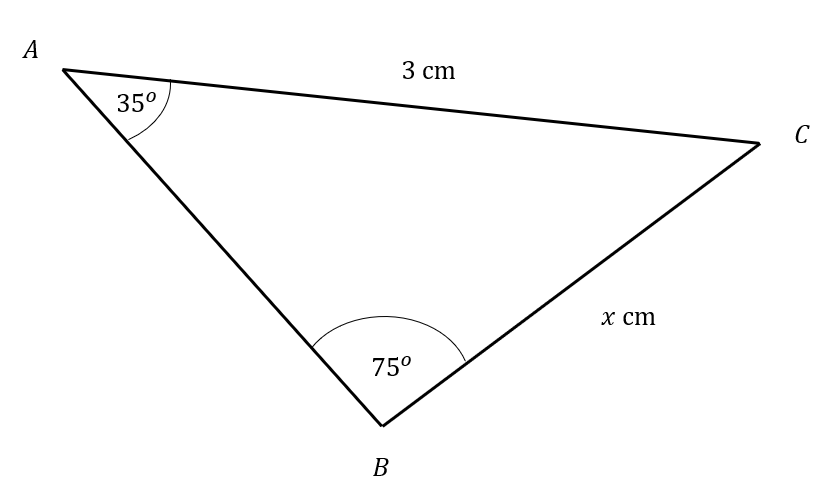
Select the correct answer from the list below:
A: 2.04 cm
B: 1.95 cm
C: 1.84 cm
D: 1.78 cm
CORRECT ANSWER:
WORKED SOLUTION:
To find x we can use the sine rule,
\dfrac{a}{sin(A)}=\dfrac{b}{sin(B)}
Where is this instance we have,
\dfrac{3}{sin(75)}=\dfrac{x}{sin(35)}
Hence by reargning to make x the subject,
x=\dfrac{3sin(35)}{sin(75)}=1.78cm
Question 2
A triangle ABC is shown below:
Find the value of x

Select the correct answer from the list below:
A: 11.67 cm
B: 12.73 cm
C: 10.88 cm
D: 13.10 cm
CORRECT ANSWER:
WORKED SOLUTION:
To find x we can use the sine rule,
\dfrac{a}{sin(A)}=\dfrac{b}{sin(B)}
Where is this instance we have,
\dfrac{15}{sin(40)}=\dfrac{x}{sin(30)}
Hence by reargning to make x the subject,
x=\dfrac{15sin(30)}{sin(40)}=11.67cm
Question 3
A triangle ABC is shown below:
Find the value of x

Select the correct answer from the list below:
A: 92.02 \degree
B: 87.48 \degree
C: 104.33 \degree
D: 96.09 \degree
CORRECT ANSWER:
WORKED SOLUTION:
To find x we can use the sine rule,
\dfrac{sin(A)}{a}=\dfrac{sin(B)}{b}
Where is this instance we have,
\dfrac{sin(x)}{20}=\dfrac{sin(60)}{12}
Hence by rearranging to make x the subject,
x = 92.02 \degree
Question 4
A triangle ABC is shown below:
Find the value of x
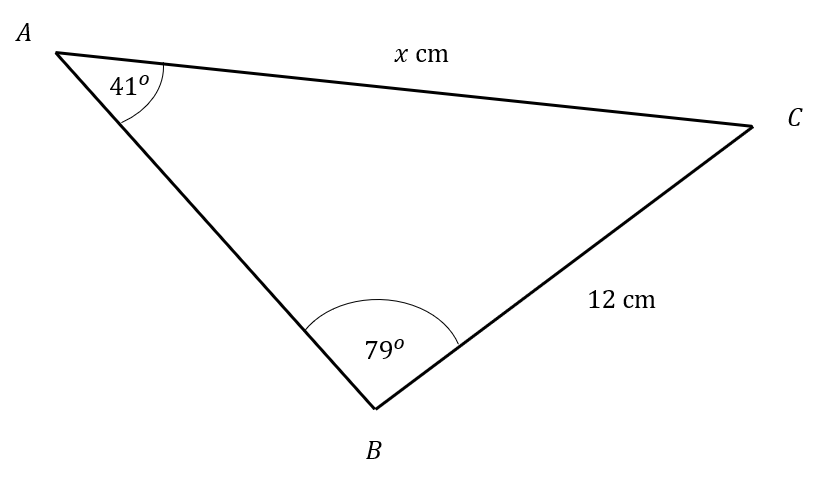
Select the correct answer from the list below:
A: 16.71cm
B: 15.38cm
C: 17.95cm
D: 18.47cm
CORRECT ANSWER: C: 17.95cm
WORKED SOLUTION:
To find x we can use the sine rule,
\dfrac{a}{sin(A)}=\dfrac{b}{sin(B)}
Where is this instance we have,
\dfrac{x}{sin(79)}=\dfrac{12}{sin(41)}
Hence by reargning to make x the subject,
x=\dfrac{12sin(79)}{sin(41)}=17.95cm
Question 5
A triangle ABC is shown below:
Find the value of x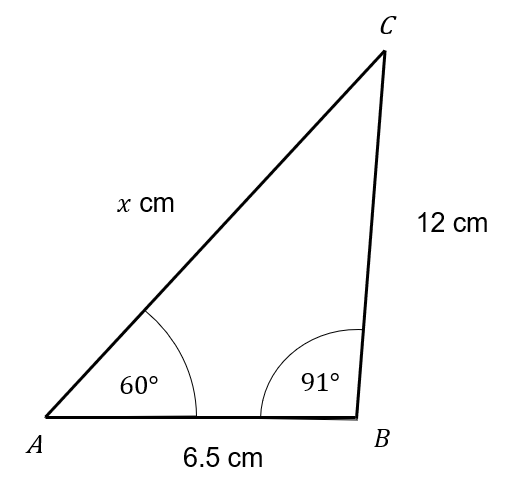
Select the correct answer from the list below:
A: x=15.45
B: x=13.85
C: x=14.25
D: x=13.15
CORRECT ANSWER: B: x=13.85
WORKED SOLUTION:
To find x we can use the sine rule,
\dfrac{a}{sin(A)}=\dfrac{b}{sin(B)}
Where is this instance we have,
\dfrac{x}{sin(91)}=\dfrac{12}{sin(60)}
Hence by rearranging to make x the subject,
x=13.85
