Question 1
LEVEL 6
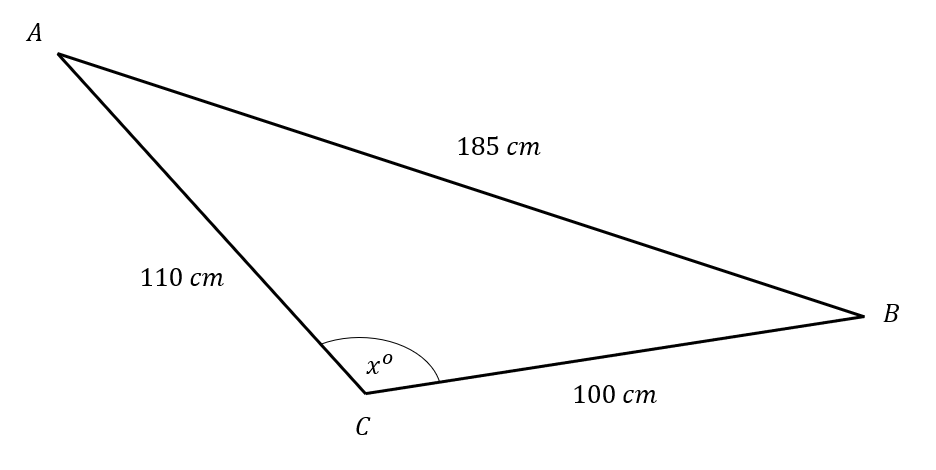
A triangle ABC is shown below:
Angle x is an obtuse angle.
Find the value of x.
Select the correct answer from the list below:
A: 123.4\degree
B: 108.5\degree
C: 115.8\degree
D: 125.9\degree
CORRECT ANSWER: A: 123.4\degree
WORKED SOLUTION:
To calculate x we can use the cosine rule,
\text{cos}(A)=\dfrac{b^2+c^2-a^2}{2bc}
Hence substituting the values in,
\text{cos}(x)=\dfrac{110^2+100^2-185^2}{2(110)(100)}
Taking the inverse cosine of both sides,
x= \text{cos}^{-1} \bigg( \dfrac{-12125}{22000} \bigg) =123.4\degree
Question 2
LEVEL 6
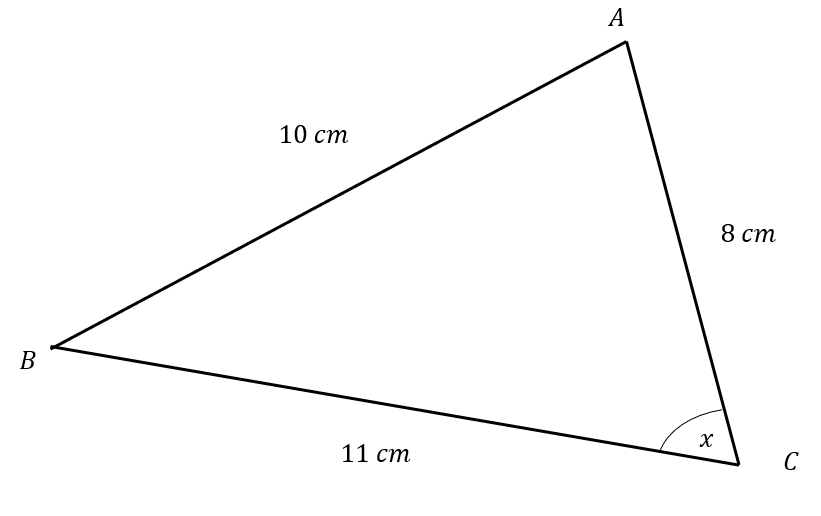
A triangle ABC is shown below:
Angle x is an acute angle.
Find the value of x.
Select the correct answer from the list below:
A: 58.3 \degree
B: 64.9 \degree
C: 55.7 \degree
D: 61.1 \degree
CORRECT ANSWER: B: 61.1 \degree
WORKED SOLUTION:
To calculate x we can use the cosine rule,
\text{cos}(A)=\dfrac{b^2+c^2-a^2}{2bc}
Hence substituting the values in,
\text{cos}(x)=\dfrac{11^2+8^2-10^2}{2(11)(8)}
Taking the inverse cosine of both sides,
x=\text{cos}^{-1} \bigg( \dfrac{85}{176} \bigg) =61.1\degree
Question 3
LEVEL 6
A triangle ABC is shown below:
Find the value of x.

Select the correct answer from the list below:
A: 5.62 cm
B: 14.42 cm
C: 24.51 cm
D: 4.95 cm
CORRECT ANSWER: D: 4.95 cm
WORKED SOLUTION:
To calculate x, we can use the cosine rule,
a^2 = b^2 + c^2 - 2bc \, \text{cos}(A)
Hence substituting the values in,
x^2 = 8^2 + 12^2 - 2 \times 8 \times 12 \times \text{cos}(35) = 24.5099...
Taking the square root of both sides, and only taking the positive value of x, since x represents a real physical length, we get
x = \sqrt{24.5099...} = 4.95 cm
Question 4
LEVEL 6
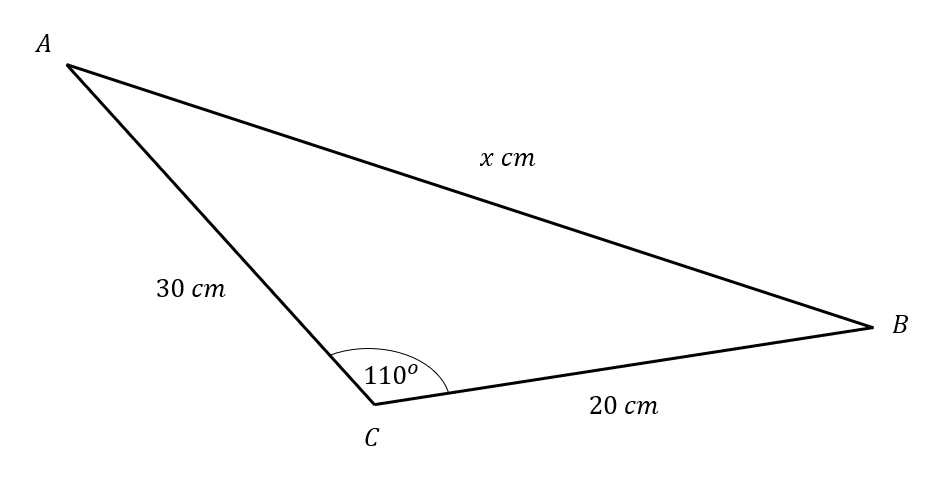
A triangle ABC is shown below:
Find the value of x.
Select the correct answer from the list below:
A: 41.36 cm
B: 36.06 cm
C: 29.83 cm
D: 45.56 cm
CORRECT ANSWER: A: 41.36 cm
WORKED SOLUTION:
To calculate x, we can use the cosine rule,
a^2 = b^2 + c^2 - 2bc \, \text{cos}(A)
Hence substituting the values in,
x^2 = 20^2 + 30^2 - 2 \times 20 \times 30 \times \text{cos}(110) = 1710.42...
Taking the square root of both sides, and only taking the positive value of x, since x represents a real physical length, we get
x = \sqrt{1710.42...} = 41.36 cm
Question 5
LEVEL 6
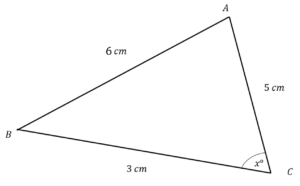
A triangle ABC is shown below:
Angle x is an acute angle.
Find the value of x.
Select the correct answer from the list below:
A: 85.66 \degree
B: 90.34 \degree
C: 93.82 \degree
D: 82.55 \degree
CORRECT ANSWER: C: 93.82 \degree
WORKED SOLUTION:
To calculate x we can use the cosine rule,
\text{cos}(A)=\dfrac{b^2+c^2-a^2}{2bc}
Hence substituting the values in,
\text{cos}(x)=\dfrac{3^2+5^2-6^2}{2(3)(5)}
Taking the inverse cosine of both sides,
x= \text{cos}^{-1} \bigg( \dfrac{-2}{30} \bigg) = 93.82 \degree
