Question 1
LEVEL 6
ABC is a triangle shown below.
Calculate the size of angle x, shown below.

Select the correct answer from the list below:
Answer: 51.32 \degree
B: 69.51 \degree
C: 53.95 \degree
D: 60.12 \degree
WORKED SOLUTION:
Use the rearranged cosine rule formula: \cos (A) = \dfrac{b^2 + c^2 - a^2}{2bc}
Substitute in the corresponding values:
\cos (x) = \dfrac{12^2 + 11^2 - 10^2}{2 \times 12 \times 11} = \dfrac{5}{8}Solve to find x:
x = {\cos}^{-1} (\frac{5}{8}) = 51.32 \degree (2 dp)
Question 2
LEVEL 6
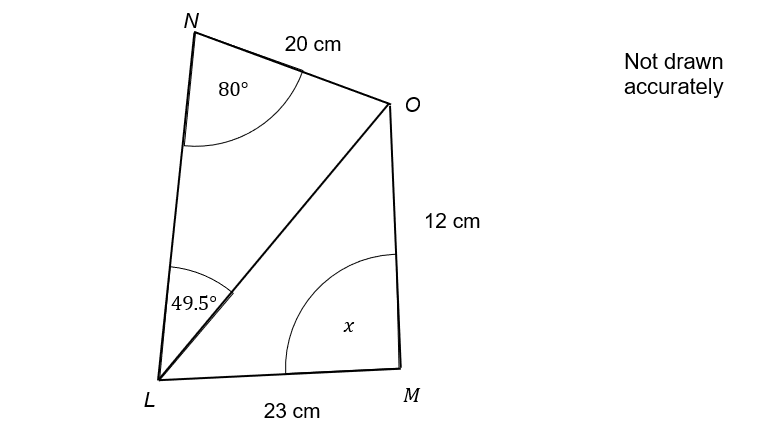
Two triangles are connected together to make the shape MLNO shown below.
Calculate \angle LMO shown on the diagram below.
Select the correct answer from the list below:
Answer: 89.78 \degree
B: 90.22 \degree
C: 86.78 \degree
D: 83.25 \degree
WORKED SOLUTION:
Calculate the length LO using the sine rule:
\dfrac{LO}{\sin(80)} = \dfrac{20}{\sin(49.5)}
LO = \dfrac{20 \sin(80)}{\sin(49.5)} = 25.9021...
Use the rearranged cosine rule formula to find x
\cos (x) = \dfrac{23^2 + 12^2 - (25.9021...)^2}{2 \times 23 \times 12} = 0.003765...x = {\cos}^{-1}(0.003765...) = 89.78 \degree (2 dp)
Question 3
LEVEL 6
Triangle ABC is shown below.
Calculate x shown on the diagram below.

Select the correct answer from the list below:
Answer: 8.46 m (2 dp)
B: 26.60 m
C: 15.43 m
D: 10.02 m
WORKED SOLUTION:
Use the sine rule formula:
\dfrac{x}{\sin(32)} = \dfrac{15}{\sin(70)}Then rearrange to find x:
x = \dfrac{15 \sin(32)}{\sin(70)} = 8.46 (2 dp)
Question 4
LEVEL 6
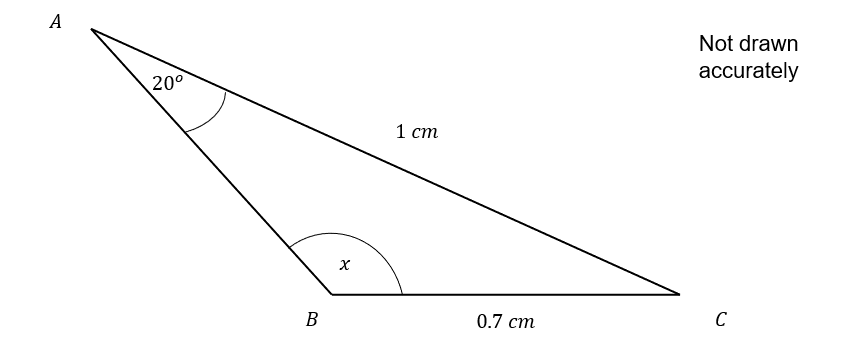
Triangle ABCD is shown on the diagram below.
Calculate the obtuse angle \angle ABC shown on the diagram below.
Select the correct answer from the list below:
Answer: 150.75 \degree
B: 29.25 \degree
C: 140.50 \degree
D: 39.50 \degree
WORKED SOLUTION:
Use the sine rule formula and rearrange to find x
\dfrac{\sin(x)}{1} = \dfrac{\sin(20)}{0.7}
\sin(x) = \dfrac{\sin(20)}{0.7} = 0.48860...
x = {\sin}^{-1}(0.48860...) = 29.2486...
This is not our final answer, since x is an obtuse angle.
Therefore we subtract our answer from 180 \degree to get the obtuse angle.
180 - 29.2486... = 150.75 \degree (2 dp)
Question 5
LEVEL 6
Two triangles are attached together to form the shape ABCD shown below.
Calculate the length of side CD marked on the diagram as x shown below.

Select the correct answer from the list below:
Answer: 11.46 m (2 dp)
B: 12.35 m
C: 10.79 m
D: 8.41 m
WORKED SOLUTION:
First, we need to find the length of BD.
Use the sine rule formula:
\dfrac{BD}{\sin(63)} = \dfrac{12}{\sin(44)}
BD = \dfrac{12 \sin(63)}{\sin(44)} = 15.3918...
Then use the cosine rule to find x:
x^2 = 11^2 + (15.3918...)^2 - 2 \times 11 \times (15.3918...) \cos(48)
x^2 = 131.3275...
x = \sqrt{131.3275...} = 11.46 m (2 dp)
