Question 1
LEVEL 8
PQ is a straight line with X as the midpoint.
PR is a straight line with M as the midpoint.
\overrightarrow{PX}=\textbf{a}
\overrightarrow{PM}=\textbf{b}
Find the vector \overrightarrow{QR} in terms of \mathbf{a} and \mathbf{b}.
Select the correct answer from the list below:
A: -2\textbf{a}+-2\textbf{b}
B: 2\textbf{a}-2\textbf{b}
C: 2\textbf{a}+2\textbf{b}
D: -2\textbf{a}+2\textbf{b}
CORRECT ANSWER: D: -2\textbf{a}+2\textbf{b}
WORKED SOLUTION:
\overrightarrow{QR} = - \overrightarrow{PQ} + \overrightarrow{PR}
\overrightarrow{PQ} = 2\overrightarrow{PX} = 2\mathbf{a}
\overrightarrow{PR} = 2\overrightarrow{PM} = 2\mathbf{b}
So,
\overrightarrow{QR} = -2\mathbf{a} + 2\mathbf{b}Question 2
LEVEL 8
PQ is a straight line with X as the midpoint.
PR is a straight line with M as the midpoint.
\overrightarrow{PQ}=\textbf{a}
\overrightarrow{PR}=\textbf{b}
Find the vector \overrightarrow{XM} in terms of \mathbf{a} and \mathbf{b}.
Select the correct answer from the list below:
A: \overrightarrow{XM}=-\dfrac{1}{2}\textbf{a}+\dfrac{1}{2}\textbf{b}
B: \overrightarrow{XM}=2\textbf{a}-\dfrac{1}{2}\textbf{b}
C: \overrightarrow{XM}=\textbf{a}+\dfrac{1}{2}\textbf{b}
D: \overrightarrow{XM}=\textbf{a}+\textbf{b}
CORRECT ANSWER: A: \overrightarrow{XM}=-\dfrac{1}{2}\textbf{a}+\dfrac{1}{2}\textbf{b}
WORKED SOLUTION:
\overrightarrow{XM} = - \overrightarrow{PX} + \overrightarrow{PM}
\overrightarrow{PX} = \dfrac{1}{2} \overrightarrow{PQ} = \dfrac{1}{2} \mathbf{a}
\overrightarrow{PM} = \dfrac{1}{2} \overrightarrow{PR} = \dfrac{1}{2} \mathbf{a}
So,
\overrightarrow{XM} = -\dfrac{1}{2}\textbf{a}+\dfrac{1}{2}\textbf{b}
\overrightarrow{XM}=-\dfrac{1}{2}\textbf{a}+\dfrac{1}{2}\textbf{b}
Question 3
LEVEL 8
\overrightarrow{QR}=5\overrightarrow{PS}
\overrightarrow{QX}=\dfrac{2}{3}\overrightarrow{XR}
Find \overrightarrow{SX} in terms of \mathbf{a} and \mathbf{b}.
Select the correct answer from the list below:
A: \textbf{a}+\textbf{b}
B: 2\textbf{a}+3\textbf{b}
C: -\textbf{a}-\textbf{b}
D: -2\textbf{a}+3\textbf{b}
CORRECT ANSWER: A: \textbf{a}+\textbf{b}
WORKED SOLUTION:
Looking at the diagram we’re given, we can see that there is no direct route from S to R, so we need to think of one:
\overrightarrow{SX}=\overrightarrow{SP}+\overrightarrow{PQ}+\overrightarrow{QX}
Well, we already have \overrightarrow{PQ} and can find \overrightarrow{SP} by multiplying \overrightarrow{PS} by -1, so we only need to find \overrightarrow{QX} .
We are given that \overrightarrow{QR}=5\overrightarrow{PS}, but we know \overrightarrow{PS}=\textbf{a}, so we can substitute that in: \overrightarrow{QR}=5\overrightarrow{PS}=5\textbf{a}.
Now, we need to figure out how much of 5a \overrightarrow{QX} is worth. Well, we are told that \overrightarrow{QX}=\dfrac{2}{3}\overrightarrow{XR} , so we can rewrite \overrightarrow{QR} as:
\overrightarrow{QR}=\overrightarrow{QX}+\overrightarrow{XR}
\overrightarrow{QR}=\dfrac{2}{3}\overrightarrow{XR} +\overrightarrow{XR}
\overrightarrow{QR}=\dfrac{2}{3}\overrightarrow{XR} +\dfrac{3}{3}\overrightarrow{XR}
\overrightarrow{QR}=\dfrac{5}{3}\overrightarrow{XR}
And now, because we know that \overrightarrow{QR} =5\textbf{a} we can substitute that in to the equation above.
5\textbf{a} =\dfrac{5}{3}\overrightarrow{XR}And now we can rearrange this to find \overrightarrow{XR} :
5\textbf{a} =\dfrac{5}{3}\overrightarrow{XR}
3\times5\textbf{a} =5\overrightarrow{XR}
15\textbf{a} =5\overrightarrow{XR}
15\textbf{a}\div5 =\overrightarrow{XR}
3\textbf{a} =\overrightarrow{XR}
Now that we have \overrightarrow{XR}, we can substitute this to find \overrightarrow{QX}
\overrightarrow{QX}=\dfrac{2}{3}\overrightarrow{XR}
\overrightarrow{QX}=\dfrac{2}{3}\times3\textbf{a}
\overrightarrow{QX}=2\textbf{a}
We now have all the vectors we need:
\overrightarrow{SP}=-\overrightarrow{SP}=-\textbf{a}
\overrightarrow{PQ}=\textbf{b}
\overrightarrow{QX}=2\textbf{a}
So now, we just need to add these up:
\overrightarrow{SX}=\overrightarrow{SP}+\overrightarrow{PQ}+\overrightarrow{QX}
\overrightarrow{SX}=-\textbf{a}+\textbf{b}+2\textbf{a}
\overrightarrow{SX}=\textbf{a}+\textbf{b}
Question 4
LEVEL 8
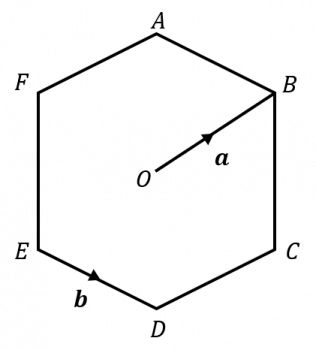
The diagram shows a hexagon ABCDEF, centre O, with vectors \overrightarrow{OB} = \mathbf{a} and \overrightarrow{ED} = \mathbf{b}.
Find an expression for the vector \overrightarrow{OA} in terms of \mathbf{a} and \mathbf{b}.
Select the correct answer from the list below:
A: \mathbf{a} + 2\mathbf{b}
B: \mathbf{a} - 2\mathbf{b}
C: 2\mathbf{a} + \mathbf{b}
D: 2\mathbf{a} - \mathbf{b}
CORRECT ANSWER: B: \mathbf{a} - 2\mathbf{b}
WORKED SOLUTION:
\overrightarrow{CA} = - \overrightarrow{OC} + \overrightarrow{OB} - \overrightarrow{AB}Then
\overrightarrow{CA} = - \mathbf{b} + \mathbf{a} - \mathbf{b} = \mathbf{a} - 2\mathbf{b}Question 5
LEVEL 8
\overrightarrow{ED}=6\textbf{a}-3\textbf{b}
\overrightarrow{DC}=4\textbf{b}
Given that AC forms a straight line such that AB:BC=5:1
\overrightarrow{BC}=\dfrac{1}{3}\overrightarrow{ED},
X is the midpoint of AD.
Find \overrightarrow{DX} in terms of \mathbf{a} and \mathbf{b}.
Select the correct answer from the list below:
A: -12\textbf{a}+10\textbf{b}
B: -6\textbf{a}+5\textbf{b}
C: 13\textbf{a}+7\textbf{b}
D: 5\textbf{a}+-9\textbf{b}
CORRECT ANSWER: B: -6\textbf{a}+5\textbf{b}
WORKED SOLUTION:
With vectors it is always got practice to write in any of the vectors we know or can deduce. For example, we can figure out \overrightarrow{BC} .
\overrightarrow{BC}=\dfrac{1}{3}\overrightarrow{ED}
\overrightarrow{BC}=\dfrac{1}{3}(6\textbf{a}-3\textbf{b})
\overrightarrow{BC}=2\textbf{a}-\textbf{b}
We are also told the ratio AB:BC = 5:1, meaning that \overrightarrow{AB} will be 5 lots of \overrightarrow{BC}
\overrightarrow{AB}=5\times \overrightarrow{BC}
\overrightarrow{AB}=5(2\textbf{a}-\textbf{b})
\overrightarrow{AB}=10\textbf{a}-5\textbf{b}
And now we can get on to the question. We need to find the vector \overrightarrow{DX}= , which will be half of \overrightarrow{DA} so we need to find this first.
We don’t have the vector \overrightarrow{DA} , but we can find it by putting other vectors we do know together.
The only problem we have here is that some of our vectors are the wrong way, so we need to multiply them by -1 to get them going in the right direction.
\overrightarrow{CB} =-\overrightarrow{BC}=-(2\textbf{a}-\textbf{b})=-2\textbf{a}+\textbf{b}
We can now substitute these into our previous “journey”
\overrightarrow{DA}=\overrightarrow{DC}+\overrightarrow{CB}+\overrightarrow{BA}
\overrightarrow{DA}=4\textbf{b}+(-2\textbf{a}+\textbf{b} )+(- 10\textbf{a}+5\textbf{b} )
\overrightarrow{DA}=4\textbf{b}-2\textbf{a}+\textbf{b} - 10\textbf{a}+5\textbf{b}
\overrightarrow{DA}=-12\textbf{a}+10\textbf{b}
The last thing we need to do now is, that because X is the midpoint of DA, is half the vector \overrightarrow{DA}=-12\textbf{a}+10\textbf{b}
\overrightarrow{DX}=\frac{1}{2}\overrightarrow{DA}
\overrightarrow{DX}=\frac{1}{2}(-12\textbf{a}+10\textbf{b})
\overrightarrow{DX}=-6\textbf{a}+5\textbf{b}








