Question 1
There are a total of 6 counters placed in a bag.
3 of the counters are blue and the other 3 are green.
On the probability scale below, mark with the a cross the probability that a green counter is taken out of the bag at random.

Select the correct answer from the list below:
A: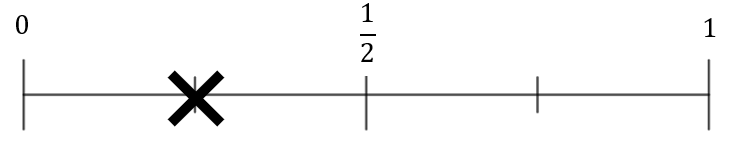
B: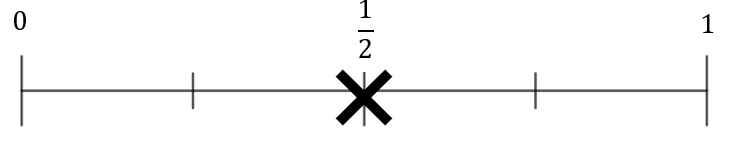
C:
D: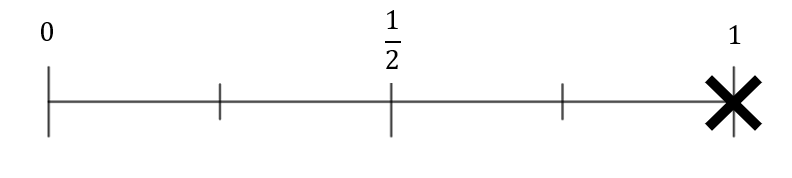
CORRECT ANSWER: B
WORKED SOLUTION:
The propbaility of an event happening can be expressed as fraction, percentage or decimal.
Here the probability is expressed as a fraction where the denominator of the fraction represents the total number of possible outcomes and the numerator represents the number of ways a certain event can occur.
In this case there is a total of 6 possible outcomes, as there are 6 counters that can be removed from the bag. Hence the denominator will be 6.
As there are 3 green counters in the bag, there are 3 different ways the event of picking a green counter can happen. Hence the numerator is 3.
So to express the probability of selecting a green counter at random is,
P(green)=\dfrac{3}{6}=\dfrac{1}{2}
Level 3
Question 2
A fair die is rolled and the number it lands on is recorded.
On the probability scale below, mark with the a cross the probability that the number is even.

Select the correct answer from the list below:
A: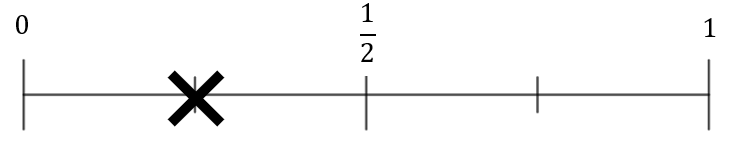
B: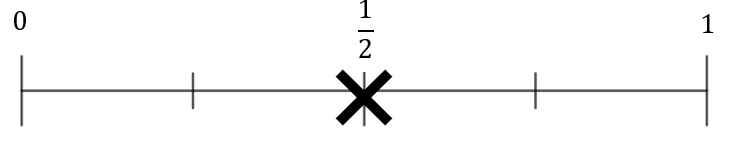
C:
D: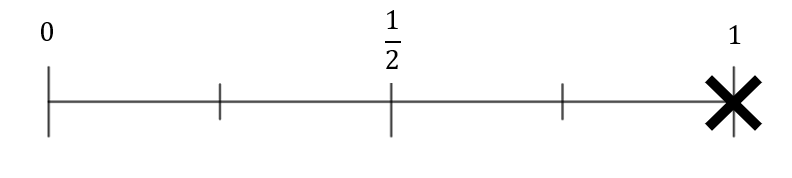
CORRECT ANSWER: B
WORKED SOLUTION:
The propbaility of an event happening can be expressed as fraction, percentage or decimal.
Here the probability is expressed as a fraction where the denominator of the fraction represents the total number of possible outcomes and the numerator represents the number of ways a certain event can occur.
In this case there is a total of 6 possible outcomes, as there are 6 scores possible when rolling a fair die. Hence the denominator will be 6.
As there are 3 even numbers between 1 and 6, there are 3 different ways the event of rolling an even number can happen. Hence the numerator is 3.
So to express the probability of rolling an even number is,
\dfrac{3}{6}=\dfrac{1}{2}
Level 3
Question 3
There are a total of 6 counters placed in a bag.
3 of the counters are blue and the other 3 are green.
On the probability scale below, mark with the a cross the probability that a orange counter is taken out of the bag at random.

Select the correct answer from the list below:
A: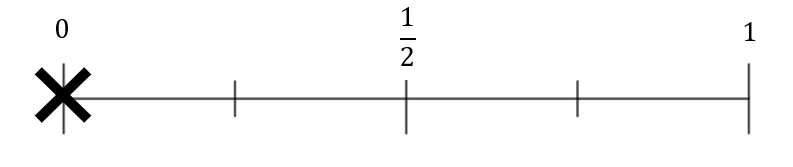
B: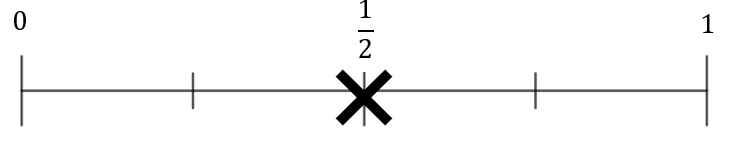
C:
D: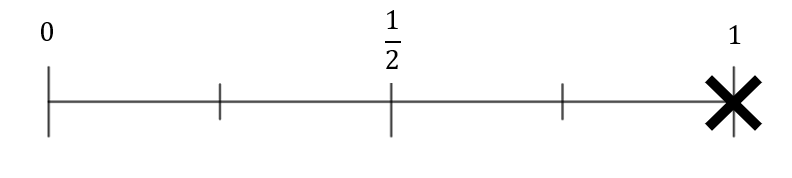
CORRECT ANSWER: A
WORKED SOLUTION:
The propbaility of an event happening can be expressed as fraction, percentage or decimal.
Here the probability is expressed as a fraction where the denominator of the fraction represents the total number of possible outcomes and the numerator represents the number of ways a certain event can occur.
In this case there is a total of 6 possible outcomes, as there are 6 counters that can be removed from the bag. Hence the denominator will be 6.
As there are zero orange counters in the bag, there are 0 different ways the event of picking an orange counter can happen. Hence the numerator is 0.
So to express the probability of selecting a orange counter at random is,
\dfrac{0}{6}=0
Level 3
Question 4
On the probability scale below, mark with the a cross the probability of achieving heads on an unbiased coin.

Select the correct answer from the list below:
A: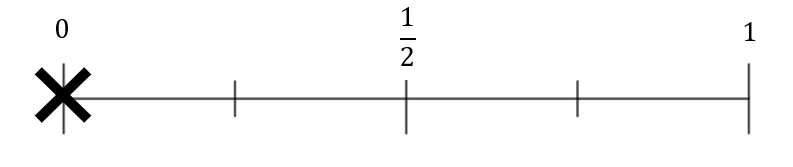
B: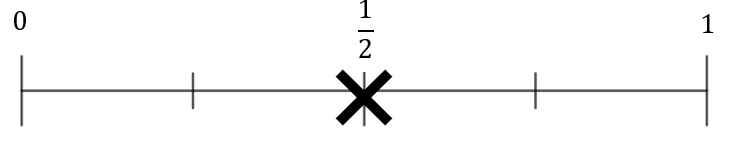
C:
D: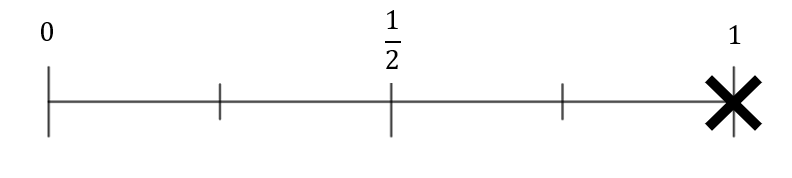
CORRECT ANSWER: B
WORKED SOLUTION:
The propbaility of an event happening can be expressed as fraction, percentage or decimal.
Here the probability is expressed as a fraction where the denominator of the fraction represents the total number of possible outcomes and the numerator represents the number of ways a certain event can occur.
In this case there is a total of 2 possible outcomes, either heads or tails. Hence the denominator will be 2.
As there is only one way to landed on a heads the numerator is 1.
So to express the probability of a coin flip landing on a heads is,
P(H)=\dfrac{1}{2}
Level 3
Question 5
On the probability scale below, mark with the a cross the probability that the sun will rise tomorrow.

Select the correct answer from the list below:
A: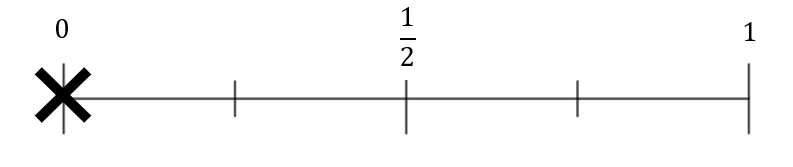
B: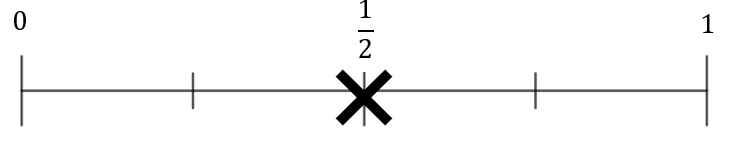
C:
D: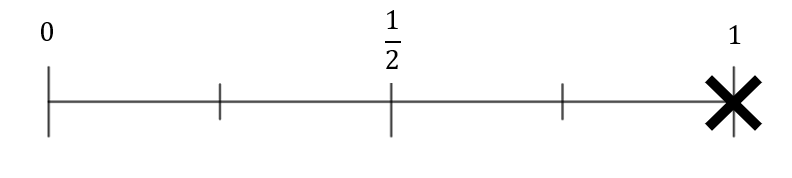
CORRECT ANSWER: D
WORKED SOLUTION:
The propbaility of an event happening can be expressed as fraction, percentage or decimal.
Here the probability is expressed as a fraction where the denominator of the fraction represents the total number of possible outcomes and the numerator represents the number of ways a certain event can occur.
In this case the event of the sunrise is certain so the probability is 1.
P(Sun rise)=\dfrac{1}{1}=1
Level 3
Question 6
The are 10 different colour counters are in a bag: blue, green and orange.
A counter is selected out from the bag at random.
The probability of pulling a green counter is \dfrac{2}{5}
The probability of pulling a blue counter is \dfrac{3}{10}
What is the probability of pulling an orange counter?
Select the correct answer from the list below:
A: \dfrac{1}{5}
B: \dfrac{1}{3}
C: \dfrac{3}{10}
D: \dfrac{2}{5}
CORRECT ANSWER: C: \dfrac{3}{10}
WORKED SOLUTION:
The propbaility of an event happening can be expressed as fraction, percentage or decimal.
Here the probability is expressed as a fraction where the denominator of the fraction represents the total number of possible outcomes and the numerator represents the number of ways a certain event can occur.
In this case there is a total of 10 possible outcomes, as there are 10 counters that can be removed from the bag. Hence the denominator will be 10.
There are 3 blue counters in the bag, and there are \dfrac{2}{5}=\dfrac{4}{10}, so 4 green counters in the bag.
Hence there are only three counters left unaccounted for and these must be orange. Hence the numerator is 3.
So to express the probability of selecting a orange counter at random is,
P(orange)= 1-\dfrac{3}{10}-\dfrac{4}{10}= \dfrac{3}{10}
Level 3
Question 7
A bag contains only red, blue, green, and yellow marbles. Use the table below to find the probability of picking a blue marble.
Select the correct answer from the list below:
A: 0.9
B: 0.1
C: 1
D: 0.024
CORRECT ANSWER: B: 0.1
WORKED SOLUTION:
We don’t know what the probability of getting a blue marble is, so let’s call it x.
We know that all probabilities have to add up to 1, so we can say,
0.2+x+0.3+0.4=1
x+0.9=1
x=1-0.9 =0.1
Level 4
Question 8
Ezra spins two spinner number 1 to 5 and records the sum of the two values each spinner lands on. What is the probability that of Harry recording a score greater than 8.

Select the correct answer from the list below:
A: 0.12
B: 0.2
C: 0.3
D: 0.\dot{3}
CORRECT ANSWER: A: 0.12
WORKED SOLUTION:
For this type of question it is best to draw sample space diagram. This looks like a two-way table that has all possible outcomes,
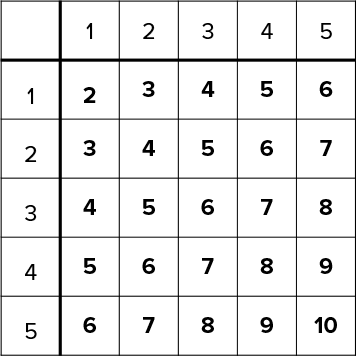
Now to find the probability of recording a score of more than 8 requires counting the number of scores bigger than 8 which turns out to be 3 (i.e. 9,9,10). So there are 3 events out of a total of 25 possible outcomes that satisfy the condition. So the probability is,
\text{P(more than 8)} =\dfrac{3}{25}
Level 4
Question 9
A box contains only red, blue, green, and yellow marbles.
When picking marbles you are twice as likely to pick a red marble than a yellow marble, four times more likely to pick a blue than a red, and half as likely to choose a green than a blue.
Find the probability of picking a green marble.
Select the correct answer from the list below:
A: \dfrac{1}{15}
B: \dfrac{1}{5}
C: \dfrac{4}{15}
D: \dfrac{3}{17}
CORRECT ANSWER: C: \dfrac{4}{15}
WORKED SOLUTION:
There is a lot to take in, so it can be helpful to draw/write something to help us, like a table.
The way the question tells us our chances of picking a marble starts with yellow, but because we don’t know what it is we can call it x.
Then we are told that we are twice as likely to pick a red than a yellow, so this will be two times the chance of picking a yellow, x\times 2=2x.
Then we are told that we are four times as likely to pick a blue than a red, so this will be four times the chance of picking a red, 2x\times 4=8x.
Finally, we are told that we are half as likely to pick a green marble than a blue marble, so this will be half the chance of picking a blue marble, 8x\div2=4x.
Now, we know that all probabilities have to add up to 1, so we can say
2x+8x+4x+x=1
15x=1
x=\dfrac{1}{15}
Now, we can find the probabilities by substituting in our value of x
So, the probability of getting a green marble is \dfrac{4}{15}.
Level 4
Question 10
Jacques is rolling two fair six-sided dice.
Find the probability that the sum of the two dice will be less than 7.
Select the correct answer from the list below:
A: \dfrac{1}{36}
B: \dfrac{1}{6}
C: \dfrac{7}{12}
D: \dfrac{5}{12}
CORRECT ANSWER: D: \dfrac{5}{12}
WORKED SOLUTION:
To find a probability we need to do:
\text{Probability }=\dfrac{\text{Number of Outcomes We Want}}{\text{Total Number of Possible Outcomes}}
The easiest way to see the outcomes we want is to draw a sample space of all possible outcomes.
Now that we have this, we can count the total number outcomes to be 36. Now, all we need to do is count how many outcomes we want (numbers less than 7).
So, our probability will be:
\text{Probability }=\dfrac{\text{Number of Outcomes We Want}}{\text{Total Number of Possible Outcomes}}=\dfrac{15}{36}=\dfrac{5}{12}
Level 4
Question 11
Given a standard deck of 52 cards, what is the probability of selecting a red 3 and then a black picture card without replacement?
Select the correct answer from the list below:
A: \dfrac{69}{442}
B: \dfrac{3}{1352}
C: \dfrac{3}{676}
D: \dfrac{1}{221}
CORRECT ANSWER: D: \frac{1}{221}
WORKED SOLUTION:
To find a probability we need to do:
\text{Probability }=\dfrac{\text{Number of Outcomes We Want}}{\text{Total Number of Possible Outcomes}}
The easiest way to see the outcomes we want is to draw a sample space of all possible outcomes.
So, in total we have 52 outcomes. To start off with, we need to select a red 3.
The probability of getting a red 3 is therefore
\text{Probability }=\dfrac{\text{Number of Outcomes We Want}}{\text{Total Number of Possible Outcomes}}=\dfrac{2}{52}=\dfrac{1}{26}
And now we need to look at the probability of selecting a black picture card (J,Q, and K).
So, there are 6 outcomes we want here. But we need to be careful, because we are not replacing the red 3 from before, our total number of possible outcomes goes down to 51. Our probability will be
\text{Probability }=\dfrac{\text{Number of Outcomes We Want}}{\text{Total Number of Possible Outcomes}}=\dfrac{6}{51}
Finally, to find the probability of selecting a red 3 and then a black picture card, we just need to multiply the probabilities.
\dfrac{1}{26}\times \dfrac{6}{51}=\dfrac{6}{1326}=\dfrac{1}{221}
Level 4














