Question 1
James is taking part in darts competition where he throws two darts.
- His chance of hitting a bullseye on his first throw 0.65.
- If he hits a bullseye on his first throw, he has a 0.8 chance of hitting it again on his second throw.
- If he misses his first throw, he has a 0.8 chance of missing on his second throw.
Complete the tree diagram to find the probability that James hits at least one bullseye.
Select the correct answer from the list below:
A: 0.72
B: 0.8
C: 0.2
D: 0.67
CORRECT ANSWER: A: 0.72
WORKED SOLUTION:
- We are told that the probability of James hitting a bullseye on his first throw is 0.65, so his probability of missing will be 1-0.65=0.35.
- Following a “Hit”,we are told that this time he will have a 0.8 chance of hitting another bullseye, so his chance of missing will be 1-0.8=0.2.
- Similarly, following a “Miss”, we are told that his chance of missing will be 0.8, so his chance of hitting will be 1-0.8=0.2.
And now, we can find the probabilities by multiplying along the branches.
We can do a little check by adding up these probabilities, and they should add up to 1.
0.52+0.13+0.07+0.28=1
Finally, we want to know his probability of hitting AT LEAST one bullseye, meaning we want to follow two branches with at least one hit.
And now, all we need to do is add these
0.52+0.13+0.07=0.72
Level 6
Question 2
There are 15 coloured marbles in a bag. 7 of them are blue and the rest are orange.
One marble is taken out at random. Without replacing the first marble a second marble is taken out at random.
What is the probability that the two marbles selected are different colours.
Select the correct answer from the list below:
A: \dfrac{16}{225}
B: \dfrac{8}{15}
C: \dfrac{5}{33}
D: \dfrac{9}{22}
CORRECT ANSWER: B: \dfrac{8}{15}
WORKED SOLUTION:
To simplify this problem we can represent the probabilities using a tree diagram.
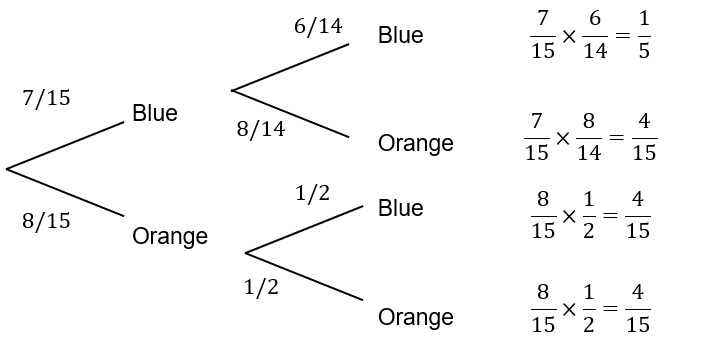
Here we have filled out the probabilities being careful to remember that the first marble is not replaced so the denominator has to be reduced by one.
There are two ways of selecting two marbles that are different colours. So the probability is,
P(different colours) = \dfrac{4}{15} + \dfrac{4}{15} = \dfrac{8}{15}
Level 8
Question 3
There are 12 volleyballs in a kit bag. 5 of them are red and the rest are green.
Two volleyballs are taken out at random with replacement. What is the probability of the two volleyballs being the same colour?
Select the correct answer from the list below:
A: \dfrac{35}{66}
B: \dfrac{31}{66}
C: \dfrac{5}{33}
D: \dfrac{9}{22}
CORRECT ANSWER: B: \dfrac{31}{66}
WORKED SOLUTION:
To simplify this problem we can represent the probabilities using a tree diagram.
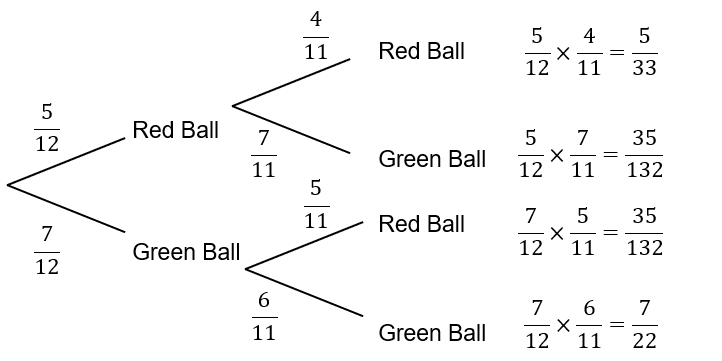
Here we have filled out the probabilities being careful to remember that the first ball is not replaced so the denominator as to be reduced by one.
There are two ways of selecting two balls of the same colour. So the probability is,
P(Same colour) = \dfrac{5}{33} + \dfrac{7}{22} = \dfrac{31}{66}
Level 8
Question 4
Charlotte is playing a game of pool and gets 2 free shots after her opponent pots the white ball.
The probability of Charlotte potting a ball on the first shot is 0.65.
If she is successful in potting a ball on the first shot then the likelihood of potting another on the second shot is 0.85.
However if she miss the first shot then the probability of her successfully potting a ball on the second attempt drops to 0.55.
By constructing a tree diagram work out the probability that Charlotte plot exactly one ball from the 2 free shots.
Select the correct answer from the list below:
A: 0.22
B: 0.48
C: 0.65
D: 0.29
CORRECT ANSWER: D: 0.29
WORKED SOLUTION:
To simplify this problem we can represent the probabilities using a tree diagram.
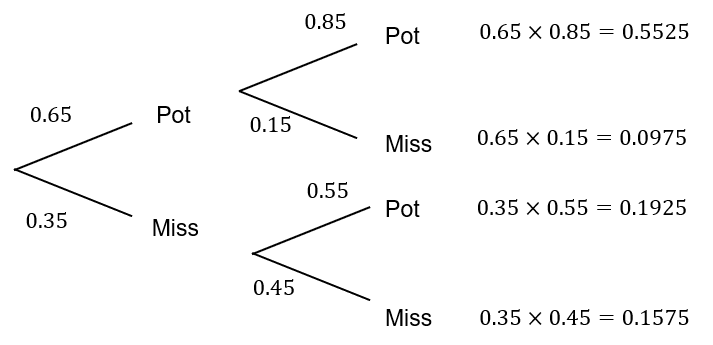
Here we have filled out the probabilities being careful to place the different probability on the secondary branches given the outcome of the first shot.
There are two ways of Charlotte potting one ball from the 2 shots. Either she misses the first shot and successfully pots a ball on the second or she pots a ball with the first shot then misses the second.
These two outcomes are represented by the middle branches of the diagram
P(\text{Pots one ball}) = 0.1925 + 0.0975 = 0.29
Level 8
Question 5
LEVEL 8
There are 20 coloured sweets in a packet. 11 of them are red and the rest are black.
One sweet is taken out at random. Without replacing the first sweet, a second sweet is taken out at random.
What is the probability that at least one of the two sweets selected are black?
Select the correct answer from the list below:
A: \dfrac{270}{380}
B: \dfrac{110}{380}
C: \dfrac{290}{400}
D: \dfrac{72}{380}
CORRECT ANSWER: A: \dfrac{270}{380}
WORKED SOLUTION:
To simplify this problem we can represent the probabilities using a tree diagram.
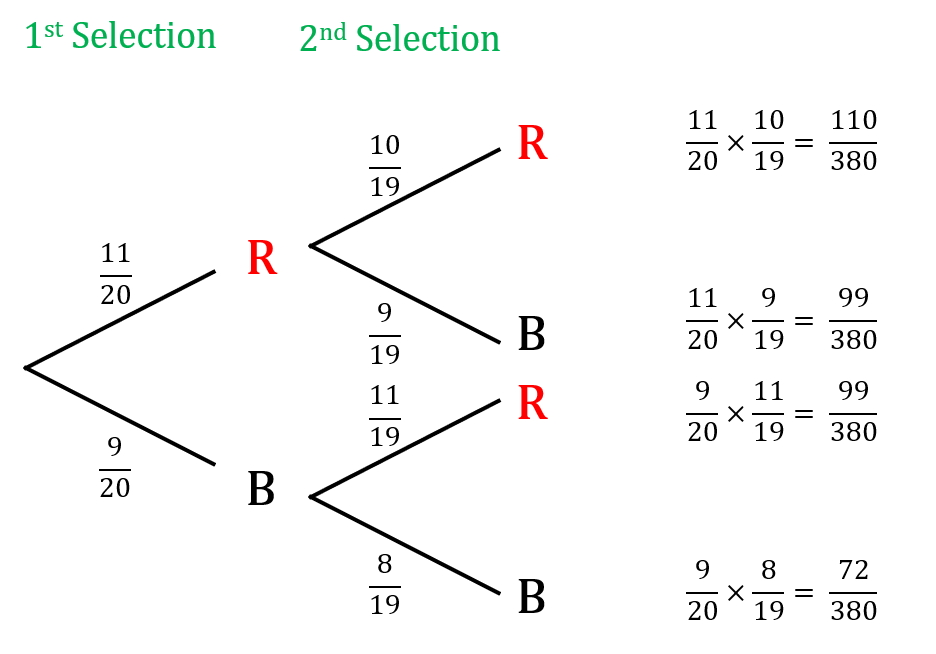
There are three ways of choosing at least one black sweet, red then black or black then red or black then black.
To calculate this, we can add up the probabilities that we calculated on the right, or equivalently we can subtract the probability of only getting red sweets, from 1.
We get
P(\text{At least one black sweet}) = 1 - \dfrac{110}{380} = \dfrac{270}{380}



