05. Venn Diagrams (Foundation)

Question 1

Draw a Venn diagram for the following information:

\xi=\{1\leq x\leq15 \}

A=\{\text{Odd Numbers}\}

B=\{ \text{Prime Numbers}\}

Select the correct answer from the list below:

A:

B:

C:

D:

CORRECT ANSWER:   B

WORKED SOLUTION:

Whenever given sets in words, it is always easiest to start by writing out everything that is in that set. It is also important to start with the universal set (\xi).

We start with the universal set because it tells us everything that is going to be in our other sets. If we didn’t know our biggest number here, the sets A and B would go on forever.

A=\{\text{Odd Numbers}\}=\{1,3,5,7,9,11,13,15\}
B=\{ \text{Prime Numbers}\}={2,3,5,7,11,13}

So, to start, we need to draw our universal set (with a rectangle) and then two overlapping circles to represent sets A and B.

And now we can start putting the numbers in. It doesn’t matter which set you start with, but it can be easiest to start with the smallest, in this case it is B. Starting with the 2, we can see that it isn’t in A, so must only be in B.

Next we have a 3, which we can see is in A as well, so this will go in the intersection (middle).

Following these steps through, set B will look like this:

And now, everything left in set A must only be in the A part of the Venn diagram.

Last, but not least, everything else left in the universal set will go on the outside.

A little check you can do is counting all the numbers in your Venn diagram and comparing this to the universal set you were given. If they don’t match up, something has gone missing!

Level 4

Question 2

Draw a Venn diagram for the following information:

\xi=\{\text{Odd Numbers Between 0 and 30}\}

A=\{\text{Multiples of 3 }\}

B=\{ \text{Multiples of 5 }\}

Select the correct answer from the list below:

A:

B:

C:

D:

CORRECT ANSWER:   C

WORKED SOLUTION:

Whenever given sets in words, it is always easiest to start by writing out everything that is in that set. It is also important to start with the universal set (\xi).

We start with the universal set because it tells us everything that is going to be in our other sets. If we didn’t know our biggest number here, the sets A and B would go on forever.

Note how we don’t have any even multiples of 3 in A, because there aren’t any even numbers in \xi.

Note how we don’t have 10 or 20 in B, because they aren’t in \xi

So, to start, we need to draw our universal set (with a rectangle) and then two overlapping circles to represent sets A and B.

And now we can start putting the numbers in. It doesn’t matter which set you start with, but it can be easiest to start with the smallest, in this case it is B. Starting with the 5, we can see that it isn’t in A, so must only be in B.

Next, we have a 15, which we can see is in A as well, so this will go in the intersection (middle).

Following these steps through, set B will look like this:

And now, everything left in set A must only be in the A part of the Venn diagram.

Last, but not least, everything else left in the universal set will go on the outside.

A little check you can do is counting all the numbers in your Venn diagram and comparing this to the universal set you were given. If they don’t match up, something has gone missing!

Level 4

Question 3

Jeremiah collected data on 50 people’s gaming habits. X is the set of people that use an X-Box and Y is the set of people that use a Playstation.

Complete the Venn diagram shown below:

Select the correct answer from the list below:

A: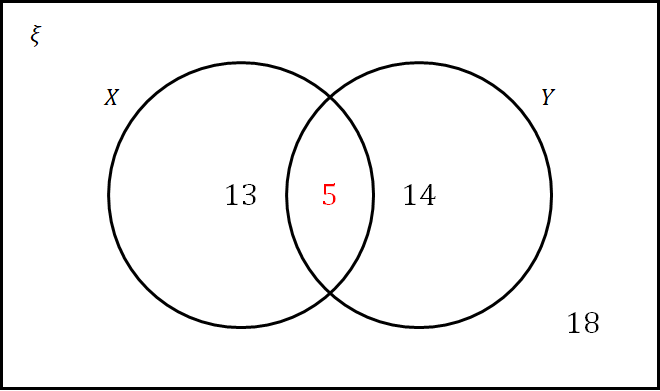

B: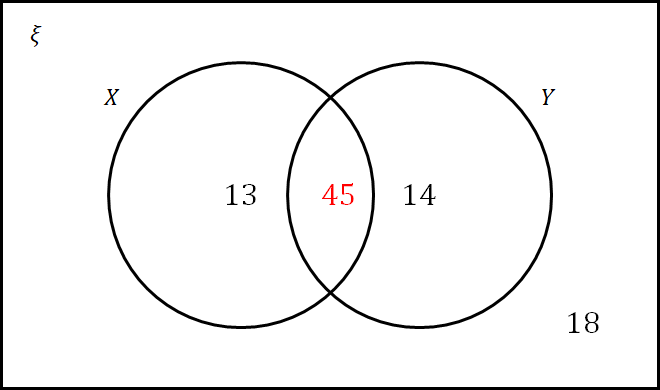

C: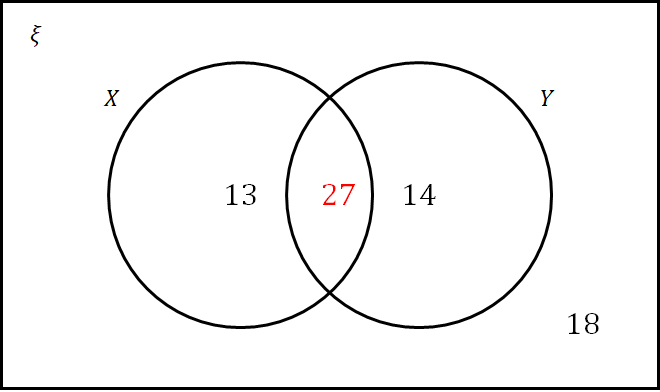

D: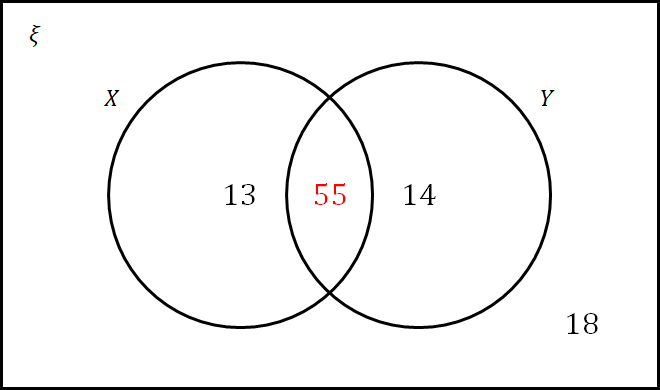

CORRECT ANSWER:   A

WORKED SOLUTION:

From our Venn diagram we have the information for 13+14+18=45 people. o, to find our missing part of the Venn diagram we do 50-45=5. So, there are going to be 5 people in the intersection.

Level 4

Question 4

50 Students study at university.

20 students study only maths

5 students study both maths and English

4 students study neither maths or English

x students study English only

Find the value of x

Select the correct answer from the list below:

A:  17

B:  19

C:  21

D:  23

CORRECT ANSWER:   C:  21

WORKED SOLUTION:

Students that only study English x=50-4-5-20=21.

Level 4

Question 5

400 people take part in a study to determine the favourite type of fruit tea.

300 people people select apricot (A)

20 people select mango only (M)

12 people do not choose either mango or apricot.

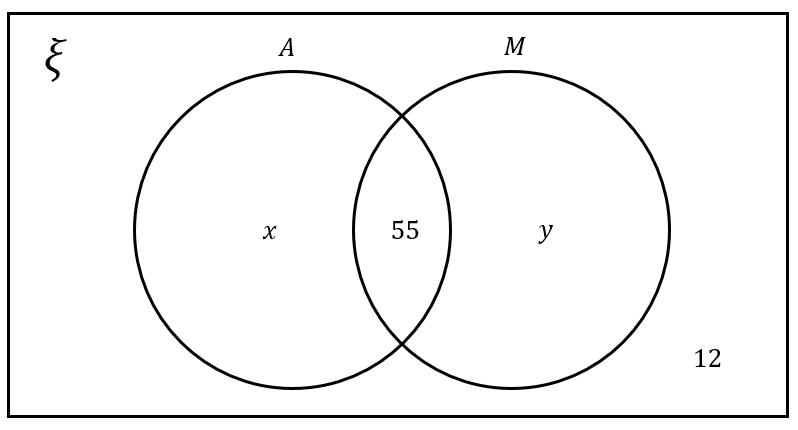
Find the value of x

Select the correct answer from the list below:

A: 25

B: 45

C: 145

D:  245

CORRECT ANSWER:   D:  245

WORKED SOLUTION:

People that only chose apricot only x=300-55=245.

Level 4