25. Graphical Inequalities

Question 1

LEVEL 6

Find the region, R, of the graph that satisfies the inequality $y\leq2x+3$.

Select the correct answer from the list below:

A:

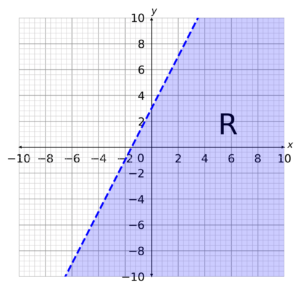
B:

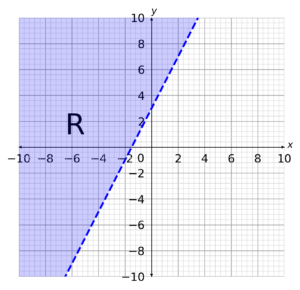
C:

D:

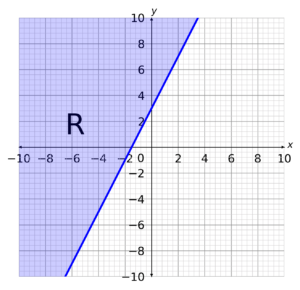
CORRECT ANSWER:    C

WORKED SOLUTION:

Start by thinking of $y\leq2x+3$ as an equation instead, $y=2x+3$. We know how to draw this.

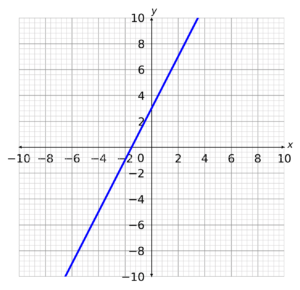
And now, because it is $\leq$, we just need to shade the region beneath the graph and label it R. (We also need to remember that because it has “equals” it is a solid line).

To check you have the right region, you can choose a point and put those values of $x$ and $y$ into the inequality.

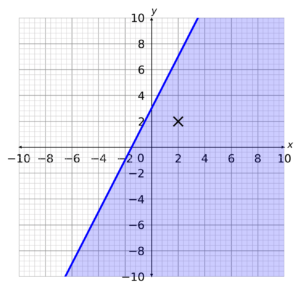
Try $(2,2)$
$x=2 \textrm{ and } y=2$
$y\leq2x+3$

$2\leq2\times2+3$
$2\leq4+3$
$2\leq7$

Which is true, so we have the correct region.

Question 2

LEVEL 6

Which inequality is described by the shaded region below?

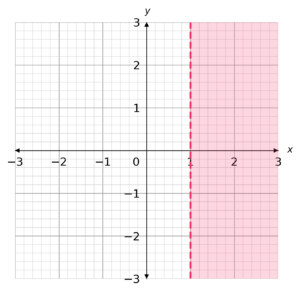
Select the correct answer from the list below:

A: $x>1$

B: $x<1$

C: $y<1$

D: $x\leq1$

CORRECT ANSWER:A: $x>1$

WORKED SOLUTION:

The line is dashed, so we know that the answer must have a strict inequality, < or >.

The equation of the line is $x = 1$, since is cuts through the $x$-axis at $1$, so the answer must be $x>1$ or $x<1$.

The shaded area is to the right of the line, that includes $x$ values greater than $1$.

So the answer must be $x>1$.

Question 3

LEVEL 6

Which inequality is described by the shaded region below?

Select the correct answer from the list below:

A: $x>1$

B: $x\geq1$

C: $y<1$

D: $x\leq1$

CORRECT ANSWER: B: $x\geq1$

WORKED SOLUTION:

The line is solid, so we know that the answer must have an inclusive inequality, $\leq$ or $\geq$.

The equation of the line is $x = 1$, since is cuts through the $x$-axis at $1$, so the answer must be $x \geq 1$ or $x \leq 1$.

The shaded area is to the right of the line, that includes $x$ values greater than or equal to $1$.

So the answer must be $x \geq 1$.

Question 4

LEVEL 6

Which inequality is described by the shaded region below?

Select the correct answer from the list below:

A: $y>3$

B: $y\leq3$

C: $y\geq3$

D: $y>3$

CORRECT ANSWER: C: $y\geq3$

WORKED SOLUTION:

The line is solid, so we know that the answer must have an inclusive inequality, $\leq$ or $\geq$.

The equation of the line is $y = 3$, since is cuts through the $y$-axis at $3$, so the answer must be $y \geq 3$ or $y \leq 3$.

The shaded area is above the line, that includes $y$ values greater than or equal to $3$.

So the answer must be $y\geq3$.

Question 5

LEVEL 6

Which inequality is described by the shaded region below?

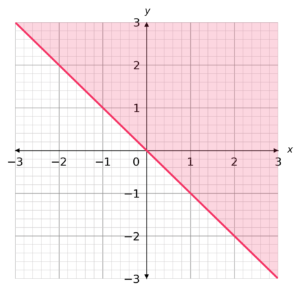
Select the correct answer from the list below:

A: $x+y>0$

B: $x+y\geq0$

C: $x-y\geq0$

D: $x+y\leq0$

CORRECT ANSWER:B: $x+y\geq0$

WORKED SOLUTION:

The line is solid, so we know that the answer must have an inclusive inequality, $\leq$ or $\geq$.

The equation of the line is $y = - x$ which is equivalent to $y + x = 0$, so the answer must be B,C or D..

The shaded area is above the line, that includes values of $x + y$  greater than or equal to $0$.

So the answer must be $x+y\geq0$.

Question 6

LEVEL 6

Which set of inequalities is described by the shaded region below?

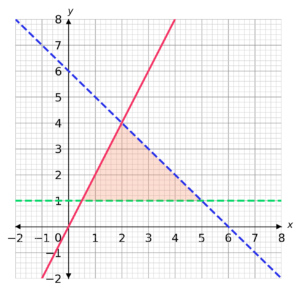
Select the correct answer from the list below:

A: $y - 2x \geq 0, \,\, y >1, \,\, y + x - 6 > 0$

B: $y - 2x \leq 0, \,\, y >1, \,\, y + x - 6 < 0$

C: $y - 2x <0, \,\, y \geq 1, \,\, y + x - 6 \leq 0$

D: $y - 2x \leq 0, \,\, x >1, \,\, y + x - 6 < 0$

CORRECT ANSWER: B: $y - 2x \leq 0, \,\, y >1, \,\, y + x - 6 < 0$

WORKED SOLUTION:

The equation of the red line is $y = 2x$ which is equivalent to $y-2x=0$.

The line is solid, so we must have an inclusive inequality, $\leq$ or $\geq$.

The shaded area is below the line, that includes the values of $y-2x$ less than or equal to $0$.

So we have $y - 2x \leq 0$.

The equation of the blue line is $y = - x + 6$ which is equivalent to $y+x - 6=0$.

The line is dashed, so we must have a strict inequality, $<$ or $>$.

The shaded area is below the line, that includes the values of $y+x-6$ less than $0$.

So we have $y + x - 6 < 0$.

The equation of the green line is $y = 1$.

The line is dashed, so we must have a strict inequality, $<$ or $>$.

The shaded area is above the line, that includes the values of $y$ greater than $1$.

So we have $y > 1$.

So our answer is B.

Question 7

LEVEL 6

Find the shaded region for the following inequalities:

Select the correct answer from the list below:

A:

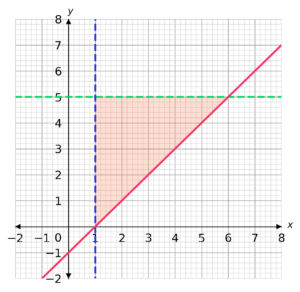
B:

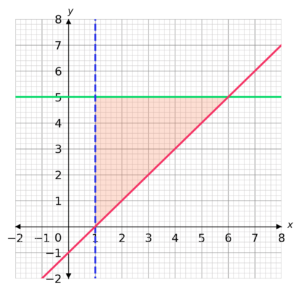
C:

D:

CORRECT ANSWER: D

WORKED SOLUTION:

$x=1$ is a vertical line passing through $1$ on the $x$ axis.

Since we want $x \geq 1$, we want a solid line and the shaded area will be to the right of the line, where the values of $x$ are greater than or equal to $1$.

$y=5$ is a horizontal line passing through $5$ on the $y$ axis.

Since we want $y \leq 5$, we want a solid line and the shaded area will be below the line, where the values of $y$ are less than or equal to $5$.

$y-x+1=0$ is equivalent to$y = x - 1$, which is a line passing through $-1$ on the $y$ axis, with a gradient of $1$.

Since we want $y-x+1 >0$ we want a dashed line and the shaded area will be above the line, where the values of $y-x+1$ are greater than or equal to $0$.

Therefore our answer is D.