Question 1
LEVEL 4
Given the statement,
5(4x−5)−2(5?+9) \equiv Ax−43
where A is an integer,, choose the correct statement from the list below:
A: The statement is false
B: The statement is true, and A = 20
C: The statement is true, and A = 10
D: The statement is true, and A = 15
CORRECT ANSWER: C: The statement is true, and A = 10
WORKED SOLUTION:
First expand the brackets on the equation,
5(4x−5)−2(5?+9)=20x-25-10x-18
Then group together similar terms,
20x-25-10x-18=10x-43
Hence comparing this to the RHS of the identity in the question
10x-43 \equiv Ax−43
We can see the value of A is 10 by matching the terms either side of the identity, and so the statement is true.
Question 2
LEVEL 4
Given the statement,
(4x−5)^2−(2x+1)^2 \equiv 12x^2 -44x+B
where B is an integer, choose the correct statement from the list below:
A: The statement is false
B: The statement is true, and B = 24
C: The statement is true, and B = 16
D: The statement is true, and B = 8
CORRECT ANSWER: B: The statement is true, and B = 24
WORKED SOLUTION:
First expand the brackets on the equation,
(4x−5)^2−(2x+1)^2 =(4x−5)(4x−5)-(2x+1)(2x+1)=(16x^2-40x+25)-(4x^2+4x+1)
Then group together similar terms,
(16x^2-40x+25)-(4x^2+4x+1)=12x^2-44x+24
Hence comparing this to the RHS of the identity in the question
12x^2-44x+24 \equiv 12x^2 -44x+B
We can see the value of B is 24 by matching the terms either side of the identity, and so the statement is true.
Question 3
LEVEL 4
Given the statement,
(2n+3)^2−(3n+2) \equiv 4n^2 +Cn+8
where C is an integer, choose the correct statement from the list below:
A: The statement is false
B: The statement is true, and C = 15
C: The statement is true, and C = 9
D: The statement is true, and C = 6
CORRECT ANSWER: A: The statement is false
WORKED SOLUTION:
First expand the brackets on the equation,
(2n+3)^2−(3n+2) =(2n+3)(2n+3)-(3n+2)=(4n^2+12n+9)-(3n+2)
Then group togther similar terms,
(4n^2+12n+9)-(3n+2)=4n^2+9n+7
Hence comparing this to the RHS of the identity in the question
4n^2+9n+7 \equiv 4n^2 +Cn+8
We can see the constant term is 7 on the LHS, but 8 on the RHS. Therefore the statement is false.
Question 4
LEVEL 4
Which of the following always represents an even number
A: 4n+1
B: 2n+1
C: 2n
D: n
CORRECT ANSWER: C: 2n
WORKED SOLUTION:
2n, where n is a positive integer, is always even, since the first even number counting up from 1 is 2, and then every other integer is even.
Question 5
LEVEL 4
Which of the following always represents an odd number
A: 5n+1
B: 2n+1
C: 2n
D: n
CORRECT ANSWER: B: 2n+1
WORKED SOLUTION:
2n, where n is a positive integer, is always even, so 2n+1 which is 1 greater than an even number, is always odd.
Question 6
LEVEL 4
Given the image
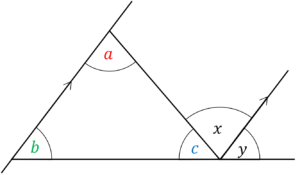
Where A is an integer.
Select the statement from the list below that is always true:
A: c+y = 90^\circ
B: a+c+y = 180^\circ
C: a=y
D: a+b+x = 180^\circ
CORRECT ANSWER: B: a+c+y = 180^\circ
WORKED SOLUTION:
We know that a = x, since they are alternate angles.
Also, we know that c+x+y = 180^\circ, since angles on a straight line add up to 180^\circ.
Substitute in a=x into the latter equation, to get
a+c+y = 180^\circ.
