3. June 18 Higher Paper 3

NOTE: Q1-8 are the same as Q19-26 on June 18 Foundation Paper 3

(DOESN’T NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)

 

Q21 – (Marks swapped compared to edexcel paper – was 3 for (a) then 2 for (b) – now 2 for (a) then 3 for (b))

---

Question 1

The scatter diagram shows information about $10$ boys.

It shows the age of each boy and the best distance he jumps in a long jump competition.

 

Question 1(a) [1 mark]

What type of correlation does the scatter graph show?

 

Answer type: Multiple choice type 1

A: Positive correlation

B: Negative correlation

C: No correlation

 

ANSWER: A

 

 

 

Question 1(b) [1 mark]

Adam is $15$ years old.

His best long jump is $6.1$ m

Which statement correctly describes the point representing this information?

 

Answer type: Multiple choice type 1

A: The point is an outlier

B: The point is in line with the trend of the other points

 

ANSWER: A

 

 

 

Question 1(c) [1 mark]

Mark is $19$ years old.

Mark says

“The scatter diagram shows that I should jump at least $6.5$ m on a long jump”

 

Choose the correct statement regarding his comment.

 

Answer type: Multiple choice type 1

A: The point would be outside the range of the scatter diagram

B: The point would be inside the range of the scatter diagram

 

ANSWER: A

 

---

 

Question 2 [2 marks]

Expand and simplify $4(r+2) - 3(1-3r)$

 

Answer type: Multiple choice type 1

A: $13r + 5$

B: $5 - 5r$

C: $13r - 5$

D: $5r - 5$

 

ANSWER: A

WORKING:

$4(r+2) - 3(1-3r)$

$= 4r + 8 - 3 + 9r$

$= 13r + 5$

 

---

 

Question 3 [2 marks]

Here is a triangle drawn on a centimetre grid.

Calculate the length of one side of a square that is equal in area to the triangle above.

 

Answer type: Simple text answer

ANSWER: 3 cm

WORKING:

Area of triangle $= \dfrac{1}{2} \times 6 \times 3 = 9$ cm$^2$

Area of square $= 9$ cm$^2$

Side length of square $= \sqrt{9} = 3$ cm

 

---

 

Question 4

When a biased $4$ sided spinner is spun once, the probability that it will land on $1$ is $0.40$

The biased spinner is spun twice.

Abdul starts drawing the probability tree diagram.

 

Choose the correctly completed probability tree diagram based on this information.

 

Answer type: Multiple choice type 1

A:

B:

C:

D:

 

ANSWER: A

WORKING:

Probability of landing on $1 = 0.4$

Probability of NOT landing on $1 = 1 - 0.4 = 0.6$

 

---

 

Question 5

$ABC$ is a right-angled triangle.

 

Question 5(a) [2 marks]

Calculate the size of angle $CAB$

Give your answer correct to $3$ significant figures.

 

Answer type: Simple text answer

ANSWER: 38.7 $\degree$

WORKING:

Using SOHCAHTOA,

$\tan \theta = \dfrac{\text{O}}{\text{A}} = \dfrac{8}{10}$

$\theta = \tan^{-1} \bigg( \dfrac{8}{10} \bigg) = 38.7 \degree$ ($3$ sf)

 

 

 

Question 5(b) [1 mark]

The length of side $BC$ is reduced by $1$ cm

The length of the side $AB$ is still $10$ cm.

Angle $ABC$ is still $90 \degree$

 

What will happen to the value of $\tan CAB$?

 

Answer type: Multiple choice type 1

A: Increase

B: Decrease

C: Stay the same

 

ANSWER: B

WORKING:

Decrease: $\,\,\, \dfrac{7}{10} < \dfrac{8}{10}$

 

 

---

 

Question 6

There are some sweets in a bag.

The sweets are red, green, yellow or blue.

Tom is going to take at random a sweet from the bag.

The table below shows each of the probabilities that the sweet will be green or will be blue.

There are $5$ green sweets in the bag.

The probability that the sweet Tom takes will be blue is three times the probability that the sweet will be yellow.

 

Question 6(a) [4 marks]

Calculate the number of blue sweets in the bag.

 

Answer type: Simple text answer

ANSWER: 6

WORKING:

There are $5 \div 0.25 = 20$ sweets in total in the bag.

 

Let $x$ be the probability of selecting a yellow sweet,

$0.35 + 0.25 + x +3x = 1$

$0.6 + 4x = 1$

$4x = 0.4$

$x = 0.1$

 

So the probability of selecting a yellow sweet is $0.1$, and the probability of selecting a blue sweet is $0.3$

 

Hence, there are $20 \times 0.3 = 6$ blue sweets in the bag

 

 

 

 

Question 6(b) [1 mark]

A counter is going to be taken at random from a box.

The probability that the counter will be black is $0.25$

 

Janie says that there must be an even number of counters in the box.

Graham says that there must be an odd number of counters in the box.

Susan says that there can be either an odd number of counters or an even number of counters in the box.

 

Who is correct?

 

Answer type: Multiple choice type 1

A: Janie

B: Graham

C: Susan

 

ANSWER: A

WORKING:

$0.25$ multiplied by an odd number will not give a whole number, so there must be an even number of counters in the box.

Therefore Janie is correct.

 

---

 

Question 7 [3 marks]

Solve $\,\,\,\,\, \dfrac{3-2x}{3} = x-1$

Give your answer as a decimal.

 

Answer type: Simple text answer

ANSWER: 1.2

WORKING:

$\dfrac{3-2x}{3} = x-1$

$3-2x = 3(x-1)$

$3-2x = 3x - 3$

$3 = 5x - 3$

$6 = 5x$

$x = \dfrac{6}{5} = 1.2$

 

---

 

Question 8 [5 marks]

$ABCDEF$ is a hexagon.

 

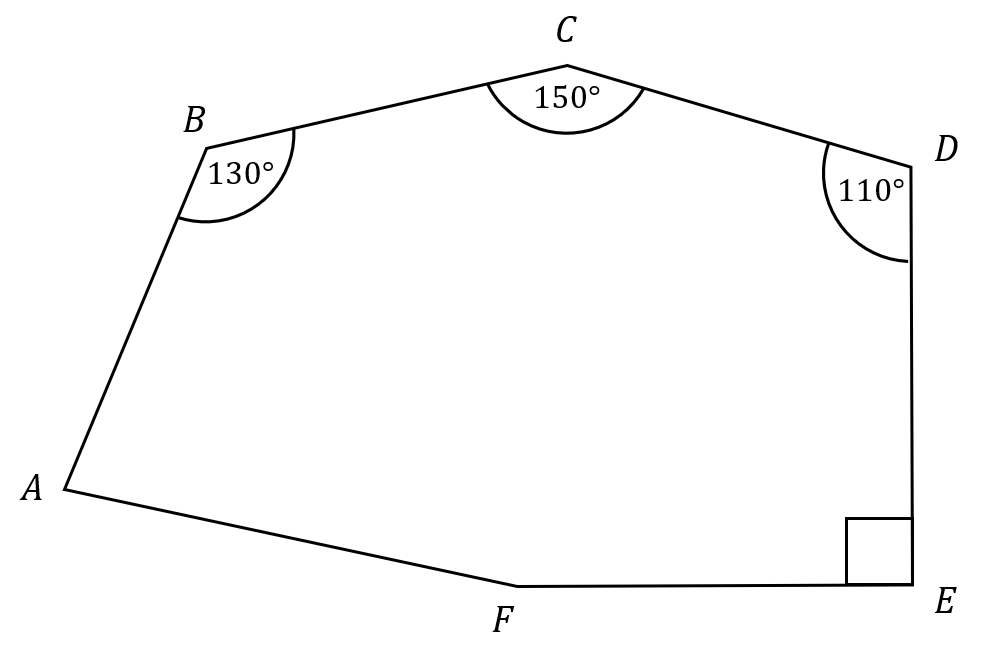
Angle $AFE = 2 \, \times$ Angle $BAF$

 

Calculate the size of angle $AFE$

 

Answer type: Simple text answer

ANSWER: 160 $\degree$

WORKING:

Let angle $BAF = x$, then angle $AFE = 2x$

 

Sum of interior angles $= 180 \times (n-2) = 180 \times (6-2) = 190 \times 4 = 720 \degree$

 

$90 + 110 + 150 + 130 + x + 2x = 720$

$480 + 3x = 720$

$3x = 240$

$x = 80 \degree$

 

So, angle $AFE = 2x = 2 \times 80 = 160 \degree$

 

---

 

Question 9

$Q = 2 \, \sqrt{\dfrac{a}{b^2}}$

 

$a = 3.2 \times 10^{-3}$

$b = 9.5 \times 10^{-4}$

 

Question 9(a) [2 marks]

Calculate the value of $Q$ in standard form to $3$ significant figures.

 

Answer type: Multiple choice type 1

A: $1.19 \times 10^2$

B: $1.19 \times 10^3$

C: $3.76$

D: $3.76 \times 10^2$

 

ANSWER: A

WORKING:

$Q = 2 \, \sqrt{\dfrac{3.2 \times 10^{-3}}{(9.5 \times 10^{-4})^2}} = 119.091... = 1.19 \times 10^2$ ($3$ sf)

 

 

 

Question 9(b) [2 marks]

$a$ decreased by $2 \%$

$b$ decreased by $5 \%$

 

What will happen to the value of $Q$ now?

 

Answer type: Multiple choice type 1

A: $Q$ will increase

B: $Q$ will decrease

C: $Q$ will stay the same

 

ANSWER: A

WORKING:

Scale factor $= \sqrt{\dfrac{0.98}{(0.95)^2}} = 1.042...$

 

The scale factor is greater than $1$, so the value of $Q$ will increase.

 

---

 

Question 10 [3 marks]

There are three stopwatches.

Stopwatch $A$ buzzes every $30$ seconds

Stopwatch $B$ buzzes every $60$ seconds

Stopwatch $C$ buzzes every $25$ seconds

The three stopwatches start buzzing at the same time.

 

How many times in on hour will the stopwatches buzz at the same time?

 

Answer type: Simple text answer

ANSWER: 12

WORKING:

A: $30 \,\, 60 \,\, 90 \,\, 120 \,\, 150 \,\, 180 \,\, 210 \,\, 240 \,\, 270 \,\, 300 \,\, 330 \,\, 360 \,\, ...$

B: $60 \,\, 120 \,\, 180 \,\, 240 \,\, 300 \,\, 360 \,\, ...$

C: $25 \,\, 50 \,\, 75 \,\, 100 \,\, 125 \,\, 150 \,\, 175 \,\, 200 \,\, 225 \,\, 250 \,\, 275 \,\, 300 \,\, 325 \,\, 350 \,\, 375 \,\, ...$

 

$300$ appears in all three

 

So,

$1$ time $= 300$ seconds $= 5$ minutes

$\dfrac{60}{5} = 12$ times in $60$ minutes

 

---

 

Question 11 [3 marks]

 

In $2010$, Chesney bought a motorbike.

 

In $2013$, Chesney sold the motorbike to Arnold.

Chesney made a profit of $15 \%$

 

In $2015$, Arnold sold the motorbike for $£8740$

He made loss of $5 \%$

 

Calculate how much Chesney paid for the motorbike in $2010$

 

Answer type: Simple text answer

ANSWER: £8000

WORKING:

Price in $2010 = x$

Price in $2013 = 1.15x$

Price in $2015 = 0.95(1.15x)$

 

$0.95(1.15x) = £8740$

$1.15x = £8740 \div 0.95 = £9200$

$x = £9200 \div 1.15 = £8000$

 

---

 

Question 12

The graph shows the volume of a gas in a container at time $t$ hours.

 

Question 12(a) [2 marks]

Find the gradient of the graph.

 

Answer type: Simple text answer

ANSWER: -2

WORKING:

Gradient $= \dfrac{\text{Change in } y}{\text{Change in } x} = \dfrac{16-2}{0 - 7} = - \dfrac{14}{7} = -2$

 

 

 

Question 12(b) [1 mark]

What does this gradient represent?

 

Answer type: Multiple choice type 1

A: The rate at which the container empties

B: The rate at which the container fills

 

ANSWER: A

 

 

Question  12(c) [1 mark]

What volume of gas is in the container at the start?

 

Answer type: Simple text answer

ANSWER: 16 m$^3$

WORKING:

$V = 16$ m$^3$ where the graph intersects the volume axis.

 

---

 

Question 13

Here are two similar solid shapes.

 

surface area of shape A : surface area of shape B $= 2:5$

The volume of shape $A$ is $25$ mm$^3$

Calculate the volume of shape $B$

Give you answer correct to $3$ significant figures.

 

Answer type: Simple text answer

ANSWER: 98.8 mm$^3$

WORKING:

shape A length : shape B length $= \sqrt{2} : \sqrt{5}$

 

Scale factor $= \dfrac{\sqrt{5}}{\sqrt{2}} = 1.581...$

(Scale factor)$^3$ $= (1.581...)^3 = 3.952...$

 

Volume of shape $B \, = 25 \times 3.952... = 98.8$ mm$^3$ ($3$ sf)

 

---

 

Question 14 [2 marks]

There are $18$ football teams in a league.

Each team played two matches against each of the other teams.

Calculate the total number of matches played.

 

Answer type: Simple text answer

ANSWER: 306

WORKING:

$18 \times 17 = 306$ matches in total.

 

---

 

Question 15

The following graph shows the speed of a motorbike, in metres per second, during the first $6$ seconds of a journey.

 

Question 15(a) [3 marks]

Estimate the distance the motorbike travelled in the first $6$ seconds.

Use $3$ strips of equal width.

 

Answer type: Multiple choice type 1

A: $49.4$ m

B: $52.6$ m

C: $45.8$ m

D: $56.2$ m

 

ANSWER: A

WORKING:

Split the graph into one triangle and two trapeziums, as follows:

 

$A = \dfrac{1}{2} \times 2 \times 8.8 = 8.8$ m

$B = \dfrac{1}{2} \times (8.8 + 10.4) \times 2 = 19.2$ m

$C = \dfrac{1}{2} \times (10.4 + 11) = 21.4$ m

 

Total distance travelled $\approx 8.8 + 19.2 + 21.4 = 49.4$ m

 

 

 

Question 15(b) [1 mark]

Is your answer to part (a) an underestimate or overestimate of the actual distance the motorbike travelled in the first $6$ seconds.

 

Answer type: Multiple choice type 1

A: Underestimate

B: Overestimate

 

ANSWER: A

WORKING:

There is some parts not included under the graph when we calculated the area of the shapes $A,B$ and $C$

So, the answer to part (a) is an underestimate.

 

---

 

Question 16

The $n$th term of a sequence is given by $an^2 + bn$, where $a$ and $b$ are integers.

The $1$st term is $-1$

The $3$rd term is $15$

 

 

Question 16(a) [4 marks]

Find the $5$th term of the sequence.

 

Answer type: Simple text answer

ANSWER: 55

WORKING:

$1$st term $(n=1)$: $\,\,\, a(1)^2 + b(1) = a + b = -1$

$3$rd term $(n = 3)$: $\,\,\, a(3)^2 + b(3) = 9a + 3b = 15$

 

Now we can solve the simultaneous equations,

$a+b = -1\,\,$ (1)

$9a+3b=15$ (2)

 

Multiply (1) by $3$: $\,\,\, 3a+3b=-3$

 

Subtract this new (1) from equation (2):

$6a = 18$

$a = 3$

 

Substitute $a=3$ into the original equation (1):

$3+b=-1$

$b = -4$

 

So, the $n$th term of the sequence is:

$3n^2 - 4n$

 

$5$th term $= 3(5)^2 - 4(5) = 75 - 20 = 55$

 

 

 

 

Question 16(b) [2 marks]

Here are the first $5$ terms of a different quadratic sequence.

$0 \,\,\,\,\, 3 \,\,\,\,\, 8 \,\,\,\,\, 15 \,\,\,\,\, 24$

 

Choose the correct expression representing the $n$th term of this sequence.

 

Answer type: Multiple choice type 1

A: $n^2 - 1$

B: $n^2 - n$

C: $2n^2 - 2$

D: $1 - n^2$

 

ANSWER: A

WORKING:

Quadratic sequence in the form $an^2 + bn + c$

 

Sequence: $\,\,\,0 \,\,\,\,\, 3 \,\,\,\,\, 8 \,\,\,\,\, 15 \,\,\,\,\, 24$

Differences: $\,\,\,3 \,\,\,\,\, 5 \,\,\,\,\, 7 \,\,\,\,\, 9$

$2$nd differences: $\,\,\,2 \,\,\,\,\, 2\,\,\,\,\, 2 \,\,\,\,\,2$

 

The $2$nd differences are $2$, so we half this to get $a = 1$

So, $n^2$ is the first part of the sequence.

 

Sequence: $\,\,\,0 \,\,\,\,\, 3 \,\,\,\,\, 8 \,\,\,\,\, 15 \,\,\,\,\, 24$

$n^2$: $\,\,\,1  \,\,\,\,\, 4 \,\,\,\,\, 9\,\,\,\,\, 16 \,\,\,\,\, 25$

Difference: $\,\,\,-1 \,\,\,\,\, -1\,\,\,\,\, -1 \,\,\,\,\,-1$

 

So, $b = 0$ and $c = -1$

Hence, the $n$th term is $n^2 - 1$

 

---

 

Question 17 [5 marks]

 

Calculate the length of $CD$.

Give your answer correct to $1$ decimal place.

 

Answer type: Simple text answer

ANSWER: $11.9$ cm

WORKING:

Use sine rule to find $BD$:

Let $BD = x$

$\dfrac{x}{\sin38} = \dfrac{16.3}{\sin 114}$

$x = \dfrac{16.3 \sin38}{\sin 114} = 10.984...$ cm

 

Use cosine rule to find $CD$:

Let $CD = a$

$a^2 = 15.7^2 + (10.984...)^2 - 2(15.7)(10.984...) \cos 49$

$a^2 = 140.866...$

$a = 11.898... = 11.9$ cm ($1$ dp)

($a$ cannot be the negative value of the square root since it is a physical length)

---

 

Question 18

 

Question 18(a) [2 marks]

The equation $x^3 - x = 10$ has a solution between which two numbers?

 

Answer type: Multiple choice type 1

A: $2$ and $3$

B: $1$ and $2$

C: $3$ and $4$

D: $0$ and $1$

 

ANSWER: A

WORKING:

$2^3 - 2 = 8 - 2 = 6$

$3^3 - 3 = 27 - 3 = 24$

 

$6 < 10 < 24$ so there is a solution is between $2$ and $3$

 

 

 

Question 18(b) [1 mark]

Choose the correct rearrangement of the equation $x^3 - x = 10$

 

Multiple choice type 1

A: $x = \sqrt[3]{x+10}$

B: $x = \sqrt[3]{10 - x}$

C: $x = \sqrt{x+10}$

D: $x = \sqrt[3]{x-10}$

 

ANSWER: A

WORKING:

$x^3 - x = 10$

$x^3 = x+10$

$x = \sqrt[3]{x+10}$

 

 

 

Question 18(c) [3 marks]

Starting with $x_0 = 2$,

use the iteration formula $x_{n+1} = \sqrt[3]{x+10}$ four times to find an estimate for a solution of $x^3 - x = 10$

Give your answer to $3$ decimal places.

 

Answer type: Simple text answer

ANSWER: 2.309

WORKING:

$\sqrt[3]{2+10} = 2.2894...$

$\sqrt[3]{2.2894...+10} = 2.3076...$

$\sqrt[3]{2.3076...+10} = 2.3088...$

$\sqrt[3]{2.3088...+10} = 2.3089...$

 

---

 

Question 19 [5 marks]

Below are two right-angled triangles.

 

Given that

$\cos p = \cos q$

find the value of $x$.

 

Answer type: Simple text answer

ANSWER: x = 4

WORKING:

$\cos \theta = \dfrac{\text{A}}{\text{H}}$

 

$\cos p = \dfrac{x}{3x-1}$

$\cos q = \dfrac{5x+8}{13x+25}$

 

$\cos p = \cos q$, then

$\dfrac{x}{3x-1} = \dfrac{5x+8}{13x+25}$

We now solve this for $x$

 

$x = \dfrac{(3x-1)(5x+8)}{13x+25}$

$x(13x+25) = (3x-1)(5x+8)$

$13x^2 + 25x = 15x^2 + 24x - 5x - 8$

$13x^2 + 25x = 15x^2 + 19x - 8$

$0 = 2x^2 - 6x - 8$

$0 = (2x+2)(x-4)$

$x = -1$ or $x = 4$

$x$ is a real physical length, so $x = 4$

 

---

 

Question 20

$40$ people were asked if they study History or Geography or Religious Education (RE).

 

Of these people,

$22$ study History

$3$ study History, Geography and RE

$4$ study History and RE, but not Geography

$7$ study Geography and RE

$5$ do not study any of the subjects

$8$ of the $9$ people who study Geography study at least one of the other subjects

 

Two of the people are chosen at random.

Calculate the probability that they both only study RE.

Give your answer as a fraction in simplest form.

 

Answer type: Fraction

ANSWER: $\dfrac{7}{195}$

WORKING:

Create a Venn diagram by using the information given, and calculating the remaining parts

There are $8$ out of $40$ people studying only RE.

If that one person is taken out, then there are $7$ people out of $39$ studying only RE.

Probability $= \dfrac{8}{40} \times \dfrac{7}{39} = \dfrac{56}{1560} = \dfrac{7}{195}$

 

---

 

Question 21 (Marks swapped compared to edexcel paper – was 3 for (a) then 2 for (b) – now 2 for (a) then 3 for (b))

 

$ABCD$ is a parallelogram.

$EAB$ and $DC$ are straight lines.

$\angle EFD = 90 \degree$

 

Question 21(a) [2 marks]

Choose the correct statement regarding triangle $AFE$ and triangle $DFC$

 

Answer type: Multiple choice type 1

A: They are similar, but may not be congruent

B: They are congruent

C: They are neither congruent nor similar

 

ANSWER: A

WORKING:

$AD$ and $BC$ are parallel, since $ABCD$ is a parallelogram.

$\angle AFE = \angle DFC$ (vertically opposite angles)

$\angle EAF = \angle CDF$ (alternate angles)

 

The two triangles have at two angles the same, so they mush be similar.

We don’t have any information about the lengths of the sides of the triangles, so they may not be congruent.

 

 

 

Question 21(b) [3 marks]

Given that $\angle EAF = 50 \degree$

find the value of $x \degree$

 

Answer type: Simple text answer

ANSWER: x = 40 $\degree$

WORKING:

$\angle AFE = 90 \degree$ (angles on a straight line)

$\angle AEF = 180 - 90 - 50 = 40 \degree$ (angles in a triangle)

$\angle FCD = 40 \degree$ (alternate angles)

$x = 40 \degree$ (vertically opposite angles)