NOTE: Q19-26 are the same as Q1-8 on June 18 Higher Paper 3
(DOESN’T NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Q4 – Only 2 parts, 1 mark then 2 marks, rather than 3 1 mark questions like in edexcel.
Question 1 [1 mark]
Write \dfrac{2}{10} as a decimal.
Answer type: Simple text answer
ANSWER: 0.2
Question 2 [1 mark]
Write 0.55 as a percentage.
Answer type: Simple text answer
ANSWER: 55 \%
Question 3 [1 mark]
Write 7856 correct to the nearest hundred.
Answer type: Simple text answer
ANSWER: 7900
Question 4
Here are the first 4 terms of a sequence.
3 \,\,\,\,\,\,\,\,\,\, 11 \,\,\,\,\,\,\,\,\,\,19 \,\,\,\,\,\,\,\,\,\,27
Question 4(a) [1 mark]
What is the next term in the sequence?
Answer type: Simple text answer
ANSWER: 35
WORKING:
Add 8 onto the last term: \,\,\,27+8 = 35
Question 4(b) [2 marks]
What is the 50th term in the sequence?
Answer type: Simple text answer
ANSWER: 395
WORKING:
nth term = 8n - 5
50th term = 8(50) - 5 = 395
Question 5
Here are four digits.
6 \,\,\,\,\,\,\,\,\,\, 5 \,\,\,\,\,\,\,\,\,\, 2 \,\,\,\,\,\,\,\,\,\, 8
Question 5(a) [1 mark]
Use all four digits to write down the smallest possible 4-digit number.
Answer type: Simple text answer
ANSWER: 2568
Question 5(b) [1 mark]
Write down the answer to the largest possible sum using all four digits.
Answer type: Simple text answer
ANSWER: 867
WORKING:
865 + 2 = 867
Question 6 [2 marks]
What are all of the factors of 20?
Answer type: Multiple choice type 1
A: 1, 2, 4, 5, 10, 20
B: 2, 4, 5, 10
C: 1, 2, 4, 5, 10
D: 2, 4, 5, 10, 20
ANSWER: A
Question 7 [2 marks]
Freddy has twice as many siblings as Helen.
Helen has three times as many siblings as Amir.
Amir has 1 sibling.
How many siblings does Freddy have?
Answer type: Simple text answer
ANSWER: 6
WORKING:
Helen has 3\times1=3 siblings.
Freddy then has 2\times3=6 siblings.
Question 8
Question 8(a) [1 mark]
Calculate \,\,\,\sqrt{2.56 \times 1.21}
Answer type: Simple text answer
ANSWER: 1.76
Question 8(b) [2 marks]
Calculate \,\,\,(2.82 - 0.48)^2 + 1.032
Answer type: Simple text answer
ANSWER: 6.5076
Question 9
This is part of a bus timetable between Leeds and Wakefield.

Question 9(a) [1 mark]
How many minutes should the 10 \, 30 bus take to go from Leeds to Wakefield?
Answer type: Simple text answer
ANSWER: 46 minutes
WORKING:
The time between 10 \, 30 and 11 \, 16 is 46 minutes
Question 9(b) [3 marks]
Gareth goes from Hunslet to Wakefield by Bus.
Gareth takes 18 minutes to get from his house to the bus stop in Hunslet.
He takes 10 minutes to get from the bus stop in Wakefield to work.
Gareth has to get to work by 9.45 am
He leaves his house at 8.30 am
Will Gareth get to work by 9.45 am?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: A
WORKING:
8.30 am + \, 18 minutes = 8.48 am at bus stop
He can therefore catch the 8.53 am bus from Hunslet
He arrives in Wakefield at 9.32 am
9.32 am + \, 10 minutes = 9.42 am when he arrives at work.
Therefore he gets to work on time.
Question 10 [3 marks]
Damien works as a labourer.
The table below gives his rates of pay.

Damien worked a total of 40 hours last week.
He worked 16 of these hours at the weekend.
His colleague, Fred, got paid £400 last week.
How much more did Fred get paid than Damien?
Answer type: Simple text answer
ANSWER: £20.80
WORKING:
40-16 = 24 hours worked during week
24 \times £8.80 = £211.20
16 hours worked at the weekend
16 \times £10.50 = £168.00
Total = £211.20 + £168.00 = £379.20
Difference = £400.00 - £379.20 = £20.80
Question 11 [2 marks]
Last year the cost of an annual golf club membership was £850
This year the cost of an annual golf club membership has been increased to £900
Write down the increase in the cost of an annual golf club membership as a fraction of last year’s cost.
Give your answer in its simplest form.
Answer type: Fraction
ANSWER: \dfrac{1}{17}
WORKING:
Increase = 900 - 850 = 50
\dfrac{50}{850} = \dfrac{1}{17}
Question 12 [5 marks]
The diagram shows a scale drawing of a field.

The scale of the drawing is 1:2500
Luna runs around the perimeter of the field 3 times.
Calculate the distance she runs in total.
Give your answer in kilometres.
Answer type: Simple text answer
ANSWER: 3.345 km
WORKING:
Perimeter of drawing = 13.2 + 13.2 + 9.1 + 9.1 = 44.6 cm
Perimeter of field in cm = 44.6 \times 2500 = 111500 cm
Perimeter of field in m = 111500 \div 100 = 1115 m
Perimeter of field in km = 1115 \div 1000 = 1.115 km
Distance ran = 3 \times 1.115 = 3.345 km
Question 13 [2 marks]
Below are two straight line graphs.

Match each equation in the table below to the correct graph.
One has been done for you.
Write the number of the graph to the match the corresponding letter from the table.

Answer type: Multiple answers type 1
ANSWERS:
a = 3
b = 6
c = 5
WORKING:
For y=5-x we can see that when x=0, y=5. And when y=0, x=5, so the graph is a straight line that goes through these two points.
x+y=0 can be rearranged into a more familiar form: \,\, y = -x
Question 14
Below are the ages of 15 people in a restaurant.
68 \,\,\,\,\, 38 \,\,\,\,\, 34 \,\,\,\,\, 64 \,\,\,\,\, 38 \,\,\,\,\, 43 \,\,\,\,\, 46 \,\,\,\,\, 52
31 \,\,\,\,\, 65 \,\,\,\,\, 50 \,\,\,\,\, 39 \,\,\,\,\, 66 \,\,\,\,\,46\,\,\,\,\,61
Question 14(a) [3 marks]
Choose the correctly completed stem and leaf diagram and key.
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: B
WORKING:
Order the numbers from smallest to largest:
31 \,\,\,\,\, 34 \,\,\,\,\, 38 \,\,\,\,\, 38 \,\,\,\,\, 39 \,\,\,\,\, 43 \,\,\,\,\, 46 \,\,\,\,\, 46
50 \,\,\,\,\, 52 \,\,\,\,\, 61 \,\,\,\,\, 64 \,\,\,\,\, 65 \,\,\,\,\,66\,\,\,\,\,68
Our key, for example is 6|5 = 65, where 6 is the stem and 5 is the leaf.
We then write the stem values into the diagram on the left, which are 3,4,5 and 6, and then fill in the leaves as the last digits of each number.
We write our leaves in order from smallest to largest.
Question 14(b) [2 marks]
One of these people in the restaurant is going to be chosen at random to win a free dessert.
What is the probability that this person is aged under 45?
Give your answer as a percentage.
Answer type: Simple text answer
ANSWER: 40 \%
WORKING:
There are 6 people aged under 45 out of a possible 15
Probability = \dfrac{6}{15} \times 100 = 40 \%
Question 15
Question 15(a) [1 mark]
Calculate \,\,\,16 - 6 \times 2
Answer type: Simple text answer
ANSWER: 4
WORKING:
Using BIDMAS, we need to calculate the multiplication first, then the subtraction
16 - 6 \times 2 = 16 - 12 = 4
Question 15(b) [1 mark]
Benny is asked to find the median of the numbers \,\,\,\,\, 4 \,\,\,\,\, 2 \,\,\,\,\, 9 \,\,\,\,\, 6 \,\,\,\,\, 2
How should he find the median?
Choose the correct statement.
Answer type: Multiple choice type 1
A: He needs to order the numbers in numerical order before finding the middle number, so the median is 4
B: He needs to add the first and last number together and divide by 2, so the median is 3
C: He needs to find the most common number, so the median is 2
D: He needs to find the middle number, so the median is 9
ANSWER: A
WORKING:
The median is the middle value of an numerically ordered list of numbers
Order the numbers from smallest to largest: \,\,\, 2 \,\,\,\,\, 2 \,\,\,\,\, 4 \,\,\,\,\, 6 \,\,\,\,\, 9
Then the median is the middle number, which is 4
Question 16
Geoff, Bupsi and Lian share a some money.
Geoff gets \dfrac{1}{6} of the money
Bupsi gets \dfrac{1}{3} of the money
Lian gets the rest of the money.
Geoff gets \$7.50
Question 16(a) [2 marks]
Calculate how much money Bupsi gets.
Answer type: Simple text answer
ANSWER: \$ 15
WORKING:
Geoff = \$ 7.50 = \dfrac{1}{6}
Total = \$7.50 \times 6 = \$45
Bupsi = \$ 45 \times \dfrac{1}{3} = \$15
Question 16(b) [3 marks]
Find the ratio
Amount of money Geoff gets : Amount of money Lian gets
Give your answer in its simplest form a:b where a and b are whole numbers.
Answer type: Multiple answers type 1
ANSWERS:
a = 1
b = 3
WORKING:
Lian gets 1 - \dfrac{1}{3} - \dfrac{1}{6} = \dfrac{1}{2} of the money
Lian = \$45 \times \dfrac{1}{2} = \$22.50
Geoff : Lian = 7.50 : 22.50 = 1 : 3
Question 17 [3 marks]
ABCD is a rectangle.

The area of the rectangle is 588 mm^2
Find x
Answer type: Simple text answer
ANSWER: x = 7
WORKING:
Area = 4x \times 3x = 12x^2
12x^2 =588
x^2 = 49
x = 7
(x must be positive since it represents a physical length)
Question 18 [2 marks]
Calculate \,\,\, \dfrac{7.755 \times 10^8}{2.35 \times 10^4}
Give your answer in standard form.
Answer type: Multiple choice type 1
A: 3.3 \times 10^4
B: 3.3 \times 10^{12}
C: 18.22425 \times 10^4
D: 3.3 \times 10^2
ANSWER: A
WORKING:
\dfrac{7.755 \times 10^8}{2.35 \times 10^4}
= \dfrac{7.755}{2.35} \times \dfrac{10^8}{10^4}
= 3.3 \times 10^{8-4}
= 3.3 \times 10^4
Question 19
The scatter diagram shows information about 10 boys.
It shows the age of each boy and the best distance he jumps in a long jump competition.

Question 19(a) [1 mark]
What type of correlation does the scatter graph show?
Answer type: Multiple choice type 1
A: Positive correlation
B: Negative correlation
C: No correlation
ANSWER: A
Question 19(b) [1 mark]
Adam is 15 years old.
His best long jump is 6.1 m
Which statement correctly describes the point representing this information?
Answer type: Multiple choice type 1
A: The point is an outlier
B: The point is in line with the trend of the other points
ANSWER: A
Question 19(c) [1 mark]
Mark is 19 years old.
mark says
“The scatter diagram shows that I should jump at least 6.5 m on a long jump”
Choose the correct statement regarding his comment.
Answer type: Multiple choice type 1
A: The point would be outside the range of the scatter diagram
B: the point would be inside the range of the scatter diagram
ANSWER: A
Question 20 [2 marks]
Expand and simplify 4(r+2) - 3(1-3r)
Answer type: Multiple choice type 1
A: 13r + 5
B: 5 - 5r
C: 13r - 5
D: 5r - 5
ANSWER: A
WORKING:
4(r+2) - 3(1-3r)
= 4r + 8 - 3 + 9r
= 13r + 5
Question 21 [2 marks]
Here is a triangle drawn on a centimetre grid.

Calculate the length of one side of a square that is equal in area to the triangle above.
Answer type: Simple text answer
ANSWER: 3 cm
WORKING:
Area of triangle = \dfrac{1}{2} \times 6 \times 3 = 9 cm^2
Area of square = 9 cm^2
Side length of square = \sqrt{9} = 3 cm
Question 22
When a biased 4 sided spinner is spun once, the probability that it will land on 1 is 0.40
The biased spinner is spun twice.
Abdul starts drawing the probability tree diagram.
Choose the correctly completed probability tree diagram based on this information.
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: A
WORKING:
Probability of landing on 1 = 0.4
Probability of NOT landing on 1 = 1 - 0.4 = 0.6
Question 23
ABC is a right-angled triangle.

Question 23(a) [2 marks]
Calculate the size of angle CAB
Give your answer correct to 3 significant figures.
Answer type: Simple text answer
ANSWER: 38.7 \degree
WORKING:
Using SOHCAHTOA,
\tan \theta = \dfrac{\text{O}}{\text{A}} = \dfrac{8}{10}
\theta = \tan^{-1} \bigg( \dfrac{8}{10} \bigg) = 38.7 \degree (3 sf)
Question 23(b) [1 mark]
The length of side BC is reduced by 1 cm
The length of the side AB is still 10 cm.
Angle ABC is still 90 \degree
What will happen to the value of \tan CAB?
Answer type: Multiple choice type 1
A: Increase
B: Decrease
C: Stay the same
ANSWER: B
WORKING:
Decrease: \,\,\, \dfrac{7}{10} < \dfrac{8}{10}
Question 24
There are some sweets in a bag.
The sweets are red, green, yellow or blue.
Tom is going to take at random a sweet from the bag.
The table below shows each of the probabilities that the sweet will be green or will be blue.

There are 5 green sweets in the bag.
The probability that the sweet Tom takes will be blue is three times the probability that the sweet will be yellow.
Question 24(a) [4 marks]
Calculate the number of blue sweets in the bag.
Answer type: Simple text answer
ANSWER: 6
WORKING:
There are 5 \div 0.25 = 20 sweets in total in the bag.
Let x be the probability of selecting a yellow sweet,
0.35 + 0.25 + x +3x = 1
0.6 + 4x = 1
4x = 0.4
x = 0.1
So the probability of selecting a yellow sweet is 0.1, and the probability of selecting a blue sweet is 0.3
Hence, there are 20 \times 0.3 = 6 blue sweets in the bag
Question 24(b) [1 mark]
A counter is going to be taken at random from a box.
The probability that the counter will be black is 0.25
Janie says that there must be an even number of counters in the box.
Graham says that there must be an odd number of counters in the box.
Susan says that there can be either an odd number of counters or an even number of counters in the box.
Who is correct?
Answer type: Multiple choice type 1
A: Janie
B: Graham
C: Susan
ANSWER: A
WORKING:
0.25 multiplied by an odd number will not give a whole number, so there must be an even number of counters in the box.
Therefore Janie is correct.
Question 25 [3 marks]
Solve \,\,\,\,\, \dfrac{3-2x}{3} = x-1
Give your answer as a decimal.
Answer type: Simple text answer
ANSWER: 1.2
WORKING:
\dfrac{3-2x}{3} = x-1
3-2x = 3(x-1)
3-2x = 3x - 3
3 = 5x - 3
6 = 5x
x = \dfrac{6}{5} = 1.2
Question 26 [5 marks]
ABCDEF is a hexagon.
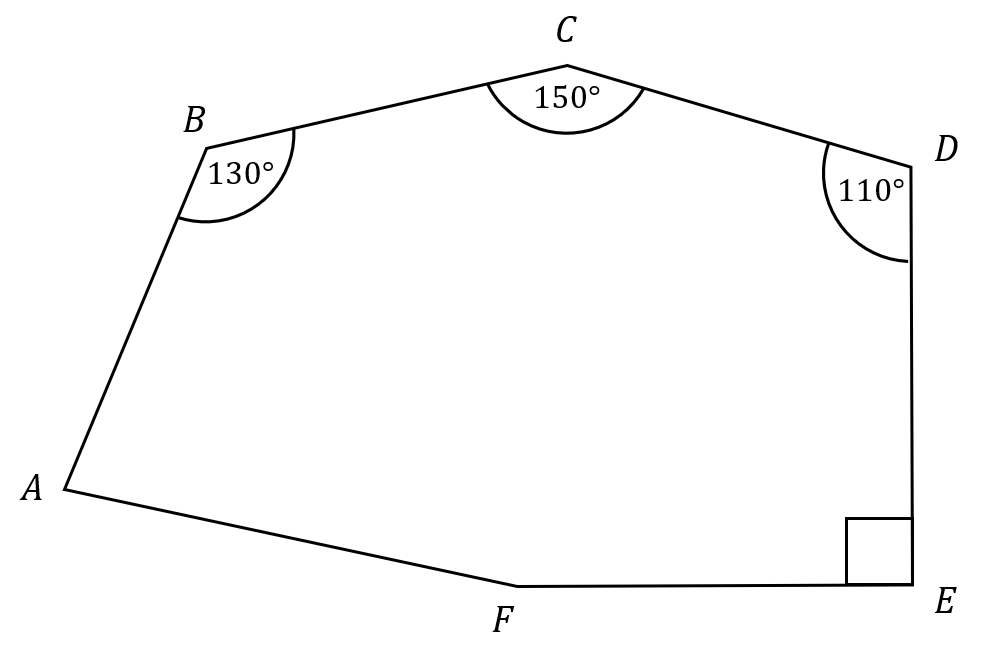
Angle AFE = 2 \, \times Angle BAF
Calculate the size of angle AFE
Answer type: Simple text answer
ANSWER: 160 \degree
WORKING:
Let angle BAF = x, then angle AFE = 2x
Sum of interior angles = 180 \times (n-2) = 180 \times (6-2) = 190 \times 4 = 720 \degree
90 + 110 + 150 + 130 + x + 2x = 720
480 + 3x = 720
3x = 240
x = 80 \degree
So, angle AFE = 2x = 2 \times 80 = 160 \degree
Question 27
Triangle ABC and DEF are mathematically similar.

Question 27(a) [2 marks]
Calculate the length of AB
Answer type: Simple text answer
ANSWER: 8.5 m
WORKING:
Scale factor = 13 \div 5.2 = 2.5
AB = 3.4 \times 2.5 = 8.5 m
Question 27(b) [2 marks]
Calculate the length of RQ
Answer type: Simple text answer
ANSWER: 3.2 m
WORKING:
8 \div 2.5 = 3.2 m
Question 28 [3 marks]
Make t the subject of the formula \,\,\, B = \sqrt{\dfrac{5 - t}{3}}
Answer type: Multiple choice type 1
A: t = 5 - 3B^2
B: t = 3B^2 - 5
C: t = 3B^2 + 5
D: t = 5 - 3B
ANSWER: A
WORKING:
B = \sqrt{\dfrac{5 - t}{3}}
B^2 = \dfrac{5-t}{3}
3B^2 = 5 - t
t + 3B^2 = 5
t = 5 - 3B^2
