1(a)
Work out 4\dfrac{1}{5}-2\dfrac{1}{3}
Give your answer as an improper fraction in its simplest form.
Answer type: fraction
Answer: 28 / 15
Workings:
4\dfrac{1}{5}-2\dfrac{1}{3}
=\dfrac{21}{5}-\dfrac{7}{3}
= \dfrac{63}{15}-\dfrac{35}{15}=\dfrac{28}{15}
2 marks
1(b)
Work out 2\dfrac{1}{4} \div \dfrac{3}{5}
Give your answer as a mixed number in its simplest form.
Annswer type: multiple choice
Answer: 3\dfrac{3}{4}
Wrong answers:
3\dfrac{1}{2}
2\dfrac{1}{5}
2\dfrac{3}{5}
Workings:
2\dfrac{1}{4} \div \dfrac{3}{5}
=\dfrac{9}{4}\div \dfrac{3}{5} = \dfrac{9}{4} \times \dfrac{5}{3} =\dfrac{45}{12}=3 \dfrac{9}{12} = 3 \dfrac{3}{4}2 marks
2
In an aquarium
the number of minnows and the number of clown fish are in the ratio 8:3
the number of clown fish and the number of gold fish are in the ratio 6:11
There are 33 gold fish in the aquarium
How many minnows are there in the aquarium?
Answer type: simple
Answer: 48
Workings:
The first ratio can be doubled so that the number of parts are the same for the clown fish in both ratios.
8:3 = 16:6Combining the two ratios gives the ratio of minnows : clown fish : gold fish as 16:6:11
There are 33 goldfish, which is 11 parts, thus
1 part =33 \div 3 = 11
There are 16 parts minnows, so the number of minnows = 16\times3 = 48
3 marks
Q3
Sally buys 10 kg of coffee to sell.
She pays £40 for the coffee in total.
Sally divides the coffee into smaller bags.
She puts 400g of coffee into each bag.
She sells each bag of coffee for £3
Sally sells all the bags of coffee.
Work out her percentage profit.
Give your answer to one decimal place.
Answer type: simple
Answer: 87.5
Workings:
The number of smaller bags of coffee is 10 kg \div \space 400 g
=10 kg \div\space 0.4 kg = 25 bags
She sells the bags at £3 each, so the total revenue is 25\times£3 = £75
The percentage profit can be calculated as follows:
Profit = \bigg(\dfrac{75-40}{40}\bigg)\times100 = \bigg(\dfrac{35}{40}\bigg)\times100=87.5 \%
4 marks
Q4
A train journey across Russia is 9608.5 kilometres in length.
The average speed of the train is 47.8 km per hour.
The train travels for 24 hours per day.
(a) Estimate how many days it will take to complete the train journey.
Answer type: simple
Answer: 8
Workings:
Rounding the figures in the question,
9608.5 km \approx 9600 km
47.8 km per hour \approx 50 km per hour
The distance covered each day can be estimated as
24\times50 = 1200 km
Thus, the time taken is 9600 \div 1200 = 8 days.
3 marks
The train is fitted with a new engine.
This increases its average speed.
It is now 55.4 km per hour.
(b) How does this affect your answer to part (a)?
Answer type: multiple choice
Answer: It will take less time to complete the journey
Wrong answers:
It will take more time to complete the journey
It will make no difference to the time taken to complete the journey
It is not possible to say
Workings:
A faster average speed will mean the journey takes less time to complete.
1 mark
Q5
The diagram below shows a solid square-based pyramid AWXYZ

The base of the pyramid is a square of side 8 cm.
The height of the pyramid is 4 cm.
M is the midpoint of XY and AM=7 cm.
(a) Which of the following diagrams is an accurate side elevation of the pyramid from the direction of the arrow?
Correct answer:

Wrong Answers:



Workings:
The correct diagram is an isosceles triange with a width of 8 cm and a height of 6 cm
2 marks
(b)
Work out the total surface area of the pyramid.
Answer type: simple
Answer: 176 cm^2
Workings:
The area of each triangular face can be calculated as follows:
Area of triangle = \dfrac{1}{2}\times base \times height = \dfrac{1}{2}\times8\times7=28 cm^2
There are 4 triangular faces, so their combined area is 4\times28=112 cm^2
The area of the square base is 8\times8=64 cm^2
The total area is therefore 64+112 = 176 cm^2
4 marks
Q6
A pattern is made from 8 identical triangles.
The triangles are joined at the vertices and the bottom edge of the pattern is parallel to the x axis.

Point P has the coordinates (4,5)
Point Q has the coordinates (28,17)
Point R is marked on the diagram.
Work out the coordinates of point R
Answer type: multiple choice
Answer: (13,11)
Wrong Answers:
(13,10) (12,11) (12,10)
Workings:
Work out the x and y values separately.
x coordinate:
The distance in x from P to Q is 4 triangles and the distance in x from P to R is 1.5 triangles.
Thus the distance in x from P to R is \dfrac{1.5}{4} = \dfrac{3}{8} of the distance in x from P to Q
The distance in x from P to Q= 28-4=24
The distance in x from P to R is therefore 24\times \dfrac{3}{8} = 9
The x coordinate of R is therefore 4+9=13
y coordinate:
The distance in y from P to R is half the distance in y from P to Q
The distance in y from P to Q is 17-5=12
Half this distance is \dfrac{12}{2}=6
The y coordinate of R is therefore 5+6=11
Therefore the coordinates of R are (13,11)
5 marks
Q7

Shape A is rotated 180\degree about the point (1,2) to give shape B
Shape B is then reflected in the line y=2 to give shape C
Which of the following single transformations will map shape A onto shape C.
Answer type: multiple choice
Answer: Translation by the vector \begin{pmatrix} -4 \\ 0 \end{pmatrix}
Wrong answers:
Reflection in the line x=0
Rotation 180\degree about the point (1,3)
Translation by the vector \begin{pmatrix} -2 \\ 2 \end{pmatrix}
Workings:
Shapes A, B, and C are shown on the axis below.

As can be seen on the above axes, shape C is 4 squares to the left of A, so the single transformation mapping A onto C is a translation by the vector \begin{pmatrix} -4 \\ 0\end{pmatrix}
2 marks
Q8
The perimeter of a right-angled triangle 90 cm
The lengths of its sides are in the ratio 5:12:13
Work out the area of the triangle.
Answer: 270 cm^2
Workings:
Total parts = 5+12+13=30
Therefore one part =90 \div 30 = 3
The lengths of the sides are therefore:
5\times3=15 12\times3=36 13\times3=39The longest side of the triangle, so the sides with lengths 15 cm and 13 cm are the base and the height
Thus, area = 0.5\times13\times15=270 cm^2
4 marks
Q9
9(a)
Write down the value of 121^{\frac{1}{2}}
Answer: 11
Workings:
121^{\frac{1}{2}}=\sqrt{121}=111 mark
9(b)
Write down the value of 37^0
Answer: 1
Workings:
Anything to the power 0 is 1
1 mark
9(c)
Write down the value of 64^{-\frac{2}{3}}
Answer: 1/16
Workings:
\begin{aligned}64^{-\frac{2}{3}} &=\frac{1}{64^{\frac{2}{3}}} \\[1.5em] &= \frac{1}{(\sqrt[3]{64})^2} \\[1.5em] &=\dfrac{1}{4^2} \\[1.5em] &= \dfrac{1}{16}\end{aligned}2 marks
Q10
The table gives some information about the lengths of some planks of wood.
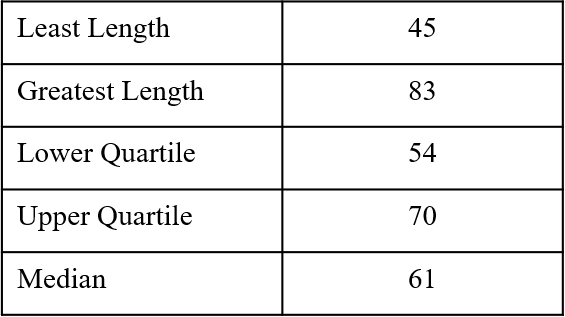
10(a)
Which of the following box plots correctly represents this information?
Answer:

Wrong Answers:


3 marks
10(b)
Work out an estimate for the number of planks of wood with a length between 54 cm and 83 cm
Answer: 30
Workings:
This range corresponds to everything except the lower quartile, so it is the remaining \dfrac{3}{4} of the data.
The number of planks in this range is therefore \dfrac{3}{4} \times 40 = 30
2 marks
11

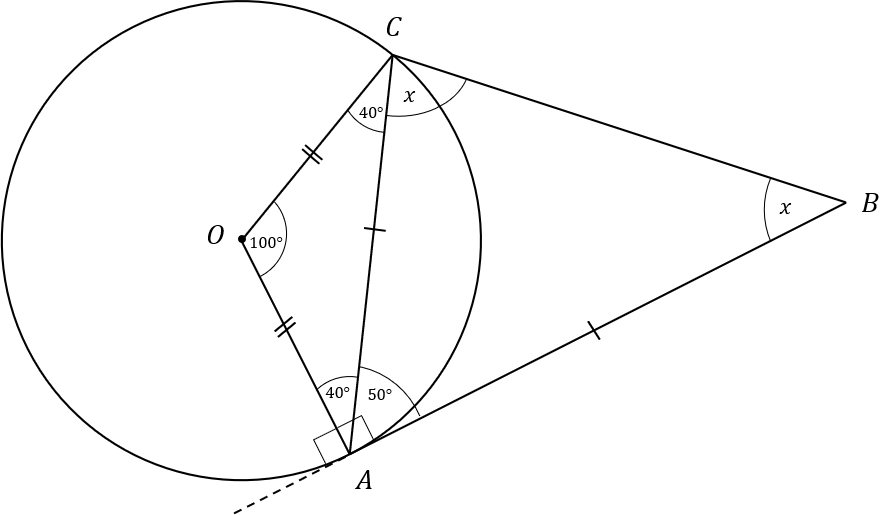
A and C are points on a circle, centre O.
AB is a tangent to the circle
Angle AOC = 100\degree
Find the size of angle x
Answer: x = 65 \degree
Workings:
There are two isosceles triangles, AOC and ABC
The ‘base’ angle in triangle AOC=\dfrac{180-100}{2}=\dfrac{80}{2}=40\degree
AB is a tangent to the circle, and OA is a radius, so angle OAB is a right angle.
Therefore angle CAB=90-40=50\degree
The remaining angles are both equal to x, so x=\dfrac{180-50}{2}=\dfrac{130}{2}=65\degree
5 marks
Q12
Prove that the product of any two odd numbers is always 1 more than a multiple of two.
Select the correct proof.
Answer type: multiple choice
Answer: 
Wrong answers:



4 marks
Q13
\sqrt{10}(\sqrt{2}+\sqrt{18}) can be written in the form a\sqrt{5} where a is an integer.
Find the value of a.
Answer type: simple
Answer: 8
Workings:
\begin{aligned}\sqrt{10}(\sqrt{2}+\sqrt{18}) &= \sqrt{20}+\sqrt{180} \\ &= \sqrt{4\times5}+\sqrt{36\times5} \\ &= 2\sqrt{5}+6\sqrt{5} \\ &= 8\sqrt{5}\end{aligned}3 marks
Q14
a is inversely proportional to m^2
When m=4, a=4
m is directly proportional to b^2
When b=3, m=54
Select the correct formula for a in terms of b
Give your answer in its simplest form.
Answer type: multiple choice
Answer: a=\dfrac{16}{9b^4}
Wrong answers:
a=\dfrac{64}{3b^2}
a=\dfrac{54}{3b^2}
a=\dfrac{32}{(9b)^2}
Workings:
a\propto \dfrac{1}{m^2} so a=\dfrac{k}{m^2}
When m=4, a=4, so
4=\dfrac{k}{4^2}=\dfrac{k}{16}So k=64, therefore a=\dfrac{64}{m^2}
m \propto b^2 so m=lb^2
When b=3, m=54 so 54=l\times3^2=9l
So l = 6, therefore m=6b^2
The two expressions can be combined:
\begin{aligned}a &=\dfrac{64}{m^2}\\[1.5em] &= \dfrac{64}{(6b^2)^2} \\[1.5em] &=\dfrac{64}{36b^4}\\[1.5em] &= \dfrac{16}{9b^4}\end{aligned}5 marks
Q15
15(a)
Factorise x^2-y^2
Select the correct option.
Answer type: multiple choice
Answer: (x+y)(x-y)
Wrong answers:
(x+y)^2
(x-y)^2
x(x+y^2)
Workings:
x^2-9=(x+y)(x-y)
1 mark
15(b)
Hence, or otherwise, select the fully simplified form of (a^2+8)^2-(a^2-12)^2
Answer type: multiple choice
Answer: 40(a^2-2)
Wrong answers:
20(a^2-4)
-8(a^2-2)
-8(a^2+2)
Workings:
Let a^2+8 = x and a^2-12 = y
(a^2+8)^2-(a^2-12)^2 = x^2-y^2
From part (a), x^2-y^2 = (x+y)(x-y), so
\begin{aligned}(x+y)(x-y) &= \Big( (a^2+8)+(a^2-12)\Big) \Big( (a^2+8)-(a^2-12) \Big) \\ &= (2a^2-4)\times20 \\ &= 40a^2 - 80 \\ &=40(a^2-2) \end{aligned}
3 marks
Q16
There are only black, green and red pens in a pencil case.
The ratio of the number of black pens to the number of green pens is 12:5
Andy takes at random a pen from the pencil case.
The probability that then pen is red is 0.15
Work out the probability that Andy takes a green pen from the pencil case.
Give your answer to two decimal places.
Answer type: simple
Answer: 0.25
Workings:
Probability red =0.15
Probability black or green =1-0.15=0.85
Ratio black : green =12:5 so total parts = 17
One part =0.85\div 17 = 0.05
Probability black = 0.05 \times 12 = 0.60
Probability green = 0.05\times 5 = 0.25
3 marks
Q17
Simplify fully \dfrac{2m^2+10m+12}{2m^2+4m}
Answer type: multiple choice
Answer: \dfrac{m+3}{m}
Wrong answers:
\dfrac{2m+6}{2m}
\dfrac{m^2+5m+6}{2(m^2+m)}
\dfrac{2m+3}{2m}
Workings:
\begin{aligned}\dfrac{2m^2+10m+12}{2m^2+4m} &= \dfrac{2(m^2+5m+6)}{2(m^2+2m)} \\[1.5em] &= \dfrac{(m+3)(m+2)}{m(m+2)} \\[1.5em] &=\dfrac{m+3}{m}\end{aligned}3 marks
Q18
Here is a graph of y=\text{cos }x\degree for -180 \leq x \leq 180

Choose the correct sketch of y=-\text{cos }x\degree for -180 \leq x \leq 180
Answer type: multiple choice
Answer: 
Wrong answers:



Workings:
The graph of y = -\text{cos }x\degree corresponds to a reflection in the x axis
2 marks
Q19
The point A has the coordinates (4,13)
The point B has the coordinates (p,q)
A line perpendicular to AB is given by the equation 5y+2x=7
Find an expression for the line that goes through A and B in the form y=mx+c.
Hence give the values of m and c, rounding your answers to one decimal place where appropriate.
Answers:
m = 2.5
c = 3
Workings:
Rearranging the equation of the perpendicular line:
\begin{aligned}5y+2x &= 7 \\5y &=-2x+7 \\ y &= -\frac{2}{5}x+7 \end{aligned}The gradient of the line AB is -1 \div -\dfrac{2}{5} = \dfrac{5}{2}
So m=\dfrac{5}{2}=2.5
Substituting in the coordinates of A (4,13) to y=mx+c gives:
13=-\dfrac{5}{2}\times4 + c =10+c
So c=3
The expression is therefore y=\dfrac{5}{2}x+3 or y = 2.5x+3
5 marks
Q20
x is an integer such that 4x+13 < 33 and \dfrac{x^2}{x+6}<1
Select the possible values of x.
Answer type: multiple choice
Answer: x = -1, 0, 1, 2
Wrong answers:
x=-2-1,0,1,2,3
x=1,2,3,4,5
x=-2,-1,0,1
Workings:
\begin{aligned}4x+13 &< 33 \\ 4x &< 20 \\ x &< 5\end{aligned}
So x is less than 5
\begin{aligned} \dfrac{x^2}{x+6} &< 1 \\[1.2em] x^2 &< x+6 \\ x^2-x-6 &< 0 \\ (x+2)(x-3) &< 0\end{aligned}
x=-2, \quad x=3
-2<x<3
Hence the numbers that satisfy both inequalites are:
x = -1, 0, 1, 2
5 marks
