NOTE: Q1-7 are the same as Q20-26 on Nov 18 Foundation Paper 1
(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1 [2 marks]
Work out the value of \dfrac{2^5 \times 2^{-3}}{2^4}
Give your answer in its simplest form.
Answer type: Fraction
ANSWER: \dfrac{1}{4}
WORKING:
\dfrac{2^5 \times 2^{-3}}{2^4} = \dfrac{2^2}{2^4} = \dfrac{4}{16} = \dfrac{1}{4}Question 2
a^2 = 2b^2 - cd
b = 3 \,\,\,\,c = 2 \,\,\,\,d = 1
Question 2(a) [2 marks]
Work out the positive value of a
Answer type: Simple text answer
ANSWER: 4
WORKING:
a^2 = 2(3)^2 - (2)(1) = 18 - 2 = 16
a = \sqrt{16} = \pm 4
So the positive value of a = 4
Question 2(b) [2 marks]
Make c the subject of a^2 = 2b^2 - cd
Answer type: Multiple choice
A: c = \dfrac{2b^2 - a^2}{d}
B: c = \dfrac{a^2 - 2b^2}{d}
C: c = \dfrac{2b^2 - d}{a^2}
D: c = \dfrac{d}{2b^2 - a^2}
ANSWER: A
WORKING:
a^2 + cd = 2b^2
cd = 2b^2 - a^2
c = \dfrac{2b^2 - a^2}{d}
Question 3 [5 marks]
A company decides to share a bonus of £12000 between the 20 members of staff who work for the company.
Out of 20 employees there are 5 managers and 15 are sales personnel.
The company is deciding between two options.
Option 1:
40\% of the bonus is going to be shared equally between the 5 managers.
The rest of the bonus is shared equally between 15 sales personnel.
Option 2:
The bonus is shared equally between all 12 employees.
Work out the percentage increase in the value of the bonus each sales person receives if option 2 is selected rather than option 1?
Answer type: Simple text answer
ANSWER: 25 \%
WORKING:
Option 1:
12000 \times 0.6 = £7200 shared between sales team
£720 \div 15 = £480 each
Option 2:
If all 20 people shared the bonus equally, they would each get a £12000 \div 20 = £600 bonus
Percentage Increase:
\dfrac{600}{480} = \dfrac{60}{48} =\dfrac{6}{5} = 1.25
Percentage increase = 0.25 \times 100 = 25 \%
Question 4
It would take 150 minutes to fill a water tank using water from 6 taps.
Question 4(a) [2 marks]
How many minutes would it take to fill the tank if only 4 of the taps are used?
Answer type: Simple text answer
ANSWER: 225 minutes
WORKING:
150 minutes for 6 taps
150 \times 6 = 900 minutes for 1 tap
\dfrac{900}{4} = 225 minutes for 4 taps
Question 4(b) [1 mark]
Which of the following assumptions is correct based on your working out to part (a)?
Which one of the following statements is assumed in your answer to part(a)?
Answer type: Multiple choice
A: Each taps fills at the same rate
B: Each tap fills at a different rate
C: 4 taps will fill the pool quicker than 6 taps
D: 1 tap can fill the tank in 25 minutes
ANSWER: A
Question 5
A train travels at a speed of 98 miles per hour.
Question 5(a) [3 marks]
Estimate the number of seconds the train would take to travel 1 mile?
Answer type: Multiple choice
A: 36 seconds
B: 26 seconds
C: 18 seconds
D: 58 seconds
ANSWER: A
WORKING:
\text{Time in hours} = \dfrac{\text{distance}}{\text{speed}} = \dfrac{1}{98} \approx \dfrac{1}{100}
\text{Time in seconds} = \dfrac{1}{100} \times 60 \times 60 = 36 \, \, \text{seconds}
Question 5(b) [1 mark]
Is your answer to part (a) an underestimate or overestimate?
Answer type: Multiple choice
A: Underestimate
B: Overestimate
ANSWER: A
WORKING:
Underestimate as the speed is rounded up.
Question 6 [3 marks]
For the simultaneous equations
6x - 17y = 30
x - 4y = 12
Find the values of x and y
Answer type: Multiple answer
ANSWER:
x = -12
y = -6
WORKING:
6x - 17y = 30 \,\,\, (1)
6x - 24y = 72 \,\,\, (2)
Subtract (2) from (1) to get -7y = 42 so y = -6
Substitute y=-6 into (1) and solve
6x - 17(-6) = 30
6x + 102 = 30
6x = -72
x = -12
So, x = -12 and y = -6
Question 7 [4 marks]
The diagram shows a square \textit{ABCD} with sides of length 8 cm.
It also shows a semicircle and a quadrant.

\textit{BC} is the diameter of the semicircle.
\textit{AE} is the radius of the quadrant.
What is the area of the shaded region?
Answer type: Multiple choice
A: 64 - 9\pi cm^2
B: 8 - 9\pi cm^2
C: 64 + 9\pi cm^2
D: 8 + 9\pi cm^2
ANSWER: A
WORKING:
Area of the semicircle:
\dfrac{1}{2} \times \pi \times r^2 = \dfrac{1}{2} \times \pi \times 4^2 = \dfrac{1}{2} \times \pi \times 16 = 8 \pi cm^2
Area of the quadrant:
\dfrac{1}{4} \times \pi \times r^2 = \dfrac{1}{4} \times \pi \times 2^2 = \dfrac{1}{4} \times \pi \times 4 = \pi cm^2
Area of the square \textit{ABCD}\,:
8 \times 8 = 64 cm^2
Area of shaded region = 64 - 8\pi - \pi = 64 - 9\pi cm^2
Question 8(a) [1 mark]
What is the exact value of \cos \, 45^\circ?
Answer type: Multiple choice
A: \dfrac{1}{\sqrt{2}}
B: \sqrt{2}
C: 2
D: \dfrac{1}{2}
ANSWER: A
WORKING:
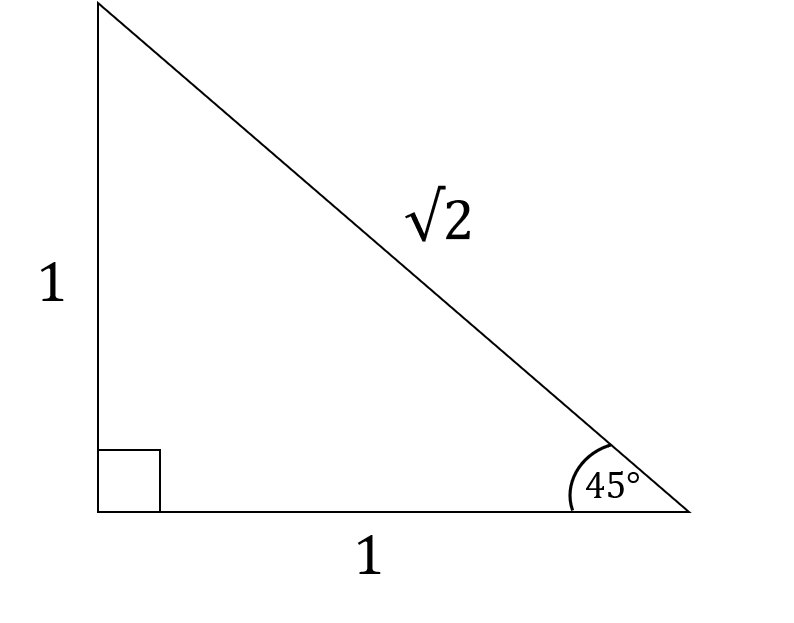
\text{cos} \, \theta = \dfrac{\text{adjacent}}{\text{hypotenuse}}
\text{cos} \, 45^\circ = \dfrac{1}{\sqrt{2}}
Question 8(b) [2 marks]
Here is a right-angled triangle.
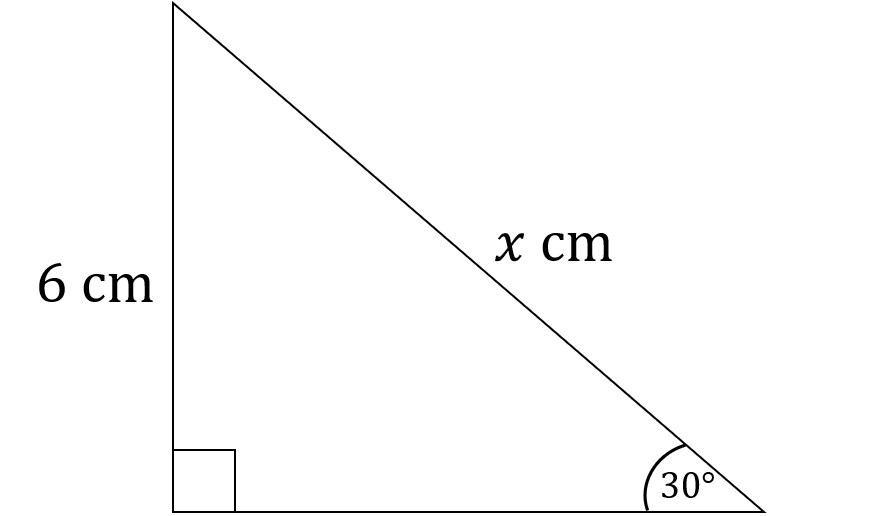
\text{sin} \, 30^\circ = \dfrac{1}{2}
What is the value of x?
Answer type: Simple text answer
ANSWER: 12 cm
WORKING:t
\text{sin} \, \theta = \dfrac{\text{opposite}}{\text{hypotenuse}}
\dfrac{1}{2} = \dfrac{6}{x}
\dfrac{1}{2} \, x = 6
x = 12 cm
Question 9 – here
80 people’s exercise patterns were recorded in one week.
The cumulative frequency graph gives information about the number of hours that these 80 people spent exercising in this week.
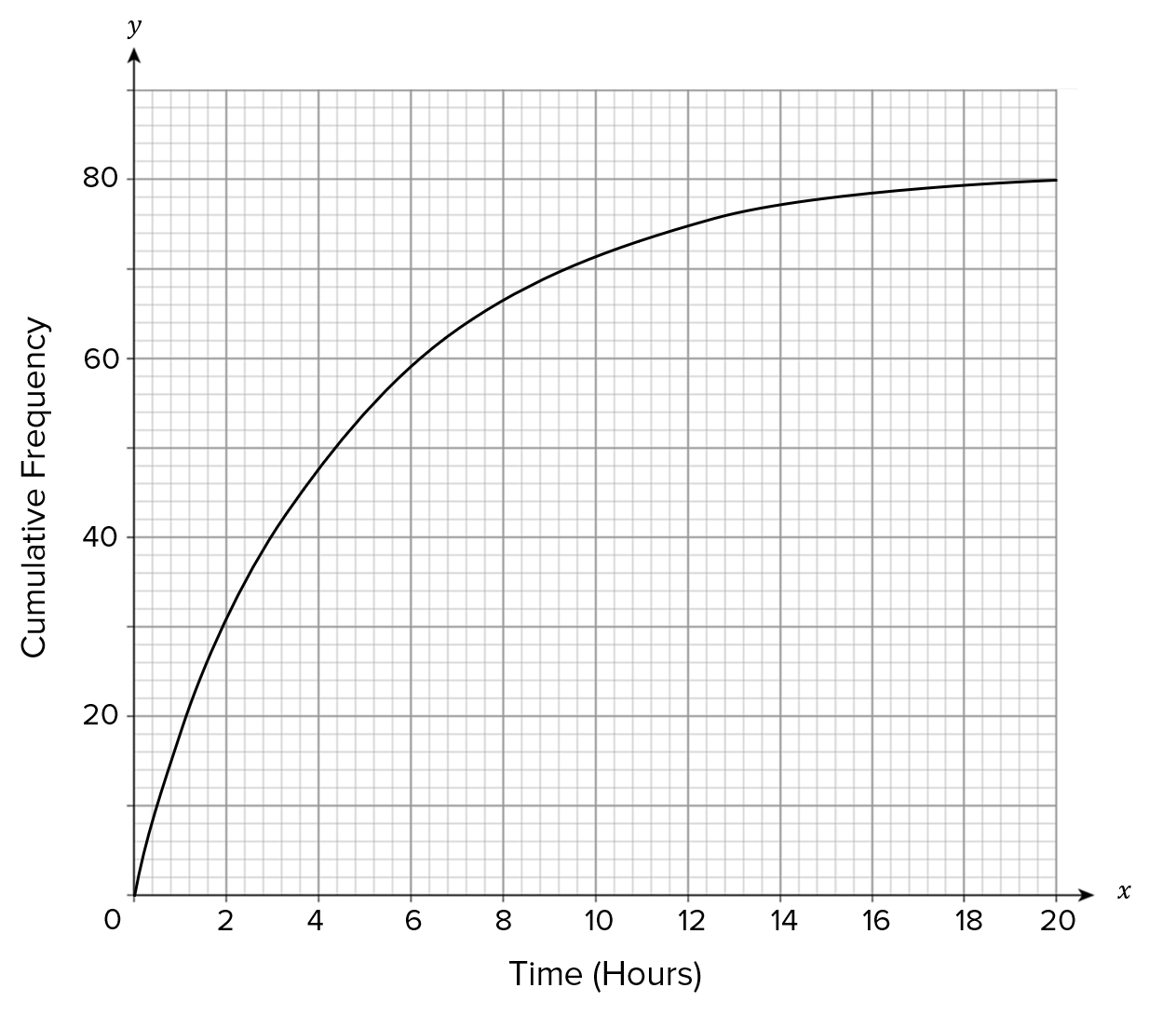
The shortest time spent exercising was 0 hours.
The longest time spent exercising was 16 hours.
Question 9(a) [3 marks]
Choose the box plot that is drawn correctly using the information above.
Answer type: Multiple choice type 1
A:
B:
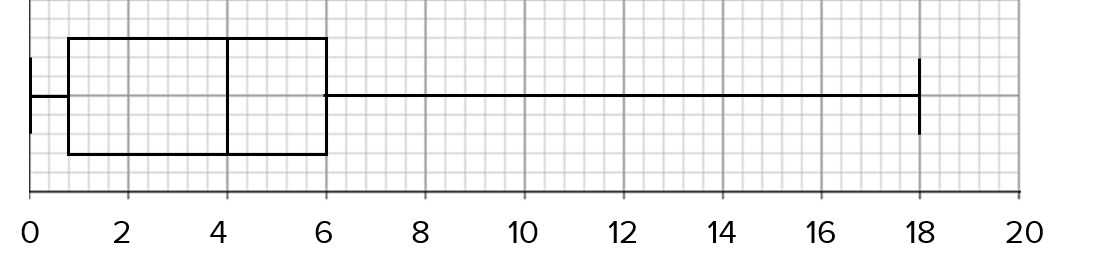
C:
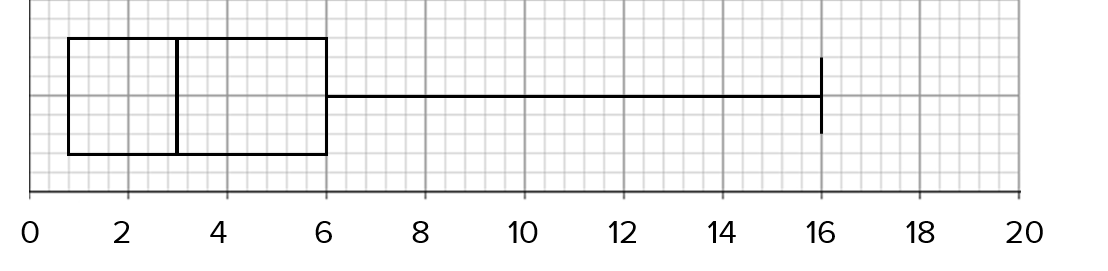
D:
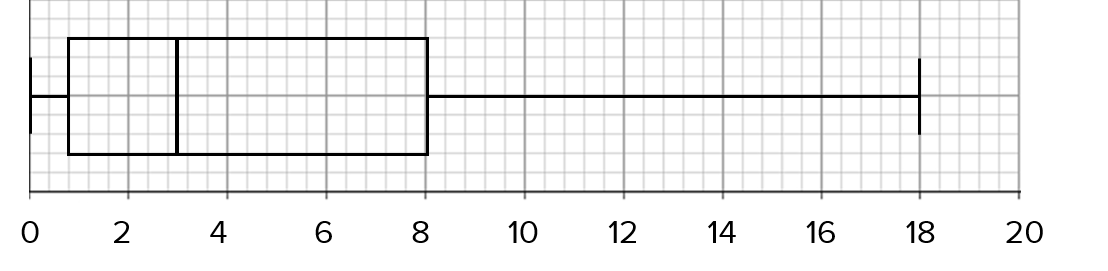
ANSWER: A
WORKING:
We have the largest and smallest value, for the whiskers of the box plot.
So, we need to find the lower quartile, the median and the upper quartile.
Since there are 80 people, the lower quartile is the 20th value, the median is the 40th value and the upper quartile is the 60th value.
We use the graph to find these values.
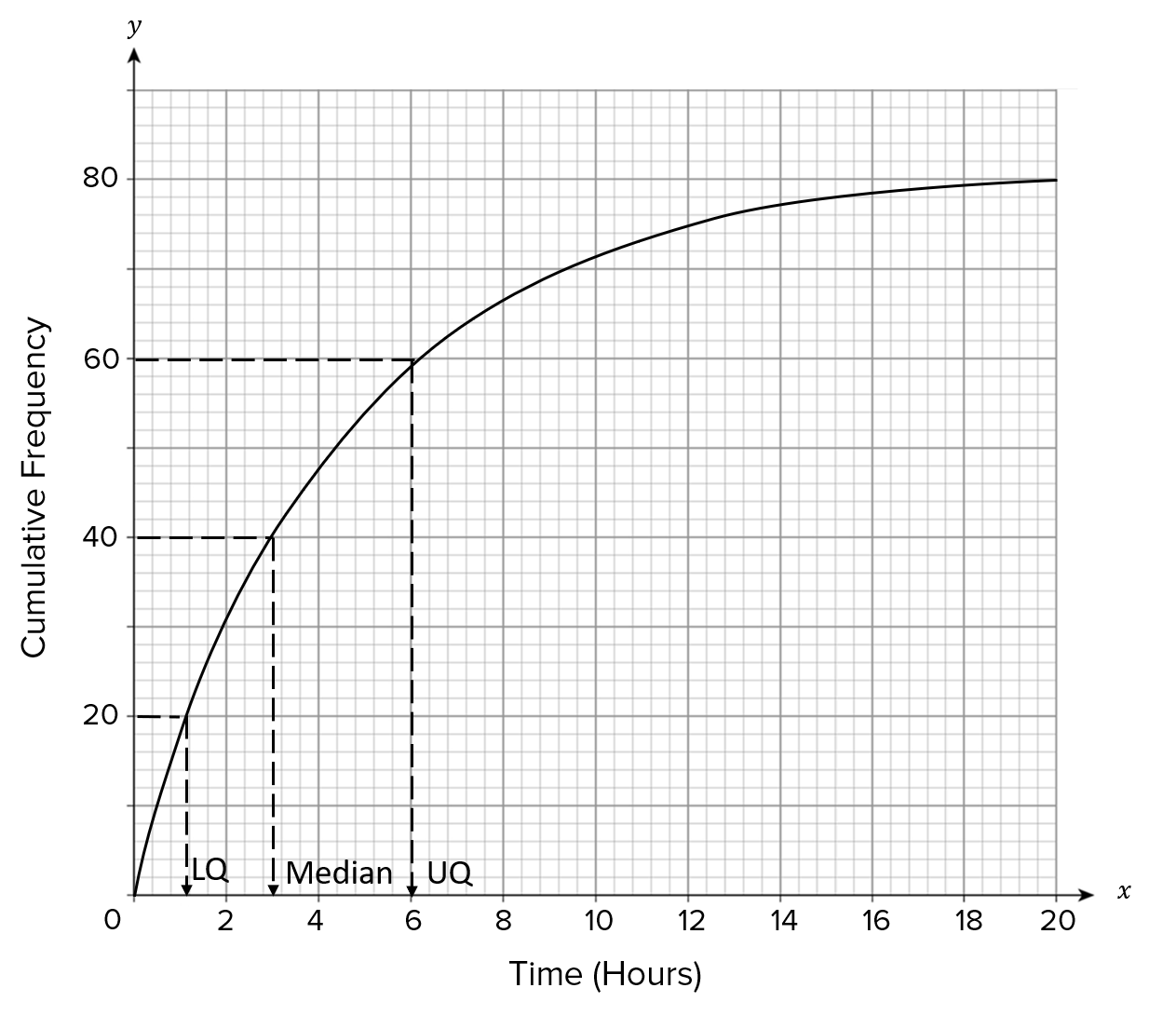
Hence, the lower quartile = 1, median = 3 and the upper quartile =6
We can then plot these on a box plot, together with the whiskers.
Question 9(b) [2 marks]
The next week, the same 80 people’s exercise patterns were recorded.
The box plot below shows information about the number of hours spent exercising on this next week.
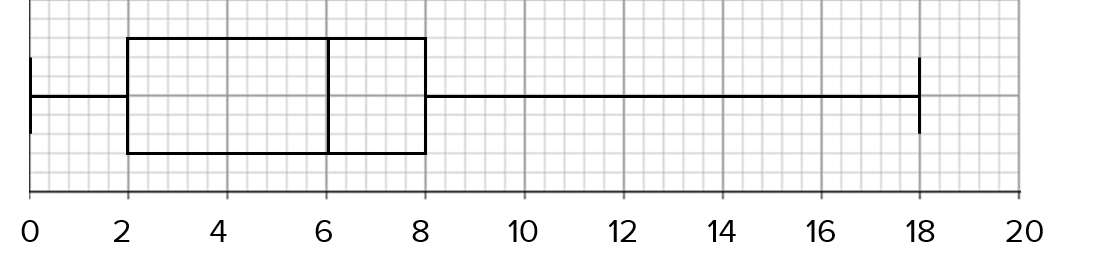
Choose the statement below that best describes the comparisons between the distribution of hours spent exercising on the first week with the second week.
Answer type: Multiple choice type 1
A: The median in the first week is lower than in the second week and the interquartile range in the first week is lower than in the second week.
B: The median in the first week is lower than in the second week and the interquartile range in the first week is greater than in the second week.
C: The median in the first week is greater than in the second week and the interquartile range in the first week is lower than in the second week.
D: The median in the first week is greater than in the second week and the interquartile range in the first week is greater than in the second week.
ANSWER: A
Question 9(c) [1 mark]
Susanne says,
“The longest number of hours spent exercising in the second week was 18 hours.
Therefore there must be some people who exercised for between 12 and 14 hours”
Is Susanne correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B
WORKING:
We don’t know the specific number of hours spent exercising, so there could be no people that exercise for between 12 and 14 hours.
Therefore, Susanne is not correct.
Question 10(a) [1 mark]
Simplify \dfrac{x + 2}{3(x+2)^2}
Answer type: Multiple choice
A: \dfrac{1}{3(x+2)}
B: \dfrac{1}{x+2}
C: \dfrac{x+2}{3}
D:\dfrac{1}{3}
ANSWER: A
WORKING:
\dfrac{x + 2}{3(x+2)^2} = \dfrac{x+2}{3(x+2)(x+2)} = \dfrac{1}{3(x+2)}
Question 10(b) [2 marks]
Factorise fully 48 - 3x^2
Answer type: Multiple choice
A: 3(4+x)(4-x)
B: 16 - x^2
C: 3(8+x)(8-x)
D: 45x^2
ANSWER: A
WORKING:
48 - 3x^2 = 3(16 - x^2) = 3(4+x)(4-x)
Question 11 [3 marks]
Jade and Henry work for a company that sells buckets of popcorn.
The company wants to have a special offer.
Here is Jade’s idea for the special offer.
Put 20\% more popcorn into each bucket and do not change the price.
Here is Henry’s idea for the special offer.
Reduce the price and do not change the amount of popcorn in each bucket.
Henry wants his idea to give the same value for money as Jade’s idea.
By what percentage, to the nearest whole number, does Henry need to reduce the price?
Answer type: Simple text answer
ANSWER: 17%
WORKING:
Make an assumption for e.g. 100g of popcorn = £6
Jade’s idea: 120g of popcorn = £6
So 100g of popcorn would be \dfrac{6}{1.2} = £5
Therefore Henry needs to reduce the price by £6 - £5 = £1
Percentage decrease = \dfrac{1}{6} \times 100 = 16.67 = 17 % (nearest whole number)
Question 12 [3 marks]

\textit{A,B} and \textit{C} are points of the circumference of a circle, centre \textit{O}.
\textit{DAE} is a tangent to the circle at \textit{A}.
What is the angle \textit{CAO} ?
Answer type: Simple text answer
ANSWER: 19 \degree
WORKING:

\angle\textit{BAO} = 90 - \angle\textit{BAE} = 90 - 62 = 28 \degree (radius meets tangent to circle at a right angle)
\angle\textit{OBA} = 28 \degree (isosceles triangle)
\angle\textit{CAD} = \angle\textit{CBO} + \angle\textit{OBA}= 43 + 28 = 71\degree (alternate segments)
\angle\textit{CAO} = 180 - \angle\textit{BAO} - \angle\textit{OBA} - \angle\textit{CAD} = 180 - 28 - 62 - 71 = 19 \degree (angles on a straight line)
Question 13 [2 marks]
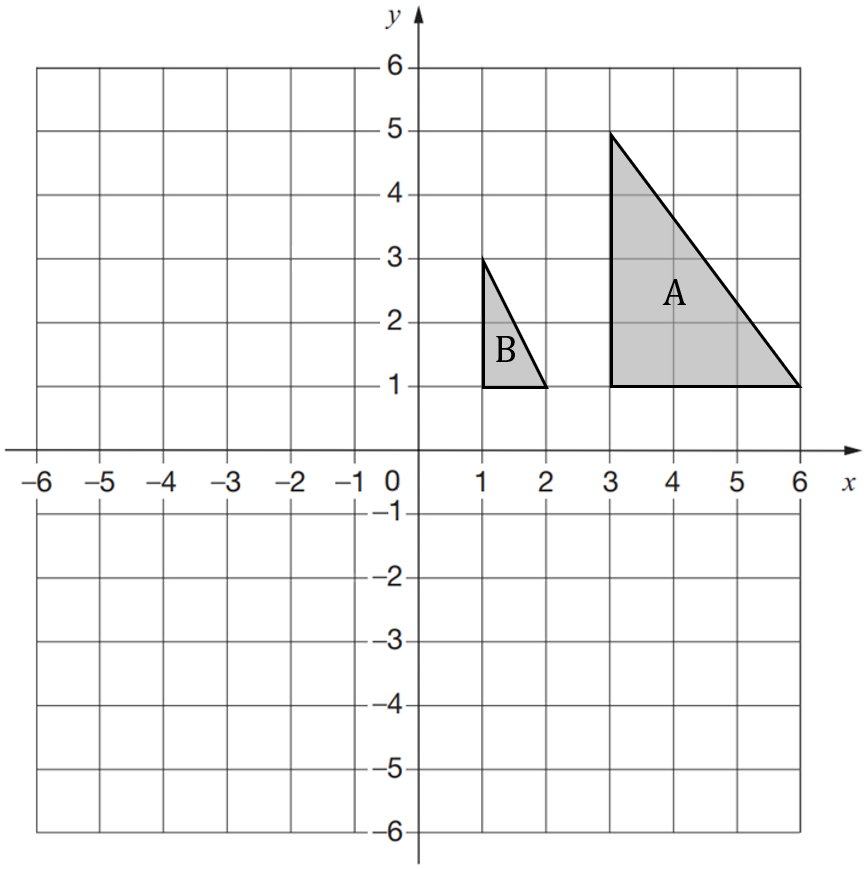
What is the single transformation that maps triangle A onto triangle B?
Answer type: Multiple choice
A: Enlargement by scale factor \dfrac{1}{2} from the point (-1,1)
B: Enlargement by scale factor 2 from the point (-1,1)
C: Enlargement by scale factor \dfrac{1}{2} from the point (-1,3)
D: Enlargement by scale factor 2 from the point (-1,5)
ANSWER: A
WORKING:
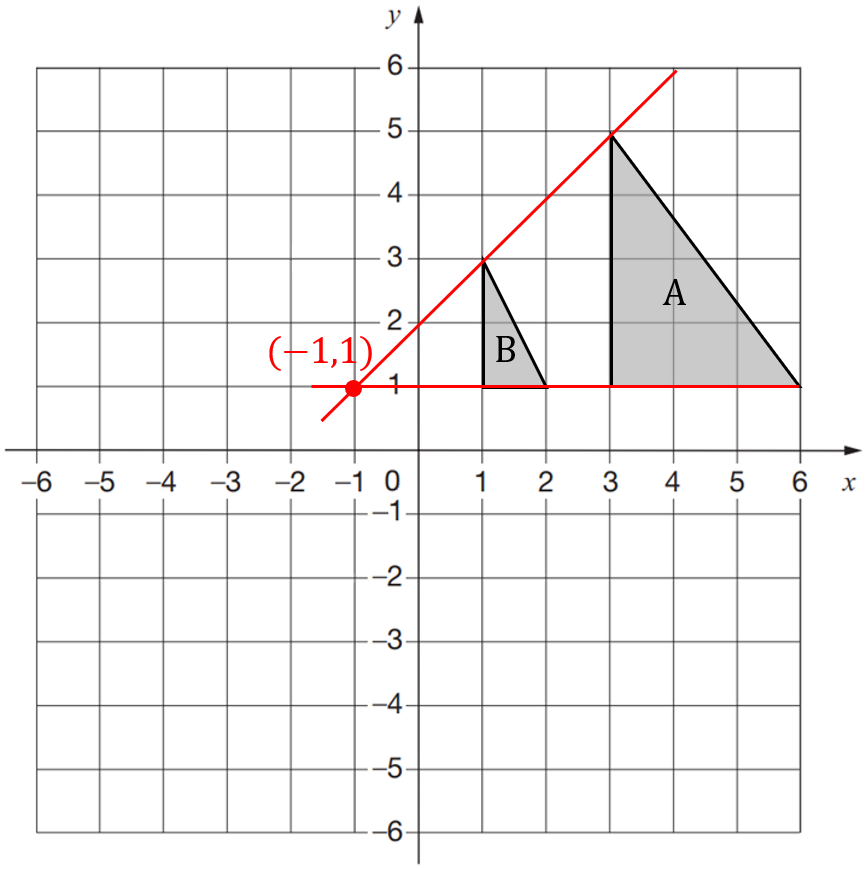
Question 14(a) [2 marks] – here
Find the value of \left( \dfrac{64}{125}\right)^\frac{2}{3}
Give your answer as a fraction in simplest form.
Answer type: Fraction
ANSWER: \dfrac{16}{25}
WORKING:
64^\frac{2}{3} = \left(\sqrt[3]{64}\right)^2 = 4^2 = 16
125^\frac{2}{3} = \left(\sqrt[3]{125}\right)^2 = 5^2 = 25
\left( \dfrac{64}{125}\right)^\frac{2}{3} = \dfrac{16}{25}
Question 14(b) [2 marks]
2^{x} = \dfrac{1}{16} \,\,\,\,\,\,\,\,\, 2^{y} = 4 \times \sqrt[3]{2} \,\,\,\,\,\, \,\,\,2^{z} = \dfrac{1}{\sqrt{4}}
Find the value of x + y - 2z
Answer type: Fraction
ANSWER: \dfrac{1}{3}
WORKING:
2^x = \dfrac{1}{16} = \dfrac{1}{2^4} = 2^{-4}
2^y = 4 \times \sqrt[3]{2} = 2^{2} \times 2^{\frac{1}{3}} = 2^{2 + \frac{1}{3}} = 2^{\frac{7}{3}}
2^z = \dfrac{1}{\sqrt{4}} = \dfrac{1}{2} = 2^{-1}
x = -4, \,\,\, y = \dfrac{7}{3}, \,\,\, z = -1
x + y - 2z = -4 + \dfrac{7}{3} - (-2) = -2 + \dfrac{7}{3} = -\dfrac{6}{3} + \dfrac{7}{3} = \dfrac{1}{3}
Question 15 [4 marks]
Three solid shapes A, B and C are similar.
The surface area of shape A is 9 cm^2
The surface area of shape B is 49 cm^2
The ratio of the volume of shape B to the volume of shape C is 64:125
What is the ratio of the height of shape A to the height of shape C?
Answer type: Multiple choice type 1
A: 12: 35
B: 3:5
C: 3:7
D: 4:5
ANSWER: A
WORKING:
A:B
Area scale factor = 9:49
Length scale factor = \sqrt{9}:\sqrt{49} = 3:7
B:C
Volume scale factor =64:125
Length scale factor = \sqrt[3]{64}:\sqrt[3]{125} = 4:5
A:B:C
\,3\,:\,\,\,7 \quad \quad \quad(\times 4)
\quad \,\,\,\,\,\,\, 4\,:\,\,5 \quad \,(\times 7)
12:28:35
So, A:C = 12:35
Question 16 [3 marks]
0.4\dot{7}\dot{6} can be written as which of the following fractions in simplest form?
Answer type: Multiple choice
A: \dfrac{236}{495}
B: \dfrac{347}{990}
C: \dfrac{495}{941}
D:\dfrac{472}{967}
ANSWER: A
WORKING:
Let x = 0.4\dot{7}\dot{6}
10x = 4.\dot{7}\dot{6}
1000x = 476.\dot{7}\dot{6}
990x = 1000x - 10x = 476.\dot{7}\dot{6} - 4.\dot{7}\dot{6} = 472
x = \dfrac{472}{990} = \dfrac{236}{495}
Question 17 [4 marks]
Below is a sketch of a curve.
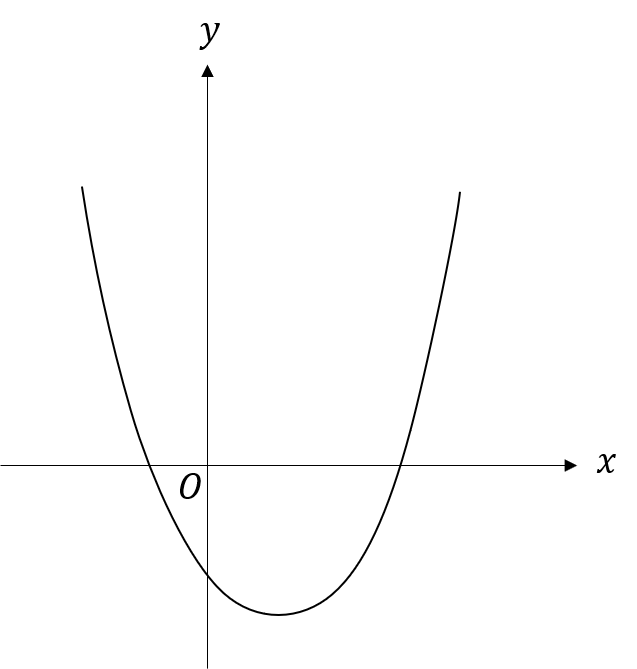
The equation of the curve is y = x^2 + ax + b where a and b are integers.
The points (0,-3) and (3,0) lie on the curve.
Find the x and y coordinates of the turning point of the curve.
Answer type: Multiple answers type 1
ANSWERS:
x = 1
y = -4
WORKING:
Substitute in (0,-3) into the equation of the curve.
-3 = 0^2 + a(0) + b
b = -3
Then, substitute in (3,0),
0 = 3^2 + a(3) + (-3)
0 = 9 + 3a -3
0 = 6 + 3a
3a = -6
a = -2
So, the equation of the curve is y = x^2 - 2x - 3
Finally, to find the turning point of the curve, we complete the square
y = (x-1)^2 - 1 - 3 y = (x-1)^2 - 4
So, the turning point of the curve is (1,-4)
Question 18(a) [1 mark]
The graph of y=f(x) is shown below.
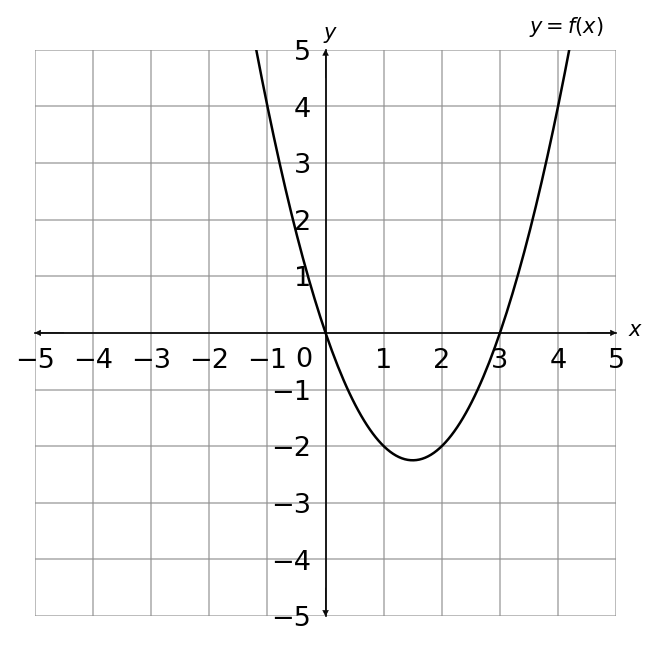
Choose the correct graph that sketches the graph of y = f(x+2)
Answer type: Multiple choice type 1
A:
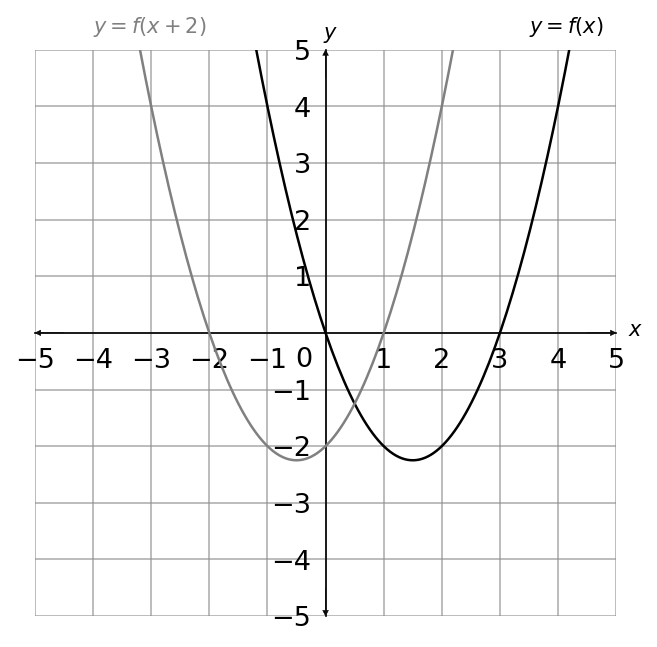
B:
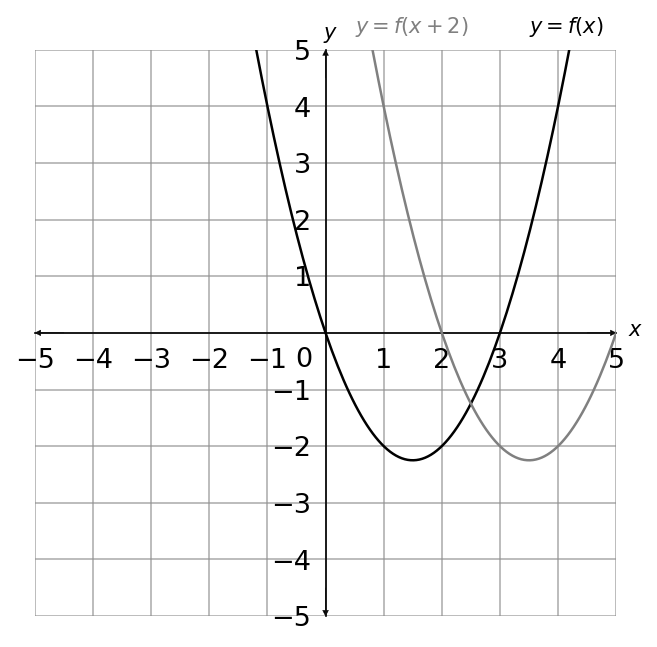
C:
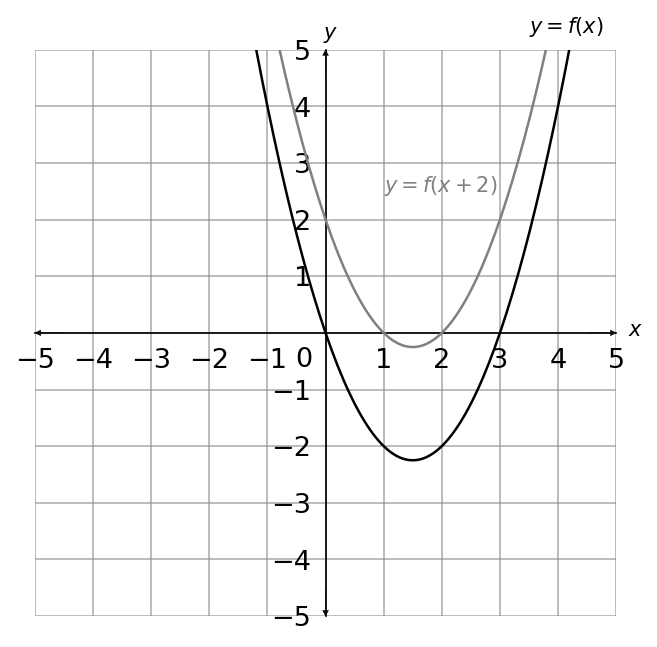
D:
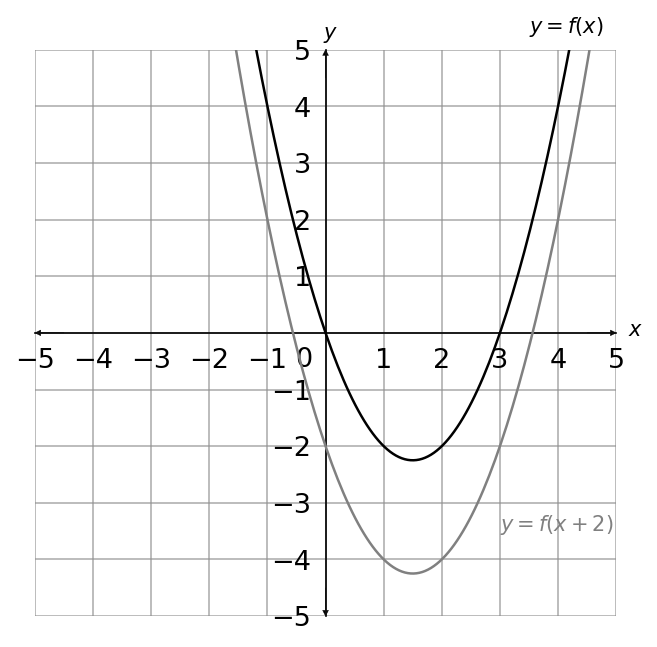
ANSWER: A
WORKING:
y=f(x+2) moves the graph 2 places to the left
Question 18(b) [2 marks]
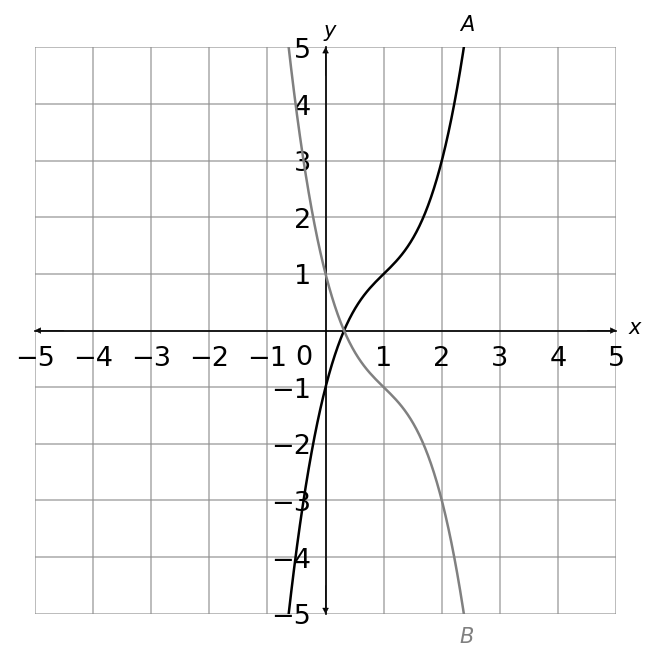
On the grid, graph A has been reflected to give graph B
Graph A has equation y = g(x)
What is the equation of graph B?
Answer type: Multiple choice type 1
A: y=- g(x)
B: y = g(-x)
C: y = -g(-x)
D: y = \dfrac{1}{g(x)}
ANSWER: A
WORKING:
Graph A has been reflected in the x axis to give graph B
Question 19
For the values of x
f(x) = (x+1)(x+3) and g(x) = 4(x - 2)
Question 19(a) [2 marks]
What is fg(x) in simplest form?
Answer type: Multiple choice
A: 16x^2 - 48x + 35
B: 4x^2 + 16x + 8
C: 16x^2 + 16x + 8
D: 4x^2 - 48x + 35
ANSWER: A
WORKING:
Substitute g(x) into f(x)
fg(x) = (4(x-2) + 1)(4(x-2) + 3)
= (4x - 7)(4x -5)
= 16x^2 - 48x + 35
Question 19(b) [2 marks]
What is g^{-1}(5)?
Answer type: Fraction
ANSWER: \dfrac{13}{4}
WORKING:
g^{-1}(x) = \dfrac{1}{4}(x) + 2
g^{-1}(5) = \dfrac{1}{4}(5) + 2 = \dfrac{13}{4}
Question 20 [3 marks]
Write \dfrac{3(\sqrt{50} - \sqrt{2})^2}{\sqrt{32}+4} in the form a(b + \sqrt{2}) where a and b are integers
Answer type: Multiple choice
A: 24(-1 + \sqrt{2})
B: 24(1 + \sqrt{2})
C: 32(-1 + \sqrt{2})
D: 32(2 + \sqrt{2})
ANSWER: A
WORKING:
\sqrt{50} = \sqrt{25}\sqrt{2} = 5\sqrt{2}
\sqrt{32} = \sqrt{16}\sqrt{2} = 4\sqrt{2}
\dfrac{3(5\sqrt{2}-\sqrt{2})^2}{4\sqrt{2}+4} = \dfrac{3(4\sqrt{2})^2}{4\sqrt{2} + 4} = \dfrac{3(32)}{4\sqrt{2} + 4} = \dfrac{96}{4\sqrt{2} + 4} =\dfrac{96}{4(\sqrt{2} + 1)} = \dfrac{24}{\sqrt{2} + 1}
\dfrac{24}{\sqrt{2} + 1} \times \dfrac{\sqrt{2} - 1}{\sqrt{2}-1} = 24\sqrt{2} - 24 = 24(-1 + \sqrt{2})
Question 21 [5 marks]
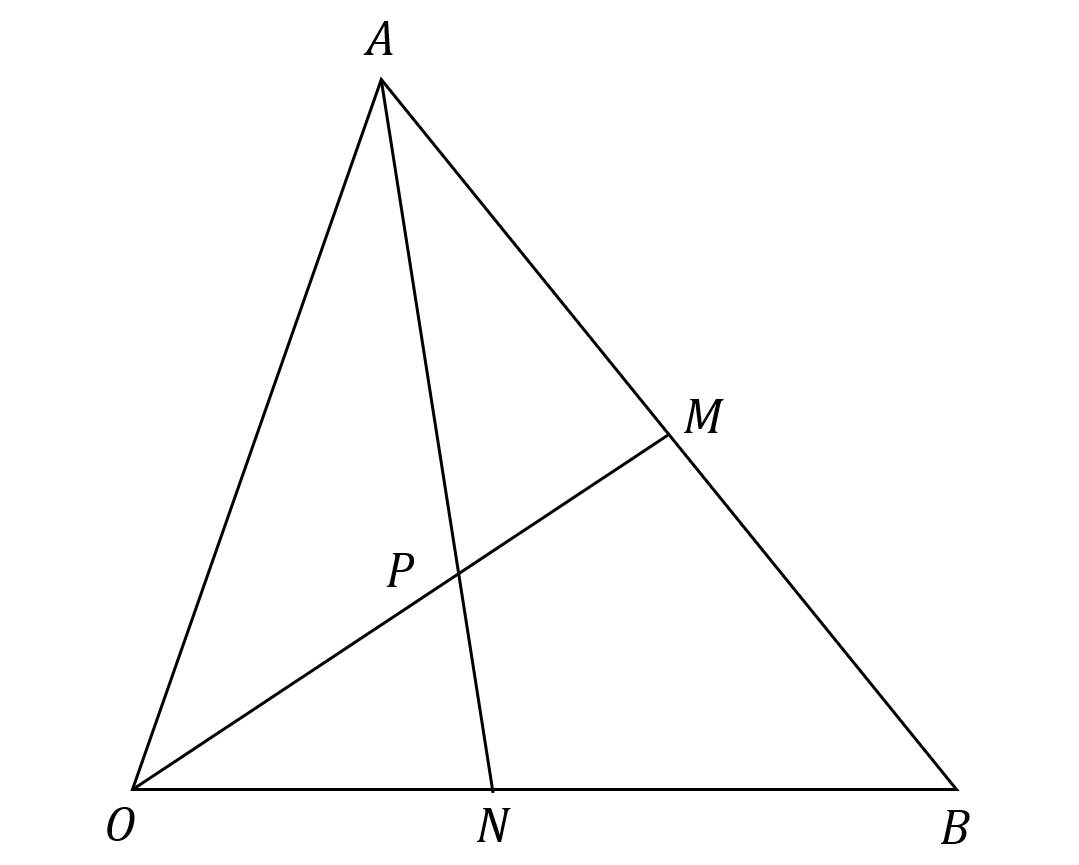
\textit{OAB} is a triangle.
\textit{OPM} and \textit{APN} are straight lines.
\textit{M} is the midpoint of \textit{AB}.
\overrightarrow{OA} = \textbf{a} and \overrightarrow{OB} = \textbf{b}
\textit{OP}:\textit{PM} = 4:3
What is the ratio \textit{ON}:\textit{NB} in simplest form?
Answer type: Multiple answers
ANSWER: \textit{ON} = 2 and \textit{NB} = 3
WORKING:
\overrightarrow{AB} = \overrightarrow{AO} + \overrightarrow {OB} = -\textbf{a} + \textbf{b}
\overrightarrow{OM} = \overrightarrow{OA} + \overrightarrow{AM} = \overrightarrow{OA} + \dfrac{1}{2}(\overrightarrow{AB}) = \textbf{a} + \dfrac{1}{2}(-\textbf{a} + \textbf{b}) = \dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}
\overrightarrow{AP} = \overrightarrow{AO} + \overrightarrow{OP} = -\textbf{a} + \dfrac{4}{7}(\overrightarrow{OM}) = -\textbf{a} + \dfrac{4}{7} \bigg(\dfrac{1}{2}\textbf{a} + \dfrac{1}{2}\textbf{b}\bigg) = -\textbf{a} + \dfrac{2}{7}\textbf{a} + \dfrac{2}{7}\textbf{b} = -\dfrac{5}{7}\textbf{a} + \dfrac{2}{7}\textbf{b} = \dfrac{5}{7} \bigg(-\textbf{a} + \dfrac{2}{5}\textbf{b}\bigg)
\overrightarrow{AN} = -\textbf{a} + k\textbf{b}
\overrightarrow{AP} and \overrightarrow{AN} are multiples since \textit{APN} is a straight line
Hence, k = \dfrac{2}{5}
\overrightarrow{ON} = \overrightarrow{OA} + \overrightarrow{AN} = \textbf{a} + \bigg(-\textbf{a} + \dfrac{2}{5}\textbf{b}\bigg) = \dfrac{2}{5}\textbf{b}
\overrightarrow{ON}:\overrightarrow{NB} = \dfrac{2}{5}:\dfrac{3}{5} = 2:3
Question 22 [6 marks]
There are only red sweets and yellow sweets in a packet.
There are 2 more red sweets than yellow sweets in the packet.
There are more than 5 sweets in the packet.
Amber is going to take at random two sweets from the packet.
The probability that Amber will take two sweets of the same colour is \dfrac{19}{40}
What is the number of yellow sweets in the packet?
Answer type: Simple text answer
ANSWER: 7
WORKING:
Yellow sweets = Y = x
Red sweets = R = x + 2
P(Y) = \dfrac{x}{2x + 2} and P(R) = \dfrac{x+2}{2x+2}
P(Y,Y) + P(R,R) = \dfrac{19}{40}
\bigg\{ \dfrac{x}{2x + 2} \times \dfrac{x-1}{2x+1}\bigg\} + \bigg\{\dfrac{x+2}{2x+2} \times \dfrac{x+1}{2x+1}\bigg\} = \dfrac{19}{40}
\dfrac{x(x-1)}{(2x+2)(2x+1)} + \dfrac{(x+2)(x+1)}{(2x+2)(2x+1)} = \dfrac{19}{40}
\dfrac{2x^2 + 2x + 2}{(2x + 2)(2x + 1)} = \dfrac{19}{40}
40(2x^2 + 2x + 2) = 19(2x + 2)(2x + 1)
80x^2 + 80x + 80 = 76x^2 + 114x + 38
4x^2 - 34x + 42 = 0
2x^2 - 17x + 21 = 0
(2x - 3)(x - 7) = 0
x = \dfrac{3}{2}, x = 7
As x > 5, x must be 7
Therefore the number of yellow sweets in the packet is 7
