Question 1
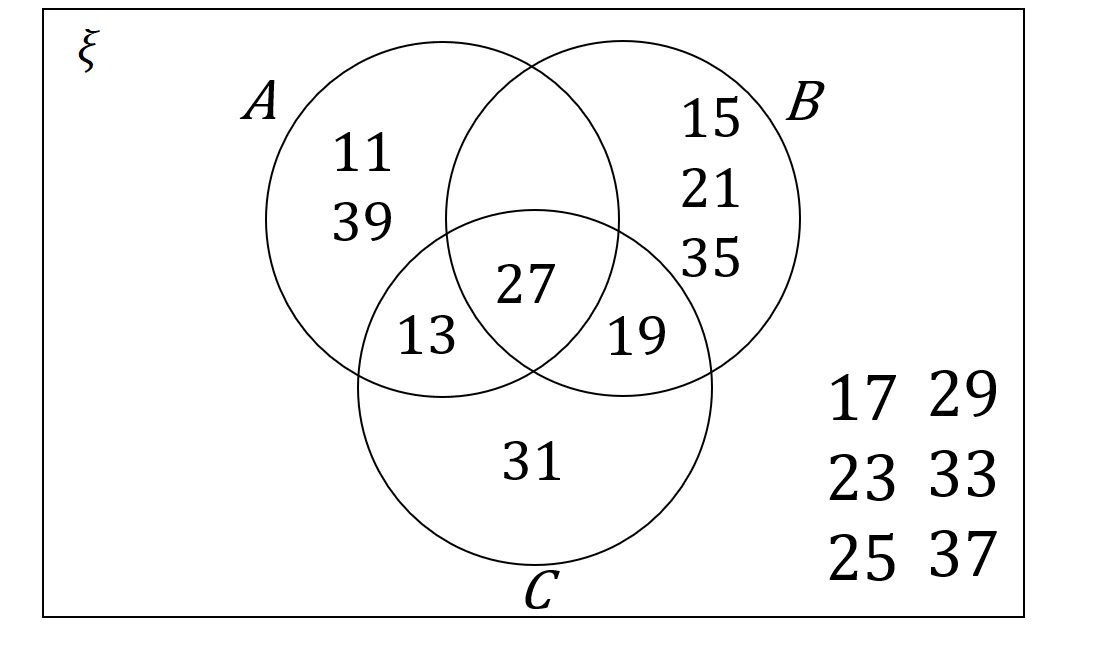
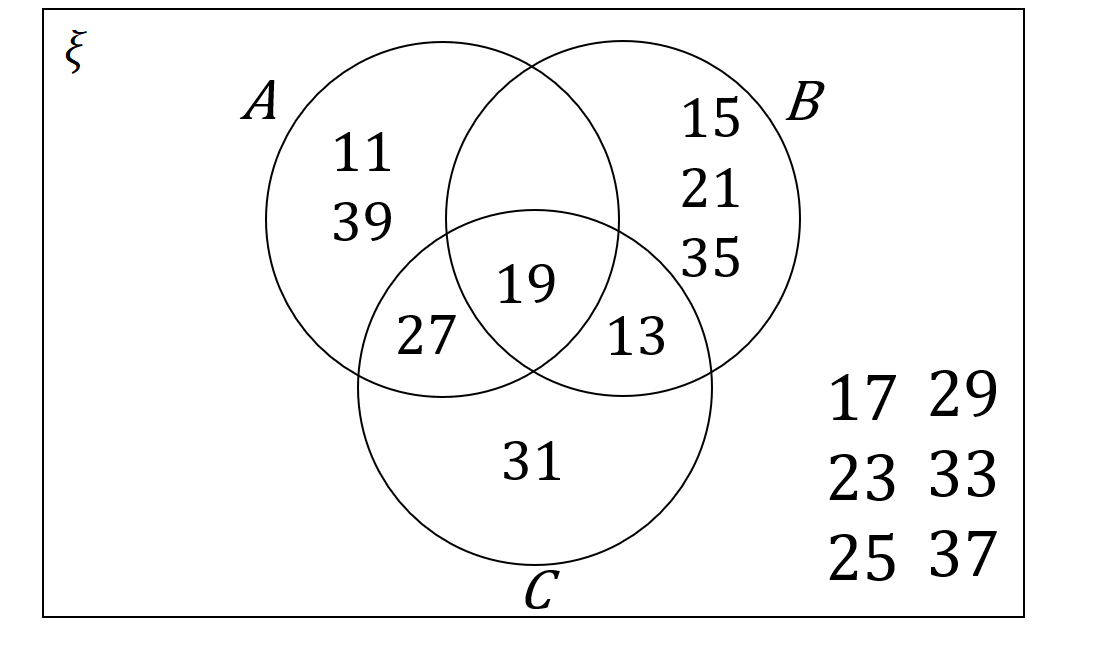
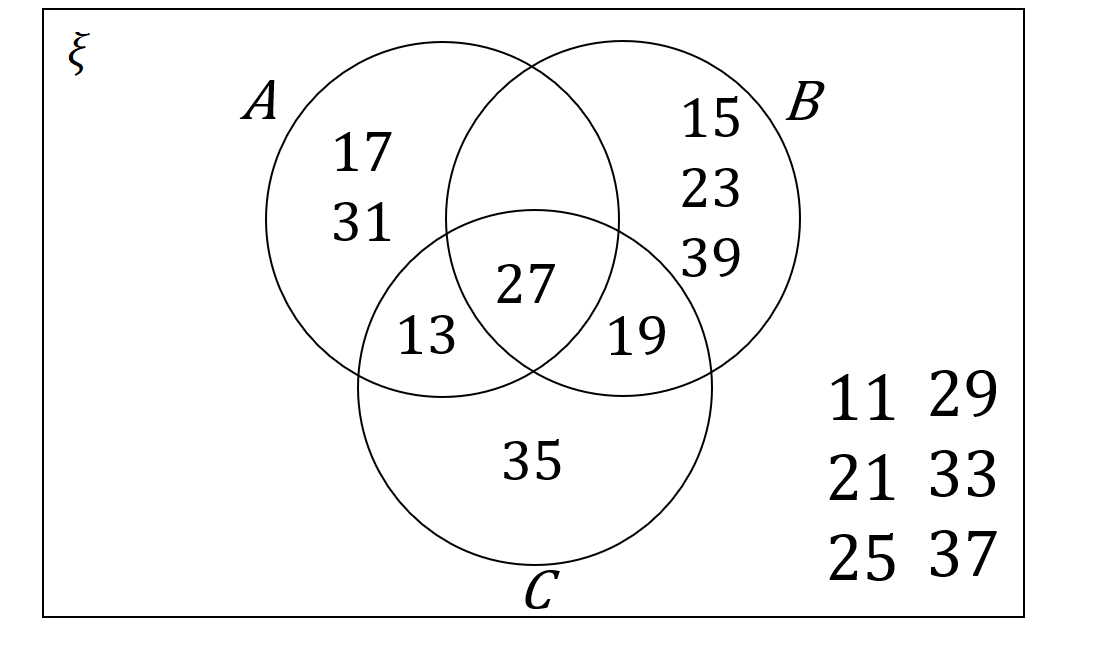
\xi = \{odd numbers between 10 and 40\}
\textit{A} = \{11,13,27,39\}
\textit{B} = \{15,19,21,27,35\}
\textit{C} = \{13,19,27,31\}
Question 1(a) [4 marks]
Which of the following Venn diagrams is correct?
Answer type: Multiple choice
A:
B:
C:
D:
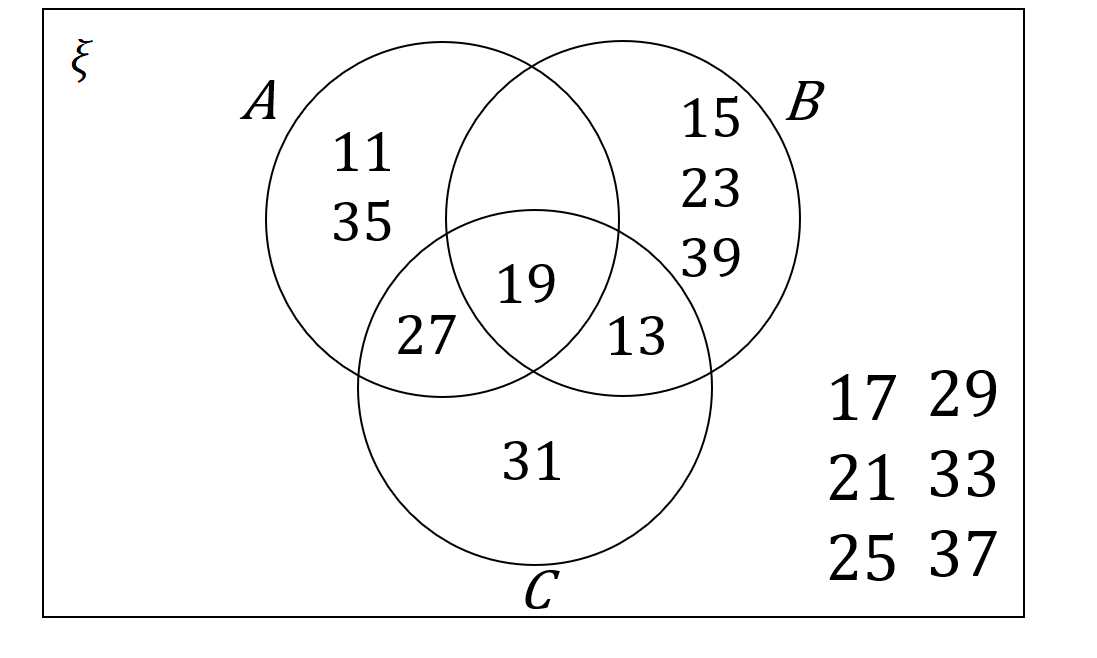
ANSWER: A
Question 1(b) [2 marks]
A number is chosen at random from \sigma.
Find the probability that the number is a member of A \cup C
Answer type: Fraction
ANSWER: \dfrac{6}{15}
WORKING:
A \cup C = A or C
The numbers that satisfy A or C are 11,13,19,27,31,39
There are a total of 15 numbers in \sigma
Probability =\dfrac{6}{15}
Question 2 [2 marks]
Michael has information about how many hours 10 students revised for their maths exam and the results they achieved.
He is asked to draw a scatter graph and a line of best fit for this information.
Here is his answer.

Michael has plotted the points accurately.
What is wrong with his answer?
Answer type: Multiple choice
A: The line of best fit is inaccurate.
B: The labels on the y axis are not linear.
C: There is no correlation between the time spent revising and the result achieved.
D: The time should start at 140 hours.
ANSWER: A
Question 3 [4 marks]
\textit{BEG} is a triangle.
\textit{ABC} and \textit{DEF} are parallel lines.

What is the size of angle x?
Answer type: Simple text answer
ANSWER: 52 \degree
WORKING:

\angle\textit{BEG} = 180 - \angle\textit{DEB} - \angle\textit{GEF} = 180 - 120 - 110 = 50 \degree
\angle\textit{ABE} + \angle\textit{DEB} = 180 \degree so = \angle\textit{ABE} = 180 - 120 = 60 \degree
\angle\textit{EBG} = 180 -\angle\textit{ABE} - \angle\textit{CBG} = 180 - 60 - 42 = 78 \degree
\angle\textit{BGE} = 180 - \angle\textit{BEG} - \angle\textit{ABE} = 180 - 50 - 78 =52 \degree
So, x = 52 \degree
Question 4
Southern Bank has two types of account.
Both accounts pay compound interest.
Savings account: Interest 3\% per annum
Shares account: Interest 4.5\% per annum
Amy invests £3500 in the savings account.
Barney invests £2100 in the shares account.
Question 4(a) [4 marks]
How much more interest will Amy get than Barney by the end of 3 years?
Answer type: Multiple choice
A: £28.05
B: £82.50
C: £25.08
D: £52.80
ANSWER: A
WORKING:
Amy:
3500 \times 1.03^3 = £3824.54 (nearest penny)
Interest = £3824.54 - £3500 = £324.54
Barney:
2100 \times 1.045^3 = £2396.45 (nearest penny)
Interest = £2396.45 - £2100 = £296.45
Difference = £324.54 - £296.45 = £28.09
Question 4(b) [1 mark]
In the 3rd year, the rate of interest for the savings account is changed to 3.5\% per annum.
Would Amy still get the most interest by the end of 3 years?
Answer type: Multiple choice
A: Yes
B: No
ANSWER: A
WORKING:
Amy already gets the most interest and so increasing her interest to 3.5\% will only make her get even more.
Question 5 [5 marks]
The diagram shows a floor in the shape of a trapezium.

James is going to varnish the floor.
Each 8 litre tin of varnish costs £21.49
1 litre of varnish covers an area of 5 m^2
James has £130 to spend on varnish.
How much more money would James need to buy all the varnish required to varnish the whole floor?
Answer type: Simple text answer
ANSWER: £20.43
WORKING:
Area of the trapezium =\dfrac{1}{2}(18+25) \times 12 = 258 m^2
As 1 litre of varnish is 5 m^2, 1 tin of varnish covers an area of 8 \times 5 = 40 m^2
\dfrac{258}{40} = 6.45, so James needs 7 tins
Total cost = 7 \times 21.49 = £150.43
Money needed = 150.43 - 130 = £20.43
Question 6 [3 marks]
\textit{A} is the point with coordinates (4, 19)
\textit{B} is the point with coordinates (7,z)
The gradient of the line \textit{AB} is 5
What is the value of z?
Answer type: Simple text value
ANSWER: 34
WORKING:
Gradient of \textit{AB} = \dfrac{\text{Change in } y}{\text{Change in } x} = \dfrac{z - 19}{7 - 4} = \dfrac{z - 19}{3} = 5
Rearrange to get
z - 19 = 15
z = 34
Question 7(a) [1 mark]
What is the number 0.0000031897 in standard form?
Answer type: Multiple choice
A: 3.1897 \times 10^{-6}
B: 31.897 \times 10^{-6}
C: 3.1897 \times 10^{-5}
D: 31.897 \times 10^{-7}
ANSWER: A
Question 7(b) [2 marks]
What is the number \dfrac{2.4 \times 10^{4} - 1.5 \times 10^{-3}}{3.1 \times 10^{-2}} in standard form, correct to 4 significant figures?
Answer type: Multiple choice
A: 7.742 \times 10^5
B: 77.72 \times 10^3
C: 7.742 \times 10^7
D: 777.4 \times 10^4
ANSWER: A
WORKING:
\dfrac{2.4 \times 10^{4} - 1.5 \times 10^{-3}}{3.1 \times 10^{-2}} = 774193.5
774193.5 = 774200 (4 sf)
774200 = 7.742 \times 10^5 in standard form
Question 8 [3 marks]
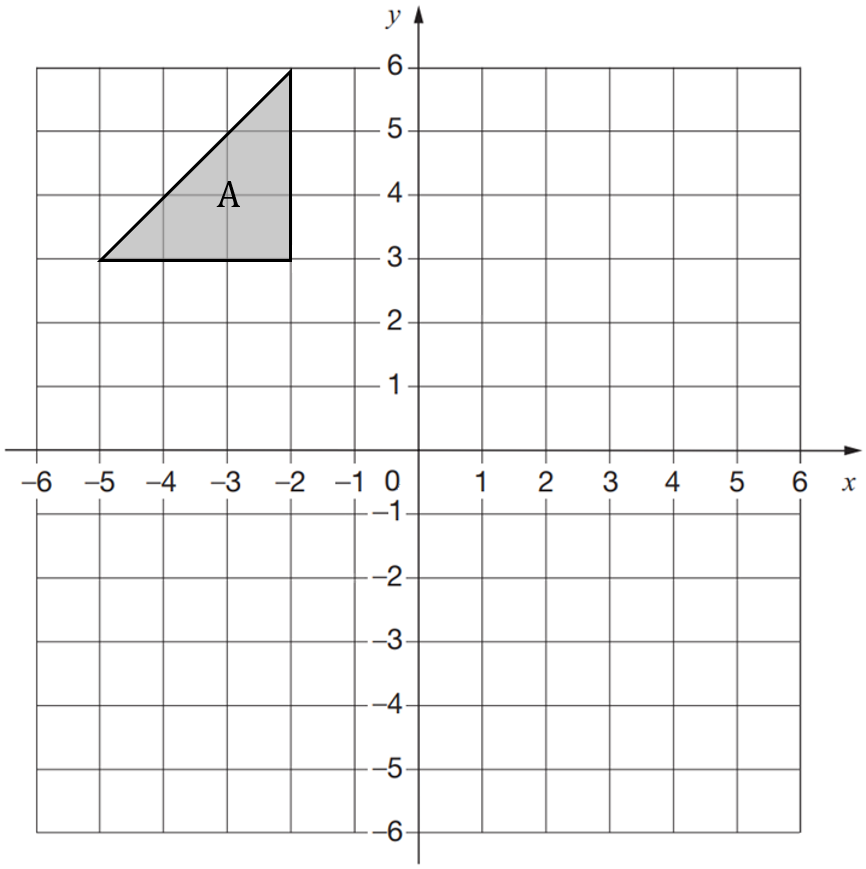
Triangle A is reflected in the line y = 1 to give triangle B
Triangle B is reflected in the line y = -x to give triangle C
Where will triangle C be located on the graph?
Answer type: Multiple choice
A:
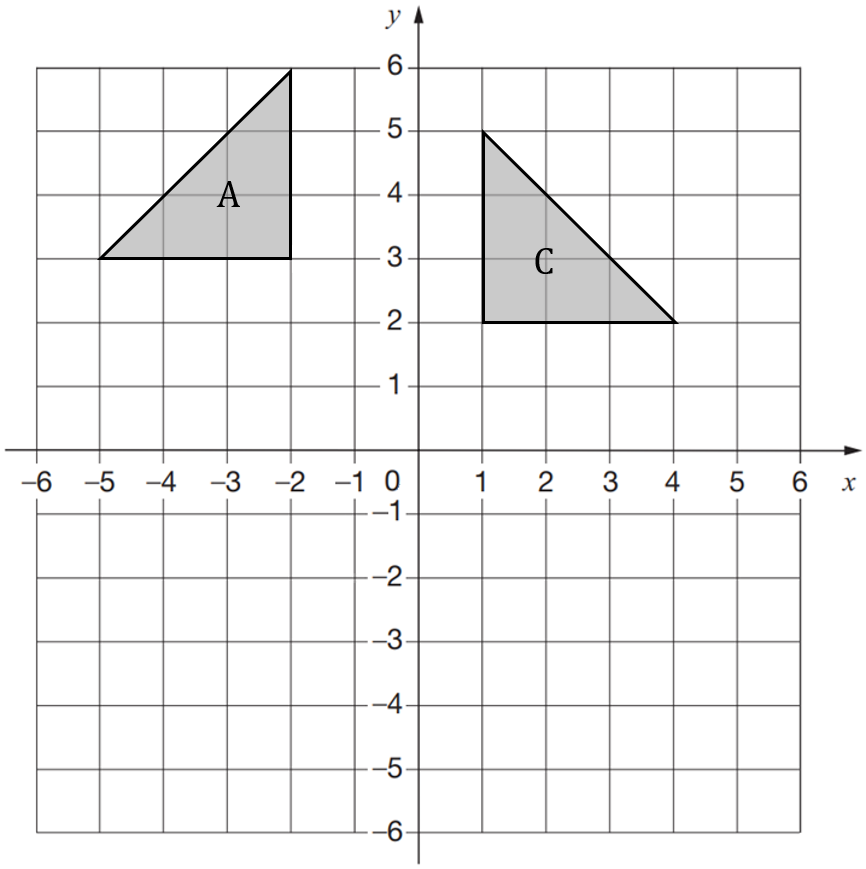
B:
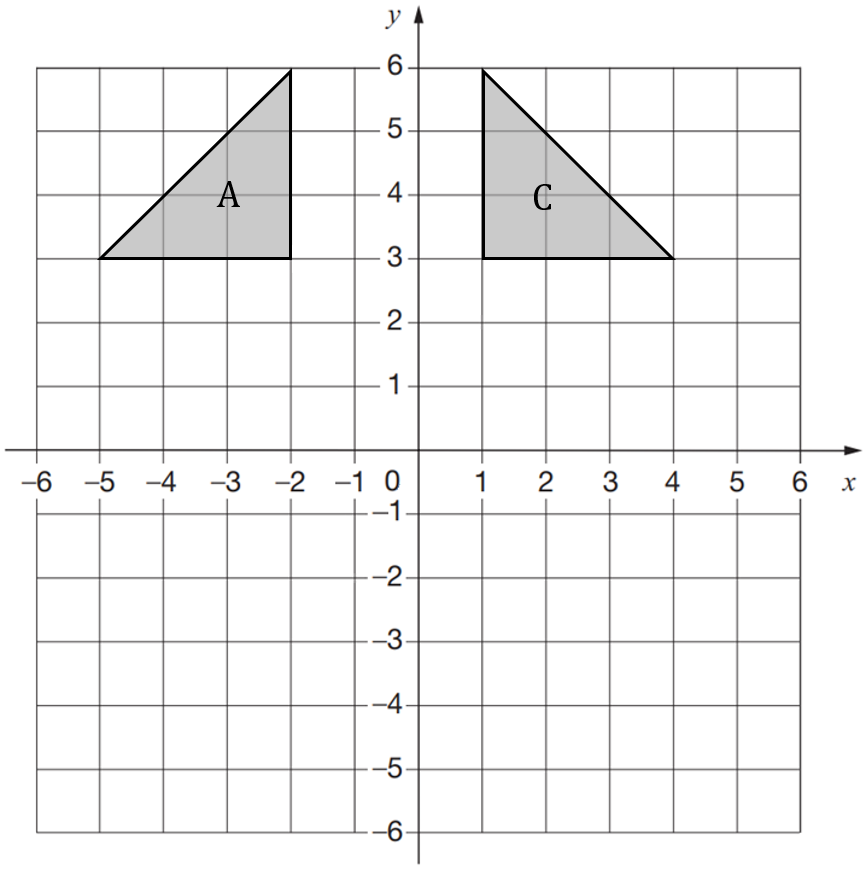
C:
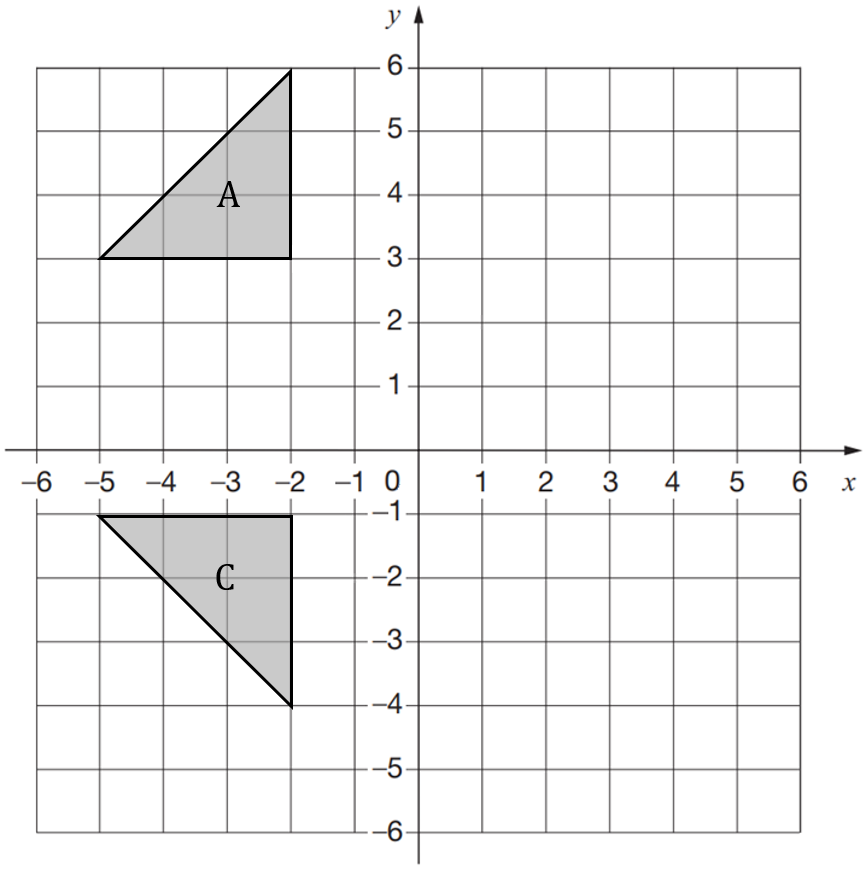
D:
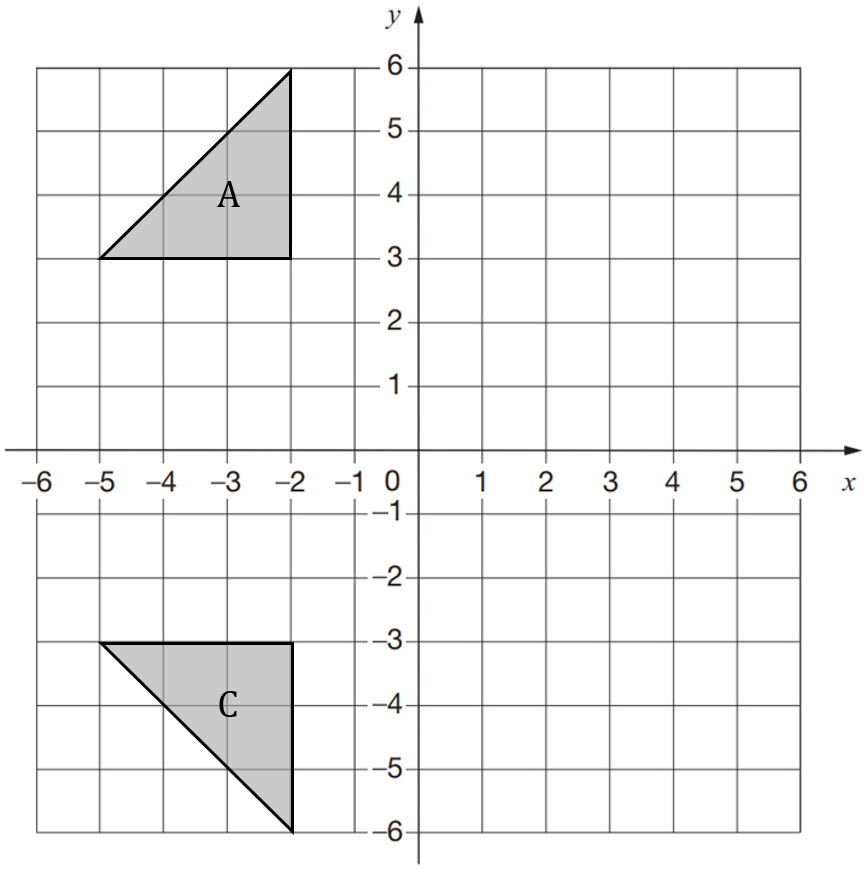
ANSWER: A
WORKING:
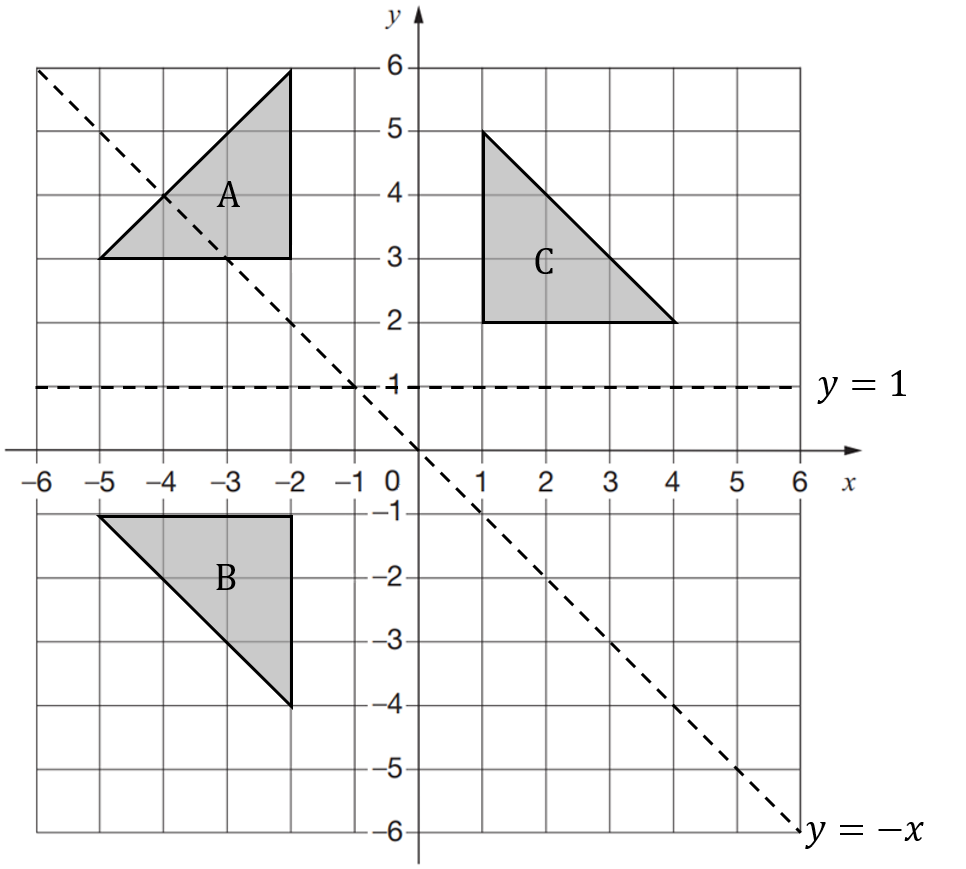
Question 9 [2 marks]
Laura truncates the number \textit{N} to 2 digits.
The result is 3.4
What is the error interval for \textit{N}?
Answer type: Multiple choice
A: 3.4 \leq \textit{N} < 3.5
B: 3.4 \leq \textit{N} < 4.4
C: 3.4 < \textit{N} < 4
D: 3.4 < \textit{N} < 3.5
ANSWER: A
WORKING:
Truncate means we limit the number of digits right of the decimal point without rounding.
Question 10 [5 marks] – here
Eleanor makes 80 litres of orange paint by mixing litres of red paint and litres of yellow paint.
The ratio of red paint to yellow paint is 3:7
Red paint is sold in 6 litre tins and each tin of red paint costs £32
Yellow paint is sold in 14 litre tins and each tin of yellow paint costs £60
Eleanor sells all the orange paint she makes in 10 litre tins.
She sells each tin of orange paint for £74.25
What will be Eleanor’s percentage profit on each tin of orange paint she sells, rounded to the nearest whole number?
Answer: Simple text answer
ANSWER: 61\%
WORKING:
Profit = Income - Cost
Cost:
Number of parts in ratio = 3 + 7 = 10
1 part = \dfrac{80}{10} = 8 litres
8 \times 3 = 24 litres of red paint
\dfrac{24}{6} = 4 tins of red paint
Red paint cost = 4 \times £32 = £128
8 \times 7 = 56 litres of yellow paint
\dfrac{56}{14} = 4 tins of yellow paint
Yellow paint cost = 4 \times £60 = £240
Total cost = £128 + £240 = £368
Income:
\dfrac{80}{10} = 8 tins of orange paint
Income = 8 \times £74.25= £594
Profit = 594 - 368 = £226
Percentage profit = \dfrac{226}{368} \times 100 = 61.4130435 = 61 \% (nearest whole number)
Question 11 [3 marks]
In a coffee shop there are
- 6 types of coffee
- 14 types of panini
- 12 types of cake
Charlotte is going to order one of the following combinations
- A coffee and a panini
- A panini and a cake
- A coffee, a panini and a cake
How many different ways are there for Charlotte to choose her order?
Answer type: Simple text answer
ANSWER: 1240 ways
WORKING:
6 \times 14 = 84 ways for Charlotte to order a coffee and a panini
14 \times 12 = 168 ways for Charlotte to order a panini and a cake
6 \times 14 \times 12 = 1008 ways for Charlotte to order a coffee, a panini and a cake
Total number of ways = 84 + 168 + 1008 = 1240
Question 12(a) [3 marks]
What is \dfrac{9x^2 - 25}{6x + 10} \times \dfrac{3x}{x^2 + 5x} in the form \dfrac{ax+b}{cx+d} where a,b,c and d are integers?
Answer type: Multiple choice
A: \dfrac{9x-15}{2x+10}
B: \dfrac{2x+10}{9x+15}
C: \dfrac{3x+5}{2x+10}
D: \dfrac{3x}{6x+5}
ANSWER: A
WORKING:
\dfrac{(3x + 5)(3x - 5)}{2(3x + 5)} \times \dfrac{3x}{x(x+5)}
= \dfrac{3x - 5}{2} \times \dfrac{3}{x+5}
= \dfrac{9x-15}{2x+10}
Question 12(b) [3 marks]
What is \dfrac{5}{x + 3} - \dfrac{1}{x + 4} - \dfrac{2}{x} as a single fraction?
Answer type: Multiple choice
A: \dfrac{2x^2 + 3x - 24}{x(x+3)(x+4)}
B: \dfrac{8x^2 + 37x + 24}{x(x+3)(x+4)}
C: \dfrac{4x^2 + 9x - 24}{x(x+3)(x+4)}
D: \dfrac{6x^2 + 31x + 24}{x(x+3)(x+4)}
ANSWER: A
WORKING:
\dfrac{5(x+4)(x)}{(x+3)(x+4)(x)} - \dfrac{1(x+3)(x)}{(x+3)(x+4)(x)} - \dfrac{2(x+3)(x+4)}{(x+3)(x+4)(x)}
=\dfrac{(5x^2 + 20x) - (x^2 + 3x) - (2x^2 + 14x + 24)}{x(x+3)(x+4)}
=\dfrac{2x^2 + 3x - 24}{x(x+3)(x+4)}
Question 13 [3 marks]
The diagram shows a circle and an equilateral triangle.
One side of the equilateral triangle is the diameter of the circle.
The circle has a circumference of 32 cm
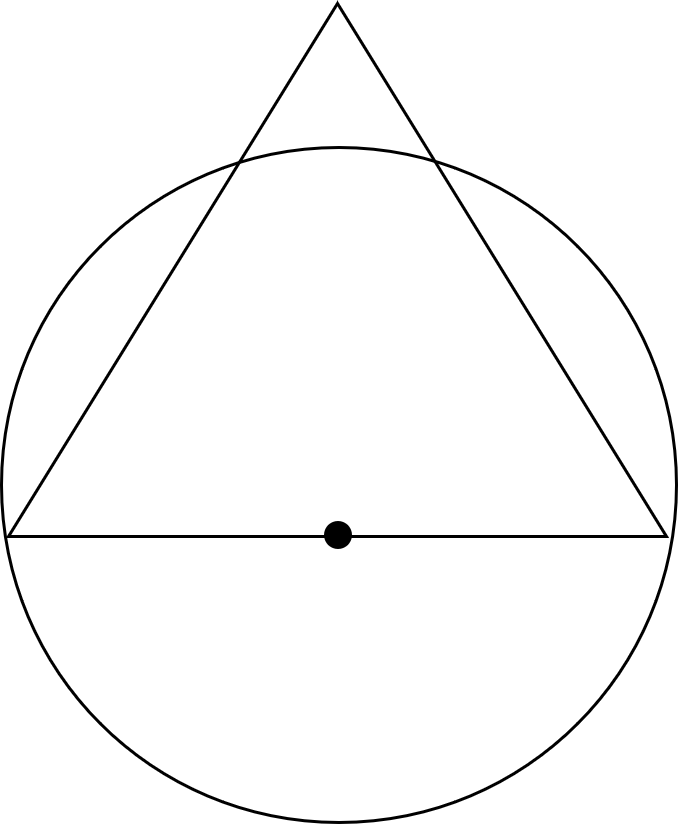
What is the area of the triangle?
Give your answer correct to 3 significant figures.
Answer type: Simple text answer
ANSWER: 44.9 cm^2
WORKING:
c = 32 = \pi d, so d = \dfrac{32}{\pi}
All the angles of the triangle are 60^\circ because it is an equilateral triangle
Area = \dfrac{1}{2} \times \dfrac{32}{\pi} \times \dfrac{32}{\pi} \times \sin 60 = 44.926 = 44.9 cm^2 (3 sf)
Question 14 [2 marks]
What is the graph with equation x + y = 3?
Answer type: Multiple choice
A:
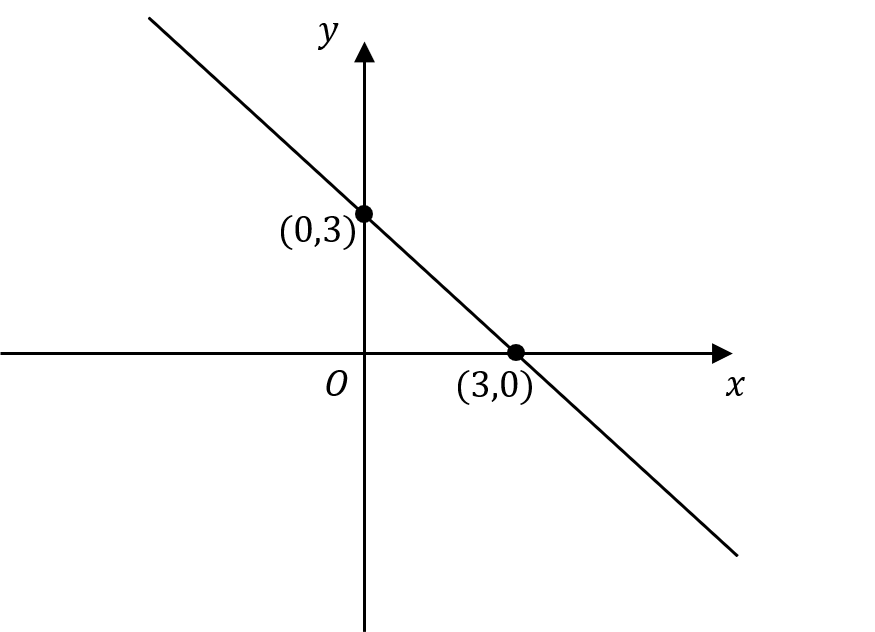
B:
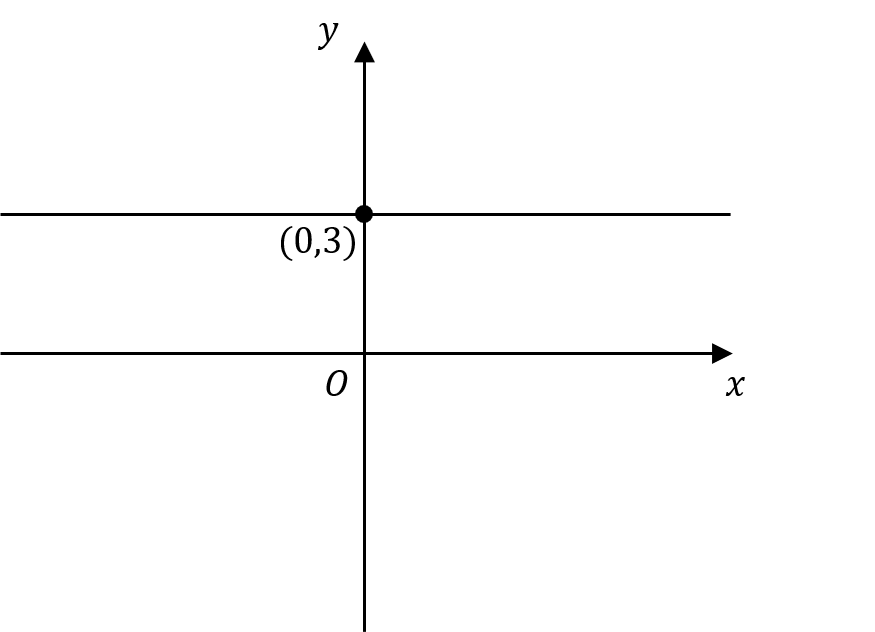
C:
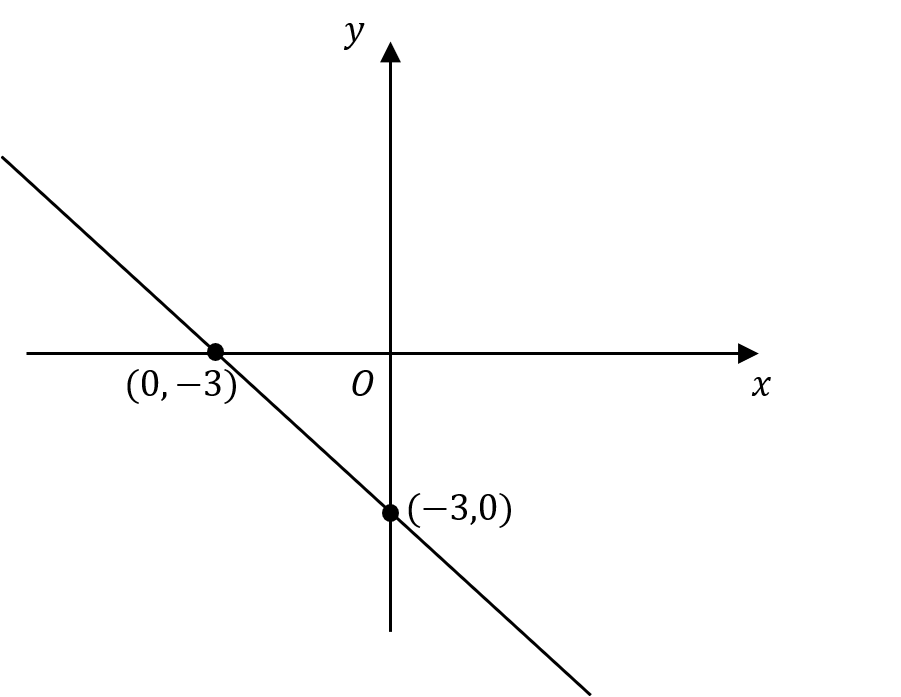
D:
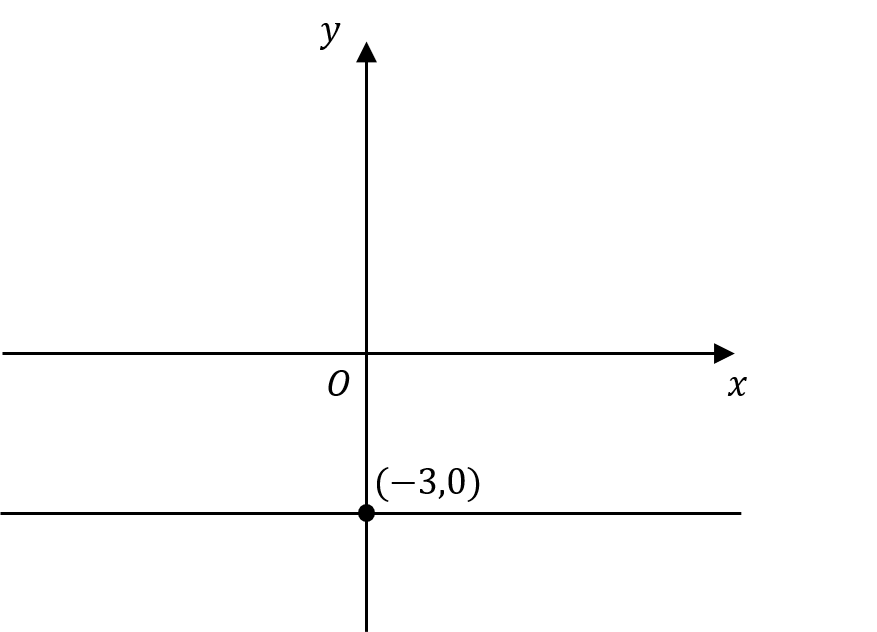
ANSWER: A
Question 15 [1 mark]
The equation of a circle is x^2 + y^2 = 110.25
What is the diameter of the circle?
Answer type: Simple text answer
ANSWER: 21
WORKING:
r^2 = 110.25
r = \sqrt{110.25} = 10.5 (r is positive)
d = 2r = 2 \times 10.5 = 21
Question 16
There are only black pens and red pens in a box.
Jack takes a random pen from the box.
The probability that the pen is black is 0.45
Jack puts the pen back in the box.
Molly takes a random pen from the box.
She puts the pen back in the box.
Question 16(a) [2 marks]
What is the probability that the pen Jack and Molly took out was the same colour?
Answer type: Simple text answer
ANSWER: 0.505
WORKING:
P_{(B,B)} = 0.45 \times 0.45 = 0.2025
P_{(R,R)} = 0.55 \times 0.55 = 0.3025
P_{(B,B)} + P_{(R,R)} = 0.2025 + 0.3025 = 0.505
Question 16(b) [2 marks]
There are 77 red pens in the box.
How many black pens are there in the box?
Answer type: Simple text answer
ANSWER: 63
WORKING:
\dfrac{77}{0.55} = 140 total pens
140 - 77 = 63 black pens
Question 17 [5 marks]
a and b are two numbers such that a > b
When you add 4 to a and add 4 to b the answers are in the ratio 2:1
When you subtract 6 from a and subtract 6 from b the answers are in the ratio 5:2
What is the ratio a:b in its simplest form?
Answer type: Multiple answers
ANSWER: a = 28, b = 13
WORKING:
a + 4:b + 4 = 2:1
\dfrac{a+4}{b+4} = \dfrac{2}{1}
1(a+4) = 2(b+4)
a + 4 = 2b + 8 , so a - 2b = 4
a - 6:b - 6 = 5:2
\dfrac{a-6}{b-6} = \dfrac{5}{2}
2(a-6) = 5(b-6)
2a - 12 = 5b - 30 so 2a - 5b = -18
Treat a - 2b = 4 and 2a - 5b = -18 as simultaneous equations and solve
2a - 4b = 8 \quad \quad\,\, (1)
2a - 5b = -18 \quad (2)
Subtract (2) from (1) to get b = 26
Substitute b = 26 into (1):
a - 2(26) = 4 so a = 56
The ratio is 56:26 = 28:13
So, a = 28, b = 13
Question 18 [4 marks]
The straight line L_{1} passes through the points with coordinates (4,2) and (6,7)
The straight line L_{2} passes through the origin and has gradient \dfrac{3}{2}
The lines L_1 and L_2 intersect at the point P.
What are the coordinates of P ?
Answer type: Multiple answers
ANSWER: x = 8, y = 12
WORKING:
L_{1} : M = \dfrac{\text{Change in } y}{\text{Change in } x} = \dfrac{7-2}{6-4} = \dfrac{5}{2}
y = \dfrac{5}{2}x + c
2 = \dfrac{5}{2}(4) + c
c = 2 - 10 = -8
So, y = \dfrac{5}{2}x - 8
L_{2} : y = \dfrac{3}{2}x
As L_{1} and L_{2} intersect at point \textit{P}, the values of x and y are the same.
So, we have two simultaneous equations, that we can solve as follows
\dfrac{5}{2}x - 8 = \dfrac{3}{2}x
x = 8
Substitute x=8 into the equation of L_2 to get
y = \dfrac{3}{2}x = \dfrac{3}{2}(8) = 12
Hence, x = 8, y = 12
Question 19 [5 marks]
Solve 5 < \dfrac{m^4 + 9}{5} < 18
Answer type: Multiple choice
A: 2 < m < 3 and -3 < m < -2
B: 2 < m < 3
C: 16 < m < 81
D: 16 < m < 81 and -81 < m < -16
ANSWER: A
WORKING:
25 < m^4 + 9 < 90
16 < m^4 < 81
m^4 > 16 so m > 2 and m < -2
m^4 < 81 so m < 3 and m > -3
Combine into two inequalities to get
2 < m < 3 and -3 < m < -2
Question 20 [5 marks]
Solid A, shown below, is a frustum of a cone.
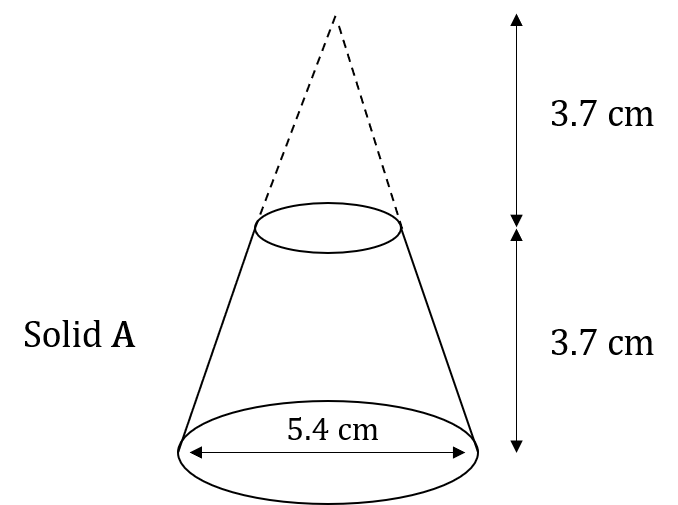
The diagram above shows that the frustum is made by removing a cone with height 3.7 cm from a solid cone with height 7.4 cm and a base diameter of 5.4 cm.
The frustum is joined to a solid cylinder with diameter 5.4 cm and a height of 1.4 cm, to form solid B, as shown below.
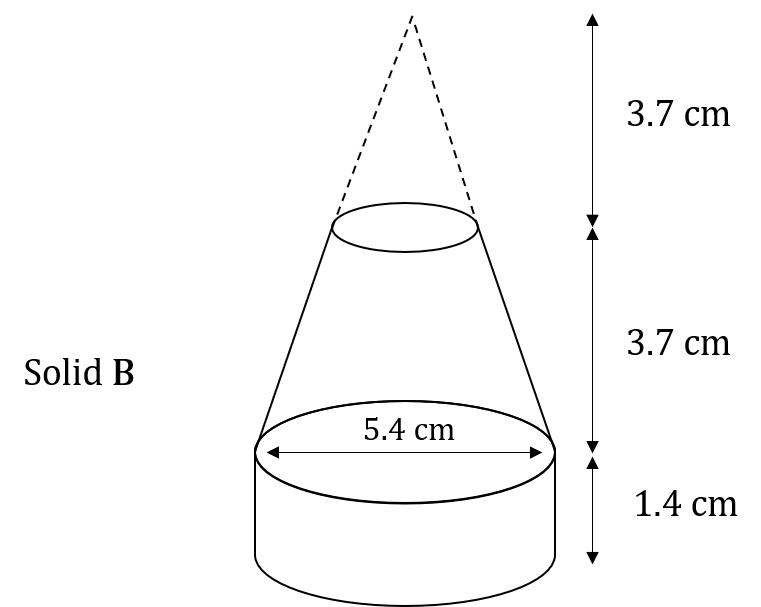
The density of the frustum is 3.3 g/cm^3
The density of the cylinder is 2.8 g/cm^3
Volume of cone = \dfrac{1}{3} \pi r^2 h
Calculate the average density of solid B, correct to 2 decimal places.
Answer type: Multiple choice type 1
A: 3.10 g/cm^3
B: 6.10 g/cm^3
C: 3.05 g/cm^3
D: 3.16 g/cm^3
ANSWER: A
WORKING:
Frustum:
Radius of big cone = 5.4 \div 2 = 2.7 cm
Volume of big cone = \dfrac{1}{3} \times \pi \times 2.7^2 \times 7.4 = 56.4921... cm^3
Radius of small cone = 2.7 \div 2 = 1.35 cm, since the height of the big cone is twice the height of the small cone.
Volume of small cone = \dfrac{1}{3} \times \pi \times 1.35^2 \times 3.7 = 7.0615... cm^3
Volume of frustum = 56.4921... - 7.0615... = 49.4306... cm^3
\text{M} = \text{D} \times \text{V} = 3.3 \times 49.4306... = 163.1209... g
Cylinder:
Radius = 2.7 cm
Volume of cylinder = \pi r^2 h = \pi \times 2.7^2 \times 1.4 = 32.0630... cm^3
\text{M} = \text{D} \times \text{V} = 2.8 \times 32.0630... = 89.7766... g
Total volume = 49.4306... + 32.0630... = 81.4936... cm^3
Total mass = 163.1209... + 89.7766... = 252.8976... g
\text{Average density} = \dfrac{\text{Total mass}}{\text{Total volume}} = \dfrac{252.8976...}{81.4936...} = 3.10 g/cm^3
Question 21 [4 marks]
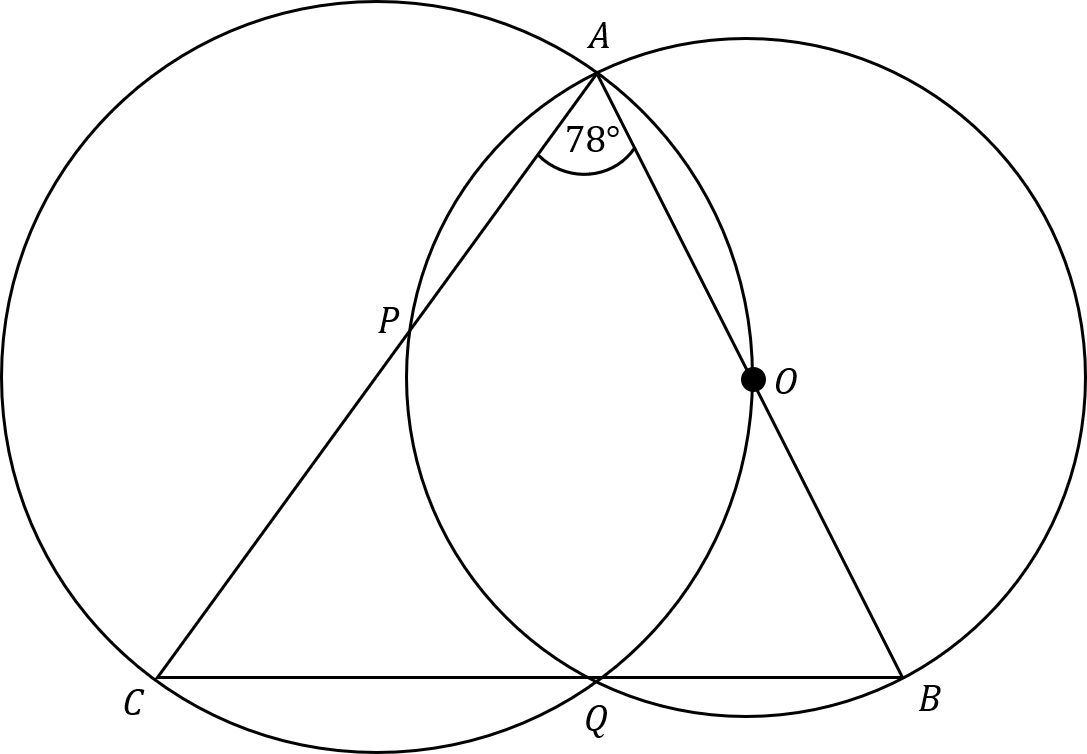
\textit{A.B,Q} and \textit{P} are four points on a circle with centre \textit{O}.
\textit{A,O,Q} and \textit{C} are four points on a different circle.
The two circles intersect at the points \textit{A} and \textit{Q}.
\textit{CPA}, \textit{CQB} and \textit{AOB} are straight lines.
Angle \textit{CAB} = 78 \degree
What is angle \textit{ACB} ?
Answer type: Simple text answer
ANSWER: 24 \degree
WORKING:
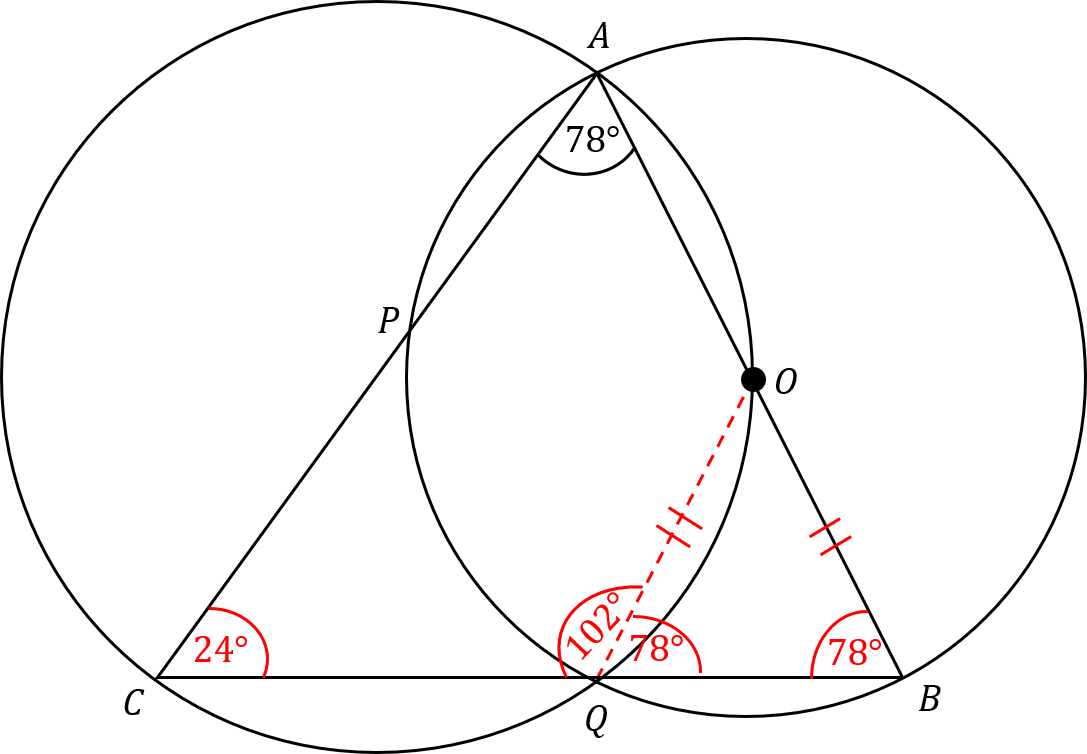
\angle\textit{CQO} = 180 - \angle\textit{CAB} = 180 - 78 = 102 \degree (Cyclic quadrilaterals)
\angle\textit{OQB} = 180 - \angle\textit{CQO} = 180 - 102 = 78 \degree (Angles on a straight line)
OQ = OB, hence \angle\textit{OQB} = \angle\textit{OBQ} = 78 \degree
\angle\textit{ACB} = 180 - \angle\textit{CAB} - \angle\textit{OQB} = 180 - 78 - 78 = 24 \degree (Angles in a triangle)
