NOTE: Q1-6 are the same as Q20-25 on Nov 18 Foundation Paper 3
(DOESN’T NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1(a) [1 mark]
Write 31897 correct to 4 significant figures
Answer type: Simple text answer
ANSWER: 31900
Question 1(b) [2 marks]
What is \dfrac{\sqrt{72 - 4^3}}{2.3^2} correct to 5 decimal places?
Answer type: Simple text answer
ANSWER: 0.53467
WORKING:
\dfrac{\sqrt{72 - 4^3}}{2.3^2} = 0.5346743146 = 0.53467 (5 dp)
Question 2 [3 marks]
Last year David paid £362 for his life insurance.
This year he has to pay £926 for his life insurance.
What is the percentage increase in the cost of his life insurance?
Write your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 155.8\%
WORKING:
Increase =926 - 362 = 564
\% increase = \dfrac{564}{362} \times 100 = 155.801105 = 155.8\% (1 dp)
Question 3
Question 3(a) [2 marks]
Find the values of a, b, c and d to complete this table of values for y=x^2+2x-2

Answer type: Multiple answers type 1
ANSWERS:
a = 1
b = -2
c = -2
d = 6
WORKING:
Substitute the values of x into the equation to find the values of y.

Question 3(b) [2 marks]
Choose the correct plot of y = x^2+2x-2 for values of x between -3 and 2
Answer type: Multiple choice type 1
A:

B:
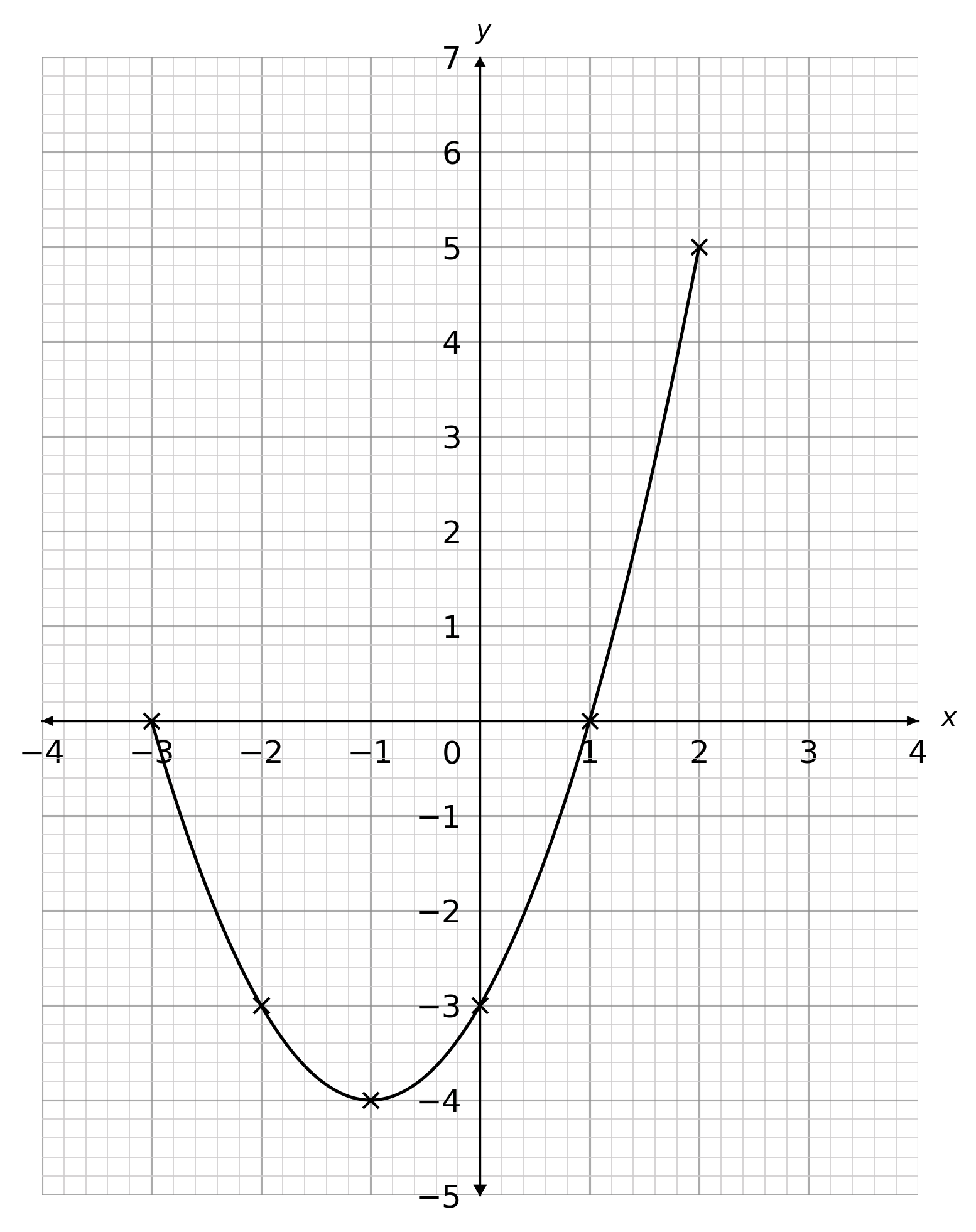
C:
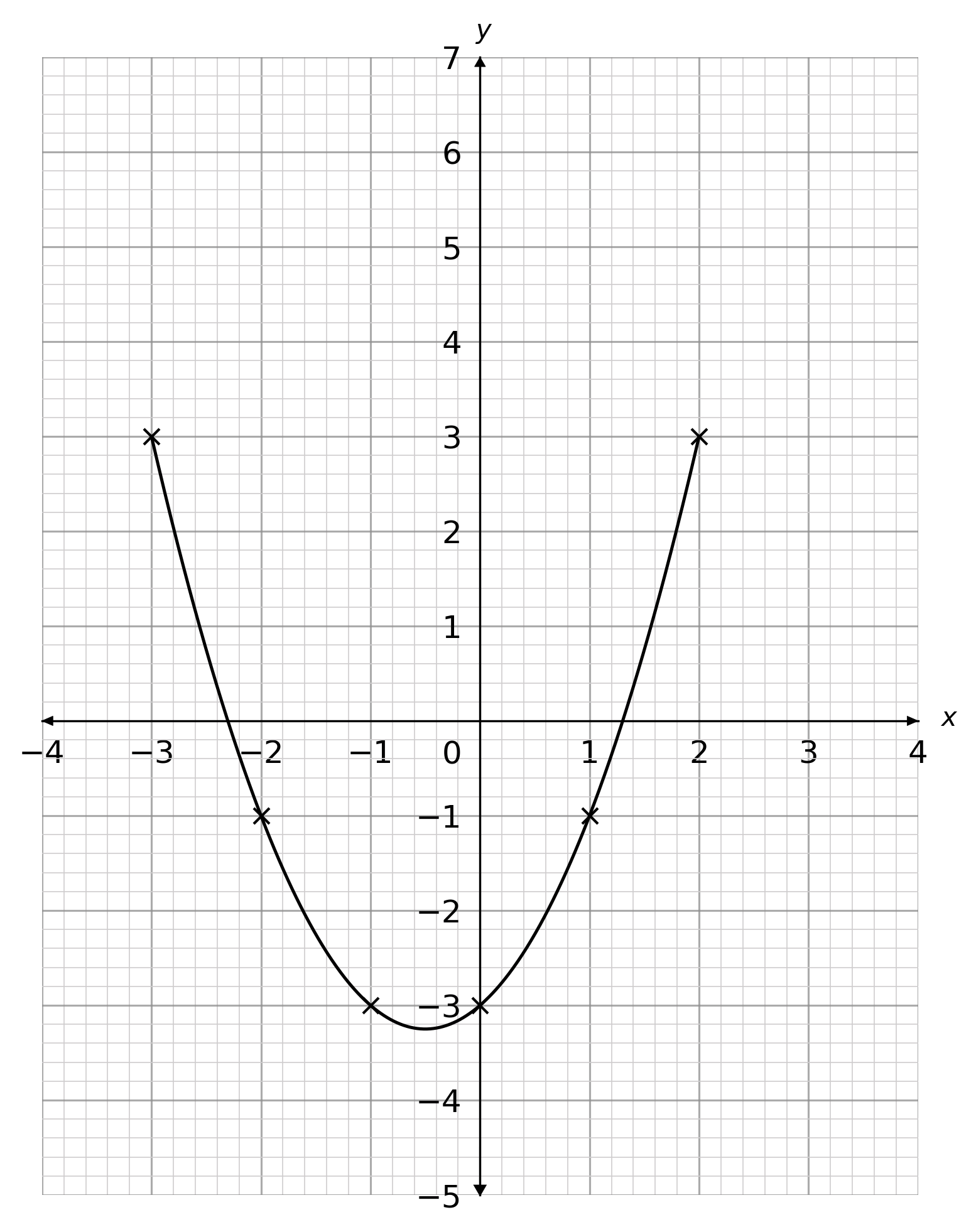
D: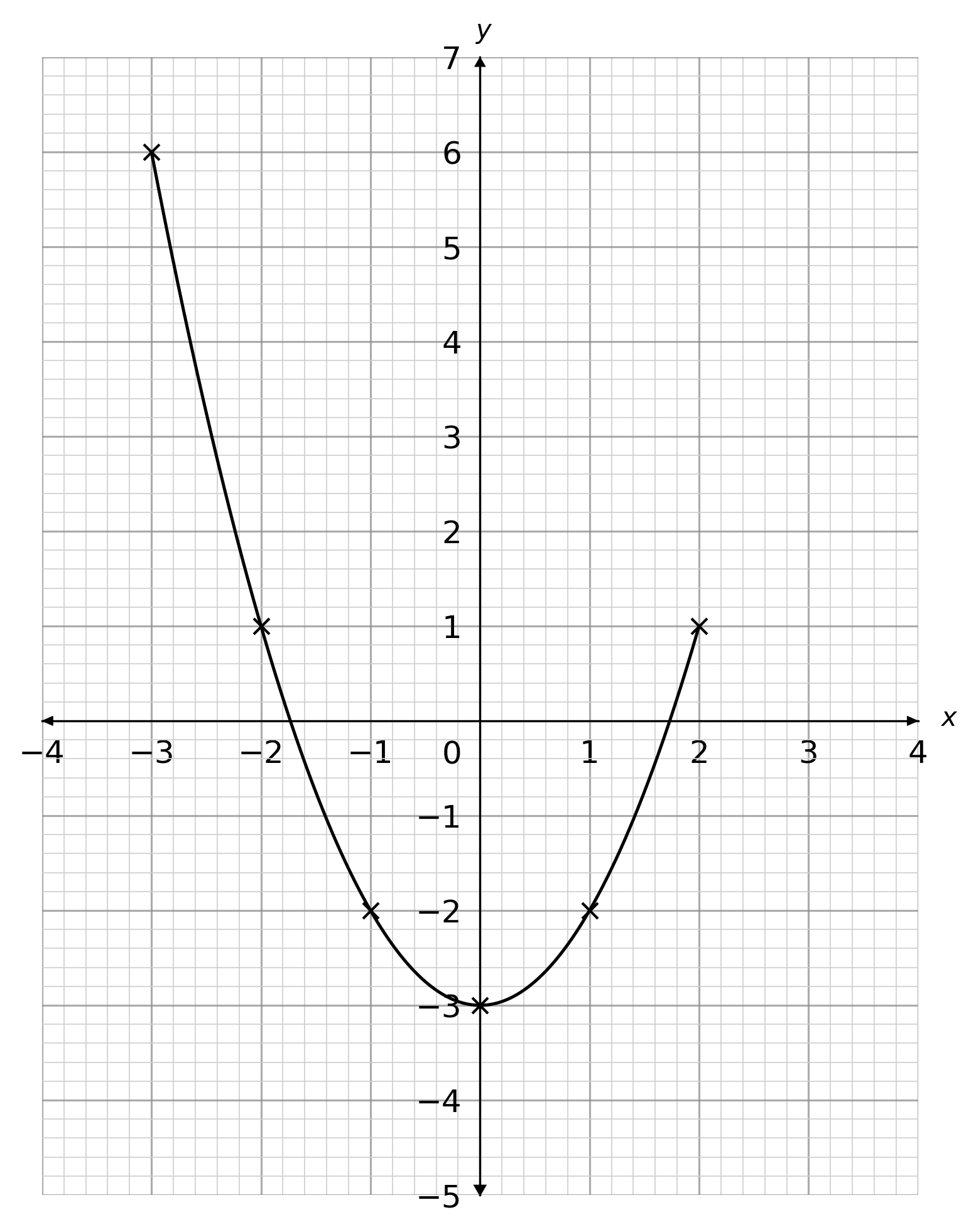
ANSWER: A
Question 3(c) [1 mark]
Use the graph to estimate a solution to x^2 + 2x - 2 = 0
Answer type: Multiple choice type 1
A: x = 0.7 or x = -2.7
B: x = 1.3 or x = -1.3
C: x = 1 or x = 3
D: x = 1.7 or x = -1.7
ANSWER: A
WORKING:
We want to find the x values where the graph crosses the x axis.
This happens at x = 0.7 or x = -2.7
Question 4
Fred asks 30 individuals how many jumpers they bought last year.
The chart below shows information about the number of jumpers bought by each of the 30 individuals.

Question 4(a) [2 marks]
What is the percentage of these individuals who bought less than 10 jumpers?
Answer type: Simple text answer
ANSWER: 40\%
WORKING:
Less than 10 jumpers =12 individuals
\dfrac{12}{30} \times 100 = 40\%
Question 4(b) [4 marks]
What is an estimate for the mean number of jumpers bought?
Answer type: Multiple choice
A: 9.3
B: 3.9
C: 10.4
D: 4.1
ANSWER: A
WORKING:

8 + 4 + 15 + 2 + 1 = 30
16 + 28 + 180 + 34 + 22 = 280
Estimated mean = \dfrac{280}{30} = 9.3
Question 5
Rita is a mountain biker.
She completed a bike race in 4 minutes 34 seconds
The race was 2.2 km in length.
Rita assumes that her average speed is the same for each race.
Question 5(a) [3 marks]
Using this assumption, calculate how long it would take Rita to complete a 4 km race.
Give your answer in minutes and seconds, to the nearest second.
Answer type: Multiple choice type 1
A: 8 minutes 18 seconds
B: 7 minutes 24 seconds
C: 9 minutes 8 seconds
D: 8 minutes 46 seconds
ANSWER: A
WORKING:
2.2 km = 2200 m
4 mins 34 seconds = 240 + 34 = 274 seconds
Average speed = \dfrac{2200}{274} = 8.029... m/s
4 km = 4000 m
Time = \dfrac{4000}{8.029...} = 498.181... seconds
498.181... seconds \div \, 60 = 8.303... minutes = 8 minutes 18 seconds (nearest second)
Question 5(b) [1 mark]
Rita’s average speed actually decreases the further she goes.
How does this affect your answer to part (a)?
Answer type: Multiple choice type 1
A: The race would take more time
B: The race would take less time
C: The race would take the same amount of time
ANSWER: A
Question 6 [4 marks]
ABC is a right-angled triangle.

AB = 6 cm
Angle C = 90 \degree
Size of angle A : Size of angle C = 1:2
Calculate the length of AC
Give your answer to 3 significant figures.
Answer type: Simple text answer
ANSWER: 6.93 cm
WORKING:
\angle A + \angle C = 180 \degree - 90 \degree = 90 \degree
Number of parts in ratio = 1 + 2 = 3
90 \div 3 = 30 \degree
So, \angle A = 30 \degree and \angle C = 2 \times 30 \degree = 60 \degree
Then, SOHCAHTOA to find AC, which we will call x
\sin \theta = \dfrac{\text{O}}{\text{H}}
\sin 60 \degree = \dfrac{6}{x}
x = \dfrac{6}{\sin 60 \degree} = 6.93 cm (3 sf)
Question 7 [2 marks]
The table below gives information about the masses of 100 children.

Choose the correct frequency polygon drawn for this information.
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: A
WORKING:
The points are plotted at midpoints, and then joined up with straight lines.
Question 8 [5 marks]
The diagram below shows a solid chocolate cuboid.
The areas of the three different faces are marked on the diagram.
The lengths, in cm, of the edges of the cuboid are integers.

The chocolate cuboid is melted and made into cubes.
Each of the cubes had sides of length 1.5 cm
What is the greatest number of these cubes that can be made?
Answer type: Simple text answer
ANSWER: 28 cubes
WORKING:
Label the sides of the cuboid as follows:

To find x,y,z we need to consider the common factors of the areas
We get that x = 8, y = 3 and z = 4
Volume of cuboid = 8 \times 3 \times 4 = 96 cm^3
Volume of cube = 1.5 \times 1.5 \times 1.5 = 3.375 cm^3
\dfrac{96}{3.375} = 28.44
therefore the greatest number of cubes is 28
Question 9
Question 9(a)
Expand and simplify (x+1)(2x-1)(x+3)
Answer type: Multiple choice type 1
A: 2x^3 + 7x^2 + 2x - 3
B: 4x + 3
C: 2x^3 + 3x^2 + 2x - 3
D: 2x^3 + 7x^2 - 2x - 3
ANSWER: A
WORKING:
(x+1)(2x-1)(x+3)
=(x+1)(2x^2+6x-x-3)
= (x+1)(2x^2+5x-3)
= (2x^3+ 5x^2 - 3x + 2x^2 + 5x - 3
= 2x^3 + 7x^2 + 2x - 3
Question 9(b) [2 marks]
\dfrac{x^5 \times x^{-2}}{x^n} = x
Find the value of n
Answer type: Simple text answer
ANSWER: 2
WORKING:
Rearrange for x^n
x \times x^n = x^5 \times x^{-2}
x^n = \dfrac{x^5 \times x^{-2}}{x}
x^n = \dfrac{x^{5-2}}{x^1} = \dfrac{x^3}{x^1} = x^{3-1} = x^2
So n = 2
Question 9(c) [3 marks]
Solve 4x^2 - 7x - 5 = 0
Give your answers to 3 significant figures.
Answer type: Multiple answers type 2 (can be either way round)
ANSWERS:
x = -0.545
x = 2.29
WORKING:
a = 4, b = -7, c = -5x = \dfrac{-(-7) \pm \sqrt{(-7)^2 - 4 \times 4 \times (-5)}}{2 \times 4}
x = -0.545 or x = 2.29 (to 3 sf)
Question 10
f(x) = 3 \cos x \degree
Question 10(a) [1 mark]
Calculate f(13)
Give our answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 2.92
WORKING:
f(12) = 3 \cos 12 \degree = 2.92 (2 dp)
Question 10(b)
g(x) = 4x-1
Find gf(25)
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 9.88
WORKING:
gf(x) = 4(3 \cos x \degree) - 1
gf(25) = 4(3 \cos 25 \degree) - 1 = 9.88 (2 dp)
Question 10(c) [1 mark]
h(x) = (x+2)^2
Solve h(x) = 16
Answer type: Multiple choice type 1
A: x = 2 or x = -6
B: x = 2 or x = -2
C: x = 2
D: x = 14
ANSWER: A
WORKING:
(x+2)^2 = 16
x+2 = \pm 4
x = -2 \pm 4
x = 2 or x = -6
Question 11 [2 marks]
The following graph is a sketch of which function, for 0 \leq x \leq 360

Answer type: Multiple choice type 1
A: y = \tan x
B: y = \cos x
C: y = \sin x
D: y = \dfrac{1}{x}
ANSWER: A
Question 12 [4 marks]
Below is a cuboid ABCDEFGH
CH = 3 cm
EF = 8 cm
\angle EFH = 32 \degree
Calculate the length of the diagonal FC
Give your answer to 3 significant figures.
Answer type: Simple text answer
ANSWER: 9.90 cm
WORKING:
\cos \theta = \dfrac{\text{Adjacent}}{\text{Hypotenuse}}
\text{Hypotenuse} = \dfrac{\text{Adjacent}}{\cos \theta}
FH = \dfrac{8}{\cos 32} = 9.4334... cm
FC = \sqrt{3^2 + (9.4334...)^2} = 9.90 cm (3 sf)
Question 13 [2 marks]
The population of a village at the end of the year n is P_n
The population of the village at the end of year 1 is 1200
Given that P_{n+1} = 1.03 \, P_n
calculate the population of the village at the end of year 3, to the nearest whole number.
Answer type: Simple text answer
ANSWER: 1237
WORKING:
P_1 = 1200
P_2 = 1.03 \times 1200 = 1236
p_3 = 1.30 \times 1236 = 1273.08 = 1273 (nearest whole number)
Question 14 [3 marks]
y is inversely proportional to x^2
y = 21 when x = a
Calculate the value of y when x = \dfrac{1}{2} a
Answer type: Simple text answer
ANSWER: 84
WORKING:
y \propto \dfrac{1}{x^2}
So, y = \dfrac{k}{x^2}
k = yx^2 = 21a^2
So, y = \dfrac{21a^2}{x^2}
When x = \dfrac{1}{2} a
y = \dfrac{21a^2}{(\frac{1}{2}a^2)} = \dfrac{21a^2}{\frac{1}{4} a^2} = 84
Question 15 [3 marks]
By use of an algebraic proof, choose the correct statement about the sum of 3 consecutive odd numbers.
Answer type: Multiple choice type 1
A: It is always odd
B: It is always even
C: It is sometimes odd and sometimes even
ANSWER: A
WORKING:
For any 3 consecutive odd numbers: 2n+1, 2n+3 and 2n+5, adding them together gives us,
(2n+1) + (2n+3) + (2n+5) = 6n + 9
We can write this as 6n + 8 + 1
Then, 6n + 8 + 1 = 2(3n+4) + 1
Since 3n+4 is an integer, we can write our expression as 2m + 1 where m = 3n+4
Therefore, the sum of 3 consecutive odd numbers is always odd.
Question 16 [5 marks]
Below is a shape ABCDE

The shape is made from a square ACDE, a triangle AOC and a sector of a circle, centre O and radius 4 cm.
\angle AOC = 126 \degree
Calculate the perimeter of the shape.
Give your answer to 3 significant figures.
Answer type: Simple text answer
ANSWER: 37.7 cm
WORKING:
Diameter = 2 \times 4 = 8 cm
Reflex angle AOC = 360 - 126 = 234 \degree
Arc length ABC = \dfrac{234}{360} \times \pi \times 8 = 16.3362... cm
Triangle AOC is isosceles, so \angle OAC = \angle OCA = (180-126)\div2 = 27 \degree
Using the sine rule, \dfrac{AC}{\sin 126} = \dfrac{4}{\sin 27}
So, AC = \dfrac{4 \sin 126}{\sin 27} = 7.1280... cm
AC is one of the side lengths of the square, so all other sides of the square are 7.1280... cm
Total perimeter = 16.3362 + 3(7.1280...) = 37.7 cm (3 sf)
Question 17
The histogram shows information about the fuel capacity of various vehicles that were surveyed.

Question 17(a) [3 marks]
Using the histogram above and the table below, calculate the number of vehicles that were surveyed.

Answer type: Simple text answer
ANSWER: 346
WORKING:

Total frequency = 24 + 88 + 120 + 74 + 40 = 346
Question 17(b) [2 marks]
Estimate the median fuel capacity.
Give your answer to 2 significant figures.
Answer type: Simple text answer
ANSWER: 60
WORKING:
Median is the \dfrac{346+1}{2} = 173.5 th value, which lies in 50 < f \leq 70
The median is 173.5 - 88 - 24 = 61.5 places into the 120 vehicles from 50 < f \leq 70
\dfrac{61.5}{120} \times 20 = 10.25
Median \approx 50 + 10.25 = 60.25 = 60 (2 sf)
Question 18
A plane from The United Kingdom to Turkey travels a distance of 2520 km in 3 hours 55 minutes.
The distance is measured correct to the nearest 5 km.
The time is measured correct to the nearest minute.
By considering bounds, calculate the average speed of the plane, in km/min, to a suitable degree of accuracy.
Simple text answer
ANSWER: 11 km/min
WORKING:
2517.5 \leq d < 2522.5 234.5 \leq t < 235.5\text{Max average speed} = \dfrac{\text{Max distance}}{\text{Min time}} = \dfrac{2522.5}{234.5} = 10.7569... \text{Min average speed} = \dfrac{\text{Min distance}}{\text{Max time}} = \dfrac{2517.5}{235.5} = 10.6900...
Both the max average speed and min average speed round to 11, so average speed =11 km/min
Question 19 [5 marks]
Solve algebraically the following simultaneous equations
x^2 + 3y^2 = 7
x+y = 2
Answer type: Multiple choice type 1
A: x = \dfrac{5}{2}, y = - \dfrac{1}{2} and x = \dfrac{1}{2}, y = \dfrac{3}{2}
B: x = \dfrac{5}{2}, y = \dfrac{3}{2} and x = \dfrac{1}{2}, y = - \dfrac{1}{2}
C: x = 1, y = 1 and x = \dfrac{1}{2}, y = \dfrac{3}{2}
D: x = \dfrac{5}{2}, y = - \dfrac{1}{2} and x = 2, y = 0
ANSWER: A
WORKING:
From the second equation: x = y - 2
substitute this into the first equation:
(2-y)^2 + 3y^2 = 7
4 - 2y - 2y + y^2 + 3y^2 = 7
4y^2 - 4y + 4 = 7
4y^2 - 4y - 3 = 0
(2y+1)(2y-3)=0
y = - \dfrac{1}{2} and y = \dfrac{3}{2}
Substitute the value of y into the second equation:
x = 2 - \bigg( - \dfrac{1}{2} \bigg) = \dfrac{5}{2}and
x = 2 - \dfrac{3}{2} = \dfrac{1}{2}
x = \dfrac{5}{2}, y = - \dfrac{1}{2} and x = \dfrac{1}{2}, y = \dfrac{3}{2}
Question 20 [2 marks]

Triangle A is transformed by the combined transformation of a rotation of 180 \degree about the point (0,1) followed by a translation with vector \begin{pmatrix} 4 \\ 2 \end{pmatrix}
One point on triangle A is invariant under this combined transformation.
What are the x and y coordinates of this point?
Answer type: Multiple answers type 1
ANSWERS:
x = 2
y = 2
WORKNG:
The rotation of triangle A gives triangle B
The translation of triangle B gives triangle C
Triangle C is the triangle under the combined transformation.
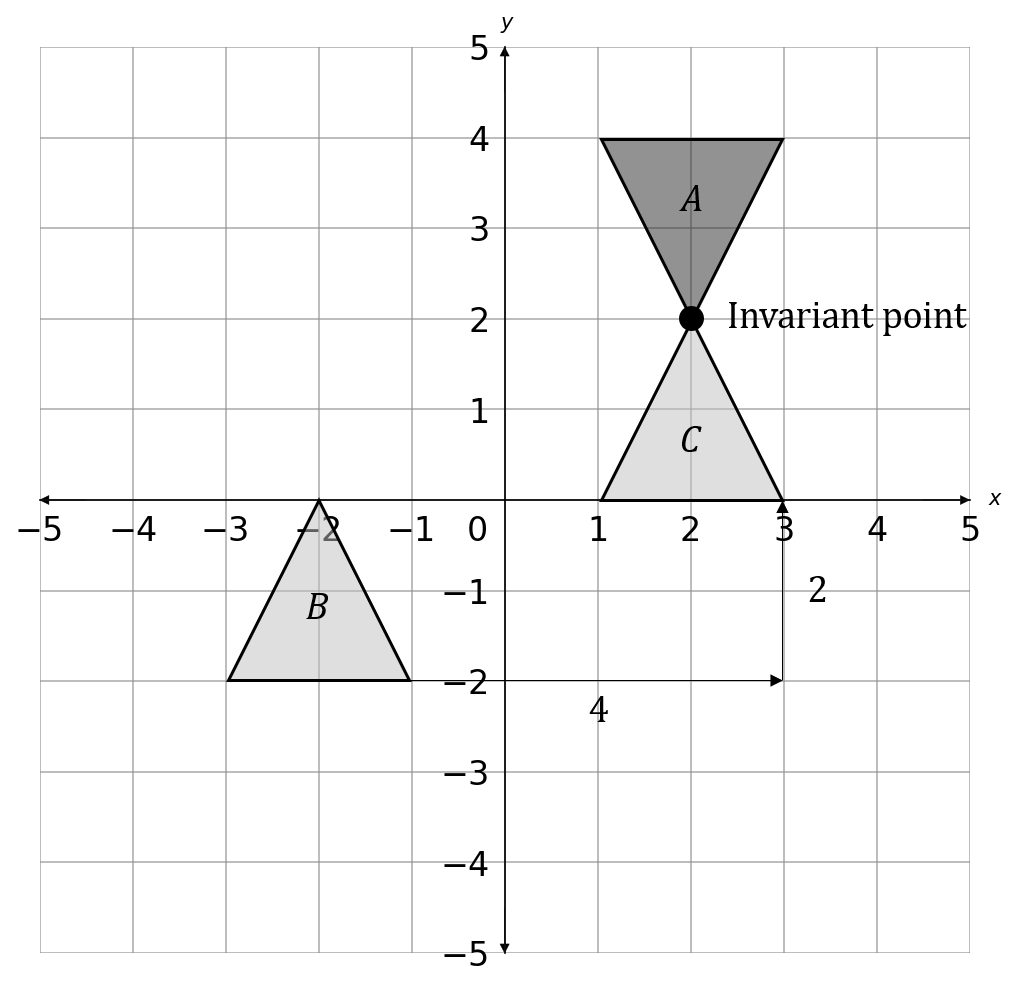
The invariant point is (2,2)
