NOTE: Q20-26 are the same as Q1-7 on Nov 18 Higher Paper 1
(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1 [1 mark]
Write the following numbers in order of size, starting with the largest.
1.21 \,\,\,\,\, 2.11 \,\,\,\,\, 1.12 \,\,\,\,\, 2.12 \,\,\,\,\, 2.21
Answer type: Multiple answers type 1
ANSWERS:
Largest: 2.21
then: 2.12
then: 2.11
then: 1.21
Smallest: 1.12
Question 2 [1 mark]
What is 0.4 as a percentage?
Answer type: Simple text answer
ANSWER: 40 \%
Question 3 [1 mark]
Below is a list of numbers.
2 \,\,\,\,\, 3 \,\,\,\,\, 7 \,\,\,\,\,\, 10 \,\,\,\,\,\, 12 \,\,\,\,\,\, 15 \,\,\,\,\,\, 20
From the list, write down a multiple of 6
Answer type: Simple text answer
ANSWER: 12
Question 4 [1 mark]
What is 839 to the nearest 100?
Answer type: Simple text answer
ANSWER: 800
Question 5
Question 5(a) [1 mark]
Calculate 2 + 4 \times 3
ANSWER:
14
Question 5(b) [1 mark]
Calculate 2^4
i
Answer type: Simple text answer
ANSWER: 16
Question 5(c) [1 mark]
Choose the statement with the correct set of brackets that makes the following statement correct
24 \div 3 + 5 = 3
Answer type: Multiple choice type 1
A: 24 \div (3 + 5) = 3
B: (24 \div 3) + 5 = 3
ANSWER: A
Question 6 [3 marks] – here
Pete has 3 dogs.
Each dog eats \dfrac{1}{6} of a pouch of dog food each day.
Pete buys 3 pouches of dog food.
Has Pete bought enough dog food to feed his 3 dogs for 7 days?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B
WORKING:
3 \times \dfrac{1}{6} = \dfrac{1}{2} pouches per day.
7 \times \dfrac{1}{2} = 3.5 pouches in 7 days.
Pete has only bought 3 pouches, so he has not bought enough dog food.
Question 7 [3 marks]
There are only black, white, grey and blue cars in a car park.
The pictogram shows information about the number of black cars, white cars and grey cars in the car park.

There is a total of 35 cars in the car park.
How many circles will be needed to represent the number of blue cars in the car park?
Answer type: Simple text answer
ANSWER: 2
WORKING:
Number of squares = 6 \frac{3}{4}
Number of cars that are not blue = 4 \times 6\frac{3}{4} = (4 \times 6) + (4 \times \frac{3}{4}) = 24 + 3 = 27
Number of blue cars = 35 - 27 = 8
\dfrac{8}{4} = 2 squares
Question 8

Question 8(a) [1 mark]
What are the x and y coordinates of point A?
Answer type: Multiple answers type 1
ANSWERS:
x = -4
y = 1
Question 8(b) [1 mark]
Which of the following lines represents the line with equation y = -3?

Answer type: Multiple choice type 1
A: Line 1
B: Line 2
C: Line 3
D: Line 4
ANSWER: D
Question 8(c)
Which of the following crosses represents the point (2,-2)?

Write your answer as a CAPITAL LETTER.
Answer type: Simple text answer
ANSWER: D
Question 9 [2 marks]
m = 6 and n = 5
Calculate the value of 4m - 3n
Answer type: Simple text answer
ANSWER: 9
WORKING:
4m - 3n = 4(6) - 3(5) = 24 - 15 = 9
Question 10 [2 marks]
Write down two prime numbers that have a product of 26
Answer type: Multiple answers type 2 (can be either way around)
ANSWERS:
1st number = 2
2nd number = 13
WORKING:
Prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23
There is only one possible solution: 2 \times 13 = 26
Question 11
Here are some fractions:
\dfrac{2}{6} \,\,\,\,\,\,\,\,\,\, \dfrac{11}{33} \,\,\,\,\,\,\,\,\,\, \dfrac{5}{18} \,\,\,\,\,\,\,\,\,\, \dfrac{4}{12} \,\,\,\,\,\,\,\,\,\, \dfrac{8}{24}
Question 11(a) [1 mark]
Which of the fractions above is not equivalent to \dfrac{1}{3}?
Answer type: Fraction
ANSWER: \dfrac{5}{18}
Question 11(b) [2 marks]
Work out \dfrac{1}{8} + \dfrac{3}{4}
Answer type: Fraction
ANSWER: \dfrac{7}{8}
WORKING:
\dfrac{1}{8} + \dfrac{3}{4} = \dfrac{1}{8} + \dfrac{6}{8} = \dfrac{7}{8}
Question 12
Rupert is a taxi driver.
You can use the following graph to find the taxi fare for different distances.

For each taxi fare, there is a fixed charge plus a charge for the distance.
Question 12(a) [1 mark]
How much is the fixed charge?
Answer type: Simple text answer
ANSWER: £4
WORKING:
The fixed charge is the y intercept, which is £4
Question 12(b)
Rupert makes two taxi journeys.
The distance of one journey is 4 miles more than the distance of the other journey.
Calculate the difference between the two taxi fares.
Answer type: Simple text answer
ANSWER: £6
WORKING:
8 miles = £16
4 miles = £10
Difference = £16 - £10 = £6
Question 13 [2 marks]
Miguel, Ron and Sharon each have some sweets.
Miguel has 3 times as many sweets as Sharon.
Ron has half as many sweets as Miguel.
What is the ratio of Miguel’s number of sweets to Ron’s number of sweets to Sharon’s number of sweets, in simplest form?
Answer type: Multiple choice type 1
A: 6:3:2
B: 3:1:2
C: 6:2:1
D: 3:2:1
ANSWER: A
WORKING:
Ratio of the number of sweets Miguel has compared to Sharon =3:1
Ratio of the number of sweets Miguel has compared to Ron =2:1
We can see that Miguel is common in both ratios, so we need to covert both ratios so that the number representing Miguel’s proportion of sweets is the same in both.
Then we can combine the ratios to give us one ratio for Miguel, Ron and Sharon.
3:1=6:2
2:1=6:3
Combining these ratios gives us 6:3:2
Question 14
The diagram below shows a kite ABCD with each of its sides extended.

CB = CD
Find the value of x
Answer type: Simple text answer
ANSWER: 50 \degree
WORKING:
\angle ABC = 80 \degree (vertically opposite angles)
\angle ADC = 80 \degree (opposite angles in a kite are equal)
\angle BCD = 360 - 80 - 80 - 70 = 130 \degree (angles in a quadrilateral)
x = 180 - 130 = 50 \degree (angles on a straight line)
Question 15
Maria is going to use the following instructions to make an alcoholic drink.

Maria has 150 ml of rum and 600 ml of cola.
Question 15(a) [3 marks]
What is the greatest amount of the alcoholic drink she can make?
Answer type: Simple text answer
ANSWER: 500 ml
WORKING:
1 part = 150 \div 3 = 50 ml
Amount of cola = 50 \times 7 = 350 ml
Total amount = 150 + 350 = 500 ml
Question 15(b) [1 mark]
Maria spilt some of her cola and now only has 500 ml left.
What is the greatest amount of the alcoholic drink she can now make?
Answer type: Simple text answer
ANSWER: 500 ml
WORKING:
The maximum amount of cola she can use is 350 ml, so she can still make 500 ml of the alcoholic drink.
Question 16 [1 mark]
Below are two rectangles.

Are the two rectangles similar?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B
WORKING:
15 \div 6 = 2.5
9 \div 3 = 3
The scale factors are not the same, so the rectangles are not similar.
Question 17
100 people are asked if are right-handed or left-handed.
56 of these people are men.
79 of the 100 people are right-handed.
6 women are left-handed.
Question 17(a) [3 marks]
Use this information to find the values of a,b,c,d,e and f from the frequency tree below.

Answer type: Multiple answers type 1
ANSWERS:
a = 56
b = 44
c = 41
d = 15
e = 38
f = 6
WORKING:
Men = 56
Women = 100 - 56 = 44
Left-handed women = 6
Right-handed women = 44 - 6 = 38
Right-handed men = 79 - 38 = 41
Left-handed men = 56 - 41 = 15

Question 17(b) [2 marks]
One of the people who are right-handed is chosen at random.
What is the probability that this person is a man?
Answer type: Fraction
ANSWER: \dfrac{41}{79}
WORKING:
There are 79 people who are right-handed, and 41 of them are men.
Question 18 [4 marks]
Shop A and Shop B sell packets of diced beef.
Each shop has a special offer, seen below.

Which packet of diced beef is better value for money?
Answer type: Multiple choice type 1
A: Shop A
B: Shop B
ANSWER: A
WORKING:
Shop A:
New price = £4 \times 0.9 = £3.60
100 g = £3.60 \div 5 = £0.72
Shop B:
New amount = 500 \times 1.20 = 600 g
100 g = £4.50 \div 600 = £0.75
Shop A is better value for money.
Question 19

Shape A is rotated 90 \degree clockwise about (-1,1) to give shape B.
Which graph shows shape B in the correct position?
Answer type: Multiple choice type 1
A:
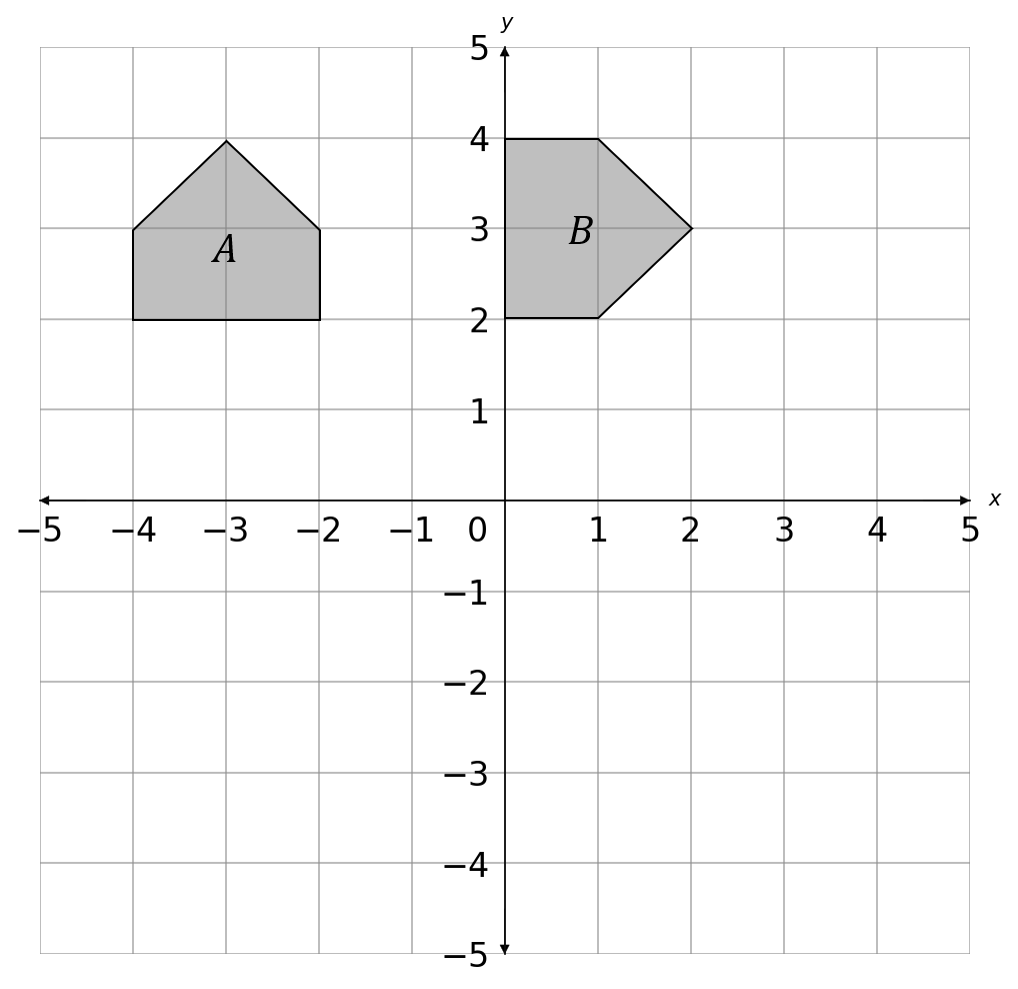
B:
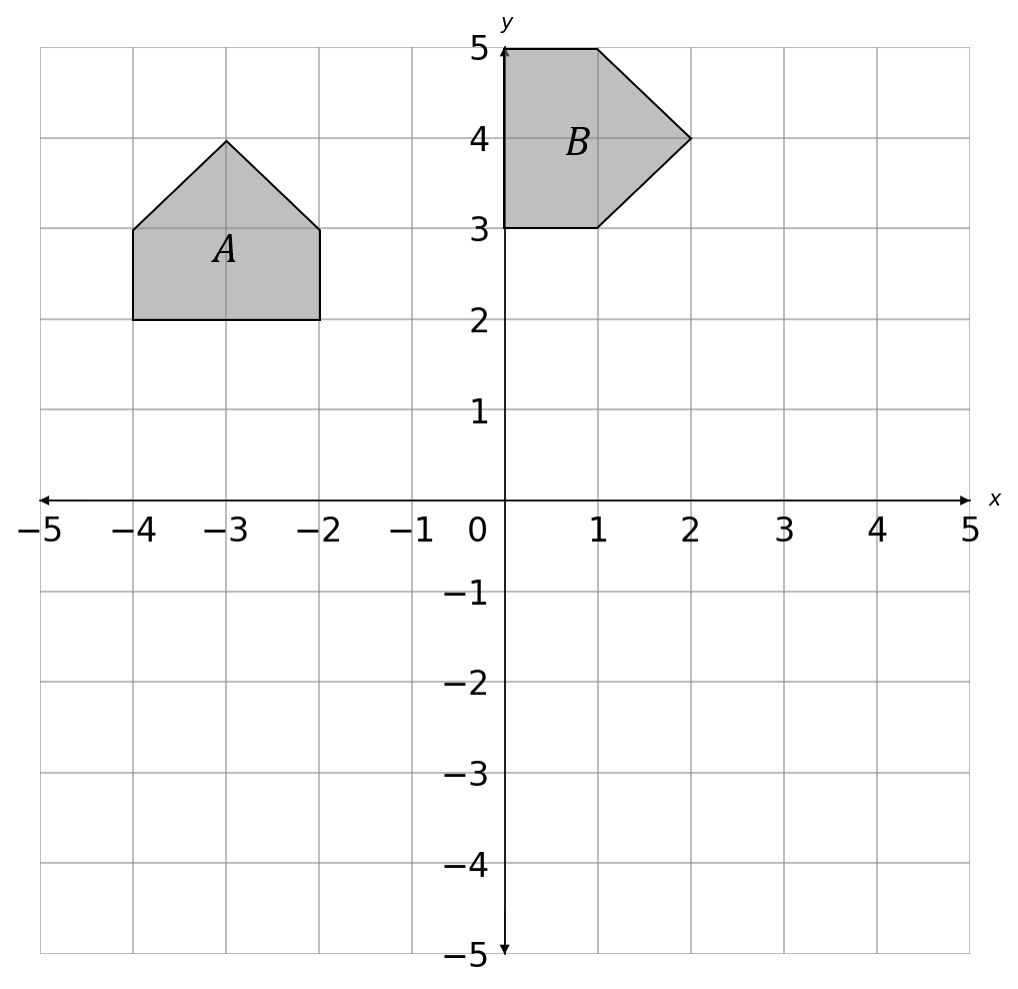
C:

D:

ANSWER: A
WORKING:

Question 20 [2 marks]
Work out the value of \dfrac{2^5 \times 2^{-3}}{2^4}
Answer type: Fraction
ANSWER: \dfrac{1}{4}
WORKING:
\dfrac{2^5 \times 2^{-3}}{2^4} = \dfrac{2^2}{2^4} = \dfrac{4}{16} = \dfrac{1}{4}
Question 21
a^2 = 2b^2 - cdb = 3 \,\,\,\, \,\,\,c = 2 \,\,\,\,\,\,\,d = 1
Question 21(a) [2 marks]
Work out the positive value of a
Answer type: Simple text answer
ANSWER: 4
WORKING:
a^2 = 2(3)^2 - (2)(1) = 18 - 2 = 16
a = \sqrt{16} = \pm 4
So the positive value of a = 4
Question 21(b) [2 marks]
Make c the subject of a^2 = 2b^2 - cd
Answer type: Multiple choice
A: c = \dfrac{2b^2 - a^2}{d}
B: c = \dfrac{a^2 - 2b^2}{d}
C: c = \dfrac{2b^2 - d}{a^2}
D: c = \dfrac{d}{2b^2 - a^2}
ANSWER: A
WORKING:
a^2 + cd = 2b^2
cd = 2b^2 - a^2
c = \dfrac{2b^2 - a^2}{d}
Question 22 [5 marks]
A bonus of £4500 is shared by 12 people who work for a company.
30\% of the bonus is shared equally between 3 managers.
The rest of the bonus is shared equally between 9 salesmen.
If the bonus was shared equally between all 12 people, what would be the percentage increase of 1 salesman’s bonus?
Give your answer to the nearest whole number.
Answer type: Simple text answer
ANSWER: 7 \%
ANSWER: A
WORKING:
4500 \times 0.7 = 3150 shared between salesmen
£3150 \div 9 = £350 for each salesman
If all 12 people shared the bonus equally, they would each get £4500 \div £12 = £375 bonus
The difference is £375 - £350 = £25
\dfrac{25}{350} = 0.07 (1 dp) using the bus stop method
Percentage increase = 0.07 \times 100 = 7 \% (nearest whole number)
Question 23
It would take 150 minutes to fill a water tank using water from 6 taps.
Question 23(a) [2 marks]
How many minutes would it take to fill the tank if only 4 of the taps are used?
Answer type: Simple text answer
ANSWER: 225 minutes
WORKING:
150 minutes for 6 taps
150 \times 6 = 900 minutes for 1 tap
\dfrac{900}{4} = 225 minutes for 4 taps
Question 23(b) [1 mark]
Which of the following assumptions is correct based on your working out to part (a)?
Answer type: Multiple choice
A: Each taps fills at the same rate
B: Each tap fills at a different rate
C: 4 taps will fill the pool quicker than 6 taps
D: 1 tap can fill the tank in 25 minutes
ANSWER: A
Question 24
A train travels at a speed of 98 miles per hour.
Question 24(a) [3 marks]
What is an estimate for the number of seconds the train would take to travel 1 mile?
Answer type: Multiple choice
A: 36 seconds
B: 26 seconds
C: 18 seconds
D: 58 seconds
ANSWER: A
WORKING:
\text{Time in hours} = \dfrac{\text{distance}}{\text{speed}} = \dfrac{1}{98} \approx \dfrac{1}{100}
\text{Time in seconds} = \dfrac{1}{100} \times 60 \times 60 = 36 \, \, \text{seconds}
Question 24(b) [1 mark]
Is your answer to part (a) an underestimate or overestimate?
Answer type: Multiple choice
A: Underestimate
B: Overestimate
ANSWER: A
WORKING:
Underestimate as the speed is rounded up.
Question 25
For the simultaneous equations
6x - 17y = 30
x - 4y = 12
find the values of x and y?
Answer type: Multiple answer
ANSWER:
x = -12
y = -6
WORKING:
6x - 17y = 30 \,\,\, (1)
6x - 24y = 72 \,\,\, (2)
Subtract (2) from (1) to get -7y = 42 so y = -6
Substitute y=-6 into (1) and solve
6x - 17(-6) = 30
6x + 102 = 30
6x = -72
x = -12
So, x = -12 and y = -6
Question 26 [4 marks]
The diagram shows a square \textit{ABCD} with sides of length 8 cm.
It also shows a semicircle and a quadrant.

\textit{BC} is the diameter of the semicircle.
\textit{AE} is the radius of the quadrant.
What is the area of the shaded region?
Answer type: Multiple choice
A: 64 - 9\pi cm^2
B: 8 - 9\pi cm^2
C: 64 + 9\pi cm^2
D: 8 + 9\pi cm^2
ANSWER: A
WORKING:
Area of the semicircle:
\dfrac{1}{2} \times \pi \times r^2 = \dfrac{1}{2} \times \pi \times 4^2 = \dfrac{1}{2} \times \pi \times 16 = 8 \pi cm^2
Area of the quadrant:
\dfrac{1}{4} \times \pi \times r^2 = \dfrac{1}{4} \times \pi \times 2^2 = \dfrac{1}{4} \times \pi \times 4 = \pi cm^2
Area of the square \textit{ABCD}\,:
8 \times 8 = 64 cm^2
Area of shaded region = 64 - 8\pi - \pi = 64 - 9\pi cm^2
Question 27
Sunita is planning on sitting her driving theory exam and her driving practical exam.
The probability of her passing her theory exam is 0.65
The probability of her failing her practical exam is 0.4
Question 27(a) [2 marks]
Find the values of a,b,c and d from the probability tree diagram below.

Answer type: Multiple answers type 1
ANSWERS:
a = 0.35
b = 0.6
c = 0.6
d = 0.4
WORKING:
a = 1 - 0.65 = 0.35
b = 1 - 0.4 = 0.6
c = 0.6
d = 0.4

Question 27(b) [2 marks]
What is the probability that Sunita fails both exams?
Answer type: Simple text answer
ANSWER: 0.14
WORKING:
0.35 \times 0.4 = 0.14
Question 28 [3 marks]
The size of each exterior angle of a regular polygon is \dfrac{1}{4} the size of each interior angle.
How many sides does the polygon have?
Answer type: Simple text answer
ANSWER: 10 sides
WORKING:
x + 4x = 180
5x = 180
x = 180 \div 5 = 36
\text{Exterior angle} = \dfrac{360}{n}
n = \dfrac{360}{\text{Exterior angle}} = \dfrac{360}{36} = 10
So, the polygon has 10 sides
