NOTE: Q20-25 are the same as Q1-6 on Nov 18 Higher Paper 2
(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1 [1 mark]
What is the value of 3 in the number \,\, 389.1
Answer type: Simple text answer
ANSWER: 300
Question 2 [1 mark]
Write down a square number that is also an even number, and is less than 10
Answer type: Simple text answer
ANSWER: 4
Question 3
Question 3(a) [1 mark]
Convert 2260 ml into litres
Give your answer to 2 decimal places
Answer type: Simple text answer
ANSWER: 2.26 litres
WORKING:
2260 ml \div \, 1000 = 2.26 litres
Question 3(b) [1 mark]
Convert 3.4 m into cm
Answer type: Simple text answer
ANSWER: 340 cm
WORKING:
3.4 m \times \, 100 = 340 cm
Question 4 [1 mark]
Work out the cube root of 27
Answer type: Simple text answer
ANSWER: 3
WORKING:
3 \times 3 \times 3 = 27
Question 5 [1 mark]
Write 0.42 as a fraction in simplest form.
Answer type: Fraction
ANSWER: \dfrac{21}{50}
WORKING:
0.42 = \dfrac{42}{100} = \dfrac{21}{50}
Question 6 [2 marks]
Below are four fractions.
\dfrac{1}{4} \,\,\,\,\, \dfrac{4}{15} \,\,\,\,\, \dfrac{6}{25} \,\,\,\,\, \dfrac{2}{7}
Order the fractions from largest to smallest.
Answer type: Multiple choice type 1
A: \dfrac{2}{7} \,\,\,\,\, \dfrac{4}{15} \,\,\,\,\, \dfrac{1}{4} \,\,\,\,\, \dfrac{6}{25}
B: \dfrac{2}{7} \,\,\,\,\, \dfrac{4}{15} \,\,\,\,\, \dfrac{6}{25} \,\,\,\,\, \dfrac{1}{4}
C: \dfrac{6}{25} \,\,\,\,\, \dfrac{1}{4} \,\,\,\,\, \dfrac{4}{15} \,\,\,\,\, \dfrac{2}{7}
D: \dfrac{6}{25} \,\,\,\,\, \dfrac{4}{15} \,\,\,\,\, \dfrac{1}{4} \,\,\,\,\, \dfrac{2}{7}
ANSWER: A
WORKING:
Convert all fractions into decimals
1 \div 4 = 0.25
4 \div 15 = 0.266...
6 \div 25 = 0.24
2 \div 7 = 0.285...
Then we can order them from largest to smallest
0.285... \,\,\,\,\, 0.266... \,\,\,\,\, 0.25 \,\,\,\,\, 0.24
Then we replace the decimals back with the fractions
\dfrac{2}{7} \,\,\,\,\, \dfrac{4}{15} \,\,\,\,\, \dfrac{1}{4} \,\,\,\,\, \dfrac{6}{25}
Question 7
Question 7(a) [1 mark]
Simplify 4q - q + 2q - 3q
Answer type: Multiple choice type 1
A: 2q
B: q
C: 3q
D: 4q
ANSWER: A
WORKING:
4q - q + 2q - 3q = 2q
Question 7(b) [1 mark]
Simplify 3 \times t \times r \times 5
Answer type: Multiple choice type 1
A: 15rt
B: 3t + 5r
C: 5rt
D: 3r + 5t
ANSWER: A
WORKING:
3 \times t \times r \times 5 = 15rt
Question 8 [2 marks]
A map has a scale of 1 cm to 120 km
On the map, the distance between Paris and London is 2.9 cm
What is the real distance, in km, between Paris and London?
Simple text answer
ANSWER: 348 km
WORKING:
2.9 \times 120 = 348 km
Question 9
Question 9(a) [2 marks]
The nth term of a sequence is 2n+5
Is 32 a term in the sequence?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B
WORKING:
2n+5 = 32
2n = 27
n = 13.5, so 32 is not a term in the sequence
Question 9(b) [2 marks]
Here are the first four terms in a different sequence
2 \,\,\,\,\,\,\,\,\,\, 9 \,\,\,\,\,\,\,\,\,\, 16 \,\,\,\,\,\,\,\,\,\, 23
Calculate the 7th term in the sequence.
Answer type: Simple text answer
ANSWER: 44
WORKING:
Each number increases by 7 each time, so we can write out the next three terms
2 \,\,\,\,\, 9 \,\,\,\,\, 16 \,\,\,\,\,23\,\,\,\,\,30\,\,\,\,\,37\,\,\,\,\,44
So, the 7th term is 44
Question 10
Below is a function machine.

Question 10(a) [1 mark]
Calculate the output when the input is 4
Answer type: Simple text answer
ANSWER: 28
WORKING:
4 + 3 = 7
7 \times 4 = 28
Question 10(b) [2 marks]
Calculate the input when the output is 56
Answer type: Simple text answer
ANSWER: 11
WORKING:
56 \div 4 = 14
14 - 3 = 11
Question 11 [3 marks]
Jay’s pocket money per month is 25\% of £120
Betty’s pocket money per month is £32
Work out the difference between the pocket money Jay gets and the pocket money Betty gets.
Answer type: Simple text answer
ANSWER: £2
WORKING:
Jay’s pocket money = 0.25 \times £120 = £30
Betty’s pocket money = £32
Difference = £32 - £30 = £2
Question 12 [2 marks]
There are 89 balls in a bag.
36 of the balls are pink.
The rest of the counters are orange.
One of the balls is taken at random.
What is the probability that the ball is orange?
Give your answer as a fraction in simplest form.
Answer type: Fraction
ANSWER: \dfrac{53}{89}
WORKING:
89-36=53 orange balls out of a possible 89
Question 13
A square has a perimeter of 24 cm
Question 13(a) [2 marks]
Calculate the area of the square.
Answer type: Simple text answer
ANSWER: 36 cm^2
WORKING:
24 \div 4 = 6 cm each side
Area = 6 \times 6 = 36 cm^2
Question 13(b) [3 marks]
The diagram below shows a right-angled triangle and a trapezium.

The area of the trapezium is 3 times the area of the triangle.
The perpendicular height of the trapezium is h cm.
Calculate the value of h.
Answer type: Simple text answer
ANSWER: h = 6 cm
WORKING:
Area of triangle = \dfrac{1}{2} \times 7 \times 8 = 28 cm^2
Area of trapezium = 3 \times 28 = 84 cm^2
\dfrac{1}{2}(16+12)h=84
14h=84
h = 6 cm
Question 14
Charlie spins a fair 8 sided spinner, numbered 1 to 8
Question 14(a)
What is the probability of landing on an even number?
Answer type: Fraction
ANSWER: \dfrac{1}{2}
WORKING:
The even numbers are 2,4,6,8 so there are 4 even numbers out of 8
Probability of landing on an even number = \dfrac{4}{8} = \dfrac{1}{2}
Question 14(b) [1 mark]
Jessie throws the spinner twice.
What is the probability of getting a number 8 on both spins?
Answer type: Fraction
ANSWER: \dfrac{1}{64}
WORKING:
Probability of landing on number 8 = \dfrac{1}{8}
Probability of landing on 8 for both spins = \dfrac{1}{8} \times \dfrac{1}{8} = \dfrac{1}{64}
Question 14(c) [2 marks]
Ian spins the spinner once.
He also throws a coin to get heads or tails.
How many possible outcomes can Ian get?
Answer type: Simple text answer
ANSWER: 16
WORKING:
Possible outcomes:
H1, H2, H3, H4, H5, H6, H7, H8
T1, T2, T3, T4, T5, T6, T7, T8
So, there are 16 possible outcomes Ian can get.
Question 15 [3 marks]
Eden invests £500 for 4 years into a savings account.
By the end of the 4 years he has received a total of £60 simple interest.
Calculate the annual rate of simple interest.
Answer type: Simple text answer
ANSWER: 3 %
WORKING:
£60 \div 4 = £15 interest saved each year
\dfrac{15}{500} \times 100 = 3 \%
Question 16 [2 marks]

What is the single transformation that maps shape A onto shape B?
Answer type: Multiple choice type 1
A: Reflection in the y-axis
B: Reflection in the x-axis
C: Rotation 180 \degree about the origin
D: Rotation 90 \degree anticlockwise about the origin
ANSWER: A
Question 17 [3 marks]
Jean is going to make some cornflake nest buns.
She needs
100 g of butter
250 g of milk chocolate
300 g of cornflakes
In her kitchen, she already has 200 g of butter and 100 g of cornflakes.
The ingredients are sold in the following quantities at the supermarket.

How much does Jean need to spend at the supermarket in order to make the cornflake nest buns?
Answer type: Simple text answer
ANSWER: £5.05
WORKING:
300 - 100 = 200 g of cornflakes needed
\dfrac{200}{500} = 0.4, so she needs 1 box of cornflakes, costing £1.75
200 - 100 = 100 g of butter spare, so she doesn’t need to buy any butter
She needs to buy 250 g of chocolate, since there is none in her kitchen.
\dfrac{250}{100} = 2.5, so she needs to buy 3 bars of chocolate, costing 3 \times £1.10 = £3.30
Total cost = £1.75 + £3.30 = £5.05
Question 18
Afzal wants to increase 250 by 6\%
Question 18(a) [1 mark]
What number should he multiply 250 by to get this increase?
Answer type: Simple text answer
ANSWER: 1.06
Question 18(b) [1 mark]
Samiha wants to decrease 250 by 6 \%
What will be the answer if she performs this calculation?
Answer type: Simple text answer
ANSWER: 235
WORKING:
250 \times 0.94 = 235
Question 19
Question 19(a) [2 marks]
Solve 4(x-2) = 20
Answer type: Simple text answer
ANSWER: x = 7
WORKING:
4(x-2) = 20
4x - 8 = 20
4x = 28
x = 7
Question 19(b) [2 marks]
Choose the correct factorisation of 15a^2 - 25a
Answer type: Multiple choice type 1
A: 5a(3a-5)
B: 3a(5a-3)
C: 5a(5a-3)
D: 5a(5-3a)
ANSWER: A
WORKING:
15a^2 - 25a = 5(3a^2 - 5a) = 5a(3a-5)
Question 20
\sigma = \{odd numbers between 10 and 40\}
\textit{A} = \{11,13,27,39\}
\textit{B} = \{15,19,21,27,35\}
\textit{C} = \{13,19,27,31\}
Question 20(a) [4 marks]
Which of the following Venn diagrams is correct?
Answer type: Multiple choice
A:

B:
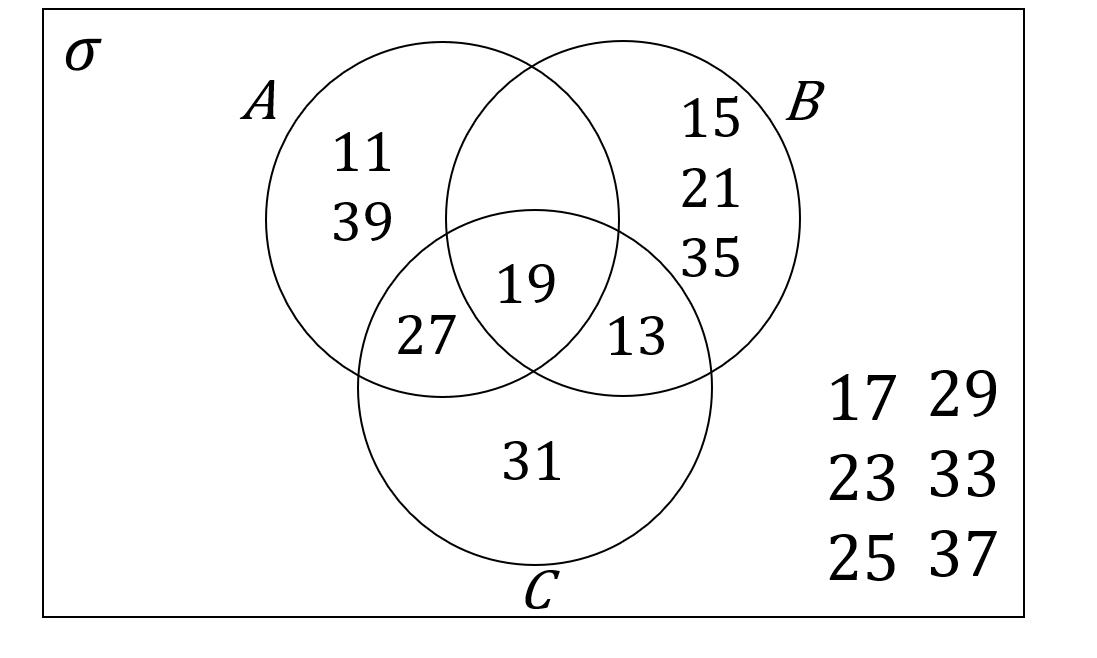
C:

D:

ANSWER: A
Question 20(b) [2 marks]
A number is chosen at random from \sigma.
Find the probability that the number is a member of A \cup C
Answer type: Fraction
ANSWER: \dfrac{6}{15}
WORKING:
A \cup C = A or C
The numbers that satisfy A or C are 11,13,19,27,31,39
There are a total of 15 numbers in \sigma
Probability =\dfrac{6}{15}
Question 21 [2 marks]
Michael has information about how many hours 10 students revised for their maths exam and the results they achieved.
He is asked to draw a scatter graph and a line of best fit for this information.
Here is his answer.

Michael has plotted the points accurately.
What is wrong with his answer?
Answer type: Multiple choice
A: The line of best fit is inaccurate.
B: The labels on the y axis are not linear.
C: There is no correlation between the time spent revising and the result achieved.
D: The time should start at 140 hours.
ANSWER: A
Question 22 [4 marks]
\textit{BEG} is a triangle.
\textit{ABC} and \textit{DEF} are parallel lines.

What is the size of angle x?
Answer type: Simple text answer
ANSWER: 52 \degree
WORKING:

\angle\textit{BEG} = 180 - \angle\textit{DEB} - \angle\textit{GEF} = 180 - 120 - 110 = 50 \degree
\angle\textit{ABE} + \angle\textit{DEB} = 180 \degree so = \angle\textit{ABE} = 180 - 120 = 60 \degree
\angle\textit{EBG} = 180 -\angle\textit{ABE} - \angle\textit{CBG} = 180 - 60 - 42 = 78 \degree
\angle\textit{BGE} = 180 - \angle\textit{BEG} - \angle\textit{ABE} = 180 - 50 - 78 =52 \degree
So, x = 52 \degree
Question 23
Southern Bank has two types of account.
Both accounts pay compound interest.
Savings account: Interest 3\% per annum
Shares account: Interest 4.5\% per annum
Amy invests £3500 in the savings account.
Barney invests £2100 in the shares account.
Question 23(a) [4 marks]
How much more interest will Amy get than Barney by the end of 3 years?
Answer type: Multiple choice
A: £28.05
B: £82.50
C: £25.08
D: £52.80
ANSWER: A
WORKING:
Amy:
3500 \times 1.03^3 = £3824.54 (nearest penny)
Interest = £3824.54 - £3500 = £324.54
Barney:
2100 \times 1.045^3 = £2396.49 (nearest penny)
Interest = £2396.49 - £2100 = £296.49
Difference = £324.54 - £296.49 = £28.05
Question 23(b) [1 mark]
In the 3rd year the rate of interest for the savings account is changed to 3.5\% per annum.
Would Amy still get the most interest by the end of 3 years?
Answer type: Multiple choice
A: Yes
B: No
ANSWER: A
WORKING:
Amy already gets the most interest and so increasing her interest to 3.5\% will only make her get even more.
Question 24 [5 marks]
The diagram shows a floor in the shape of a trapezium.

James is going to varnish the floor.
Each 8 litre tin of varnish costs £21.49
1 litre of varnish covers an area of 5 m^2
James has £130 to spend on varnish.
How much more money would James need to buy all the varnish required to varnish the whole floor?
Answer type: Simple text answer
ANSWER: £20.43
WORKING:
Area of the trapezium =\dfrac{1}{2}(18+25) \times 12 = 258 m^2
As 1 litre of varnish is 5 m^2, 1 tin of varnish covers an area of 8 \times 5 = 40 m^2
\dfrac{258}{40} = 6.45, so James needs 7 tins
Total cost = 7 \times 21.49 = £150.43
Money needed = 150.43 - 130 = £20.43
Question 25 [3 marks]
\textit{A} is the point with coordinates (4, 19)
\textit{B} is the point with coordinates (7,z)
The gradient of the line \textit{AB} is 5
What is the value of z?
Answer type: Simple text value
ANSWER: 34
WORKING:
Gradient of \textit{AB} = \dfrac{\text{Change in } y}{\text{Change in } x} = \dfrac{z - 19}{7 - 4} = \dfrac{z - 19}{3} = 5
Rearrange to get
z - 19 = 15
z = 34
Question 26
Question 26(a) [2 marks]
Expand and simplify (3x-5)(4x+2)
Answer type: Multiple choice type 1
A: 12x^2 - 14x - 10
B: 12x^2 - 14x + 10
C: 12x^2 + 14x - 10
D: 12x^2 - 24x - 10
ANSWER: A
WORKING:
(3x-5)(4x+2)
= 12x^2 + 6x - 20x - 10
= 12x^2 - 14x - 10
Question 26(b) [2 marks]
Choose the correct factorisation of 2x^2 - 5x + 3
Multiple choice type 1
A: (2x-3)(x-1)
B: (2x-1)(x-3)
C: (2x+3)(x+1)
D: (2x-3)(x+1)
ANSWER: A
Question 27
Question 27(a) [1 mark]
What is 0.000326 in standard form?
Answer type: Multiple choice type 1
A: 3.26 \times 10^{-4}
B: 3.26 \times 10^{-3}
C: 3.26 \times 10^{4}
D: 3.26 \times 10^{3}
ANSWER: A
WORKING:
The decimal point moves 4 places to the right, so the power is -4
Question 27(b) [1 mark]
What is 6.891 \times 10^5 as an ordinary number?
Answer type: Simple text answer
ANSWER: 689100
WORKING:
The decimal point moves 5 places to the right, and we fill the rest in with zeros.
Question 27(c) [2 marks]
Calculate \dfrac{3.4 \times 10^6 \times 7.9 \times 10^{-3}}{4 \times 10^4}
Write your answer as an ordinary number.
Answer type: Simple text answer
ANSWER: 0.6715
WORKING:
\dfrac{3.4 \times 10^6 \times 7.9 \times 10^{-3}}{4 \times 10^4}
= \dfrac{26.86 \times 10^3}{4 \times 10^4}
= \dfrac{26.86}{4 \times 10^1}
= \dfrac{26.86}{40}
= 0.6715
