NOTE: Q1-7 same as Q23-29 on foundation paper
Question 1
Write 96 as a product of its prime factors.
ANSWER: Multiple Choice
A: 2^5\times 3
B: 2^4\times 3
C: 3^5\times 2
D: 3^4\times 2
Answer: A
Workings:

Marks = 2
Question 2
Alice is 4 years older than Bob.
Claire is twice as old as Alice.
The sum of their three ages is 48
Find the ratio of Bob’s age to Alice’s age to Claire’s age.
Answer: Multiple Choice
A: 9:13:26
B: 8:16:32
C: 12:18:36
D: 7:14:28
Answer: A
Workings:
Represent Alice as A, Bob as B and Claire as C.
A - 4 = B
C = 2A
A + B + C = 48
Substitute the first two equations in to the third to get it in terms of A.
2A + A - 4 + A = 48
4A - 4 = 48
A = \dfrac{52}{4} = 13
The value for A can then be substituted into the first two equations to find B and C.
A - 4 = 13 - 4 = 9 = B
2A = 2\times 13 = 26 = C
Therefore the ratio of Bob’s age to Alice’s age to Claire’s age can be written as: \,\,\,9:13:26
Marks = 4
Question 3

ABCD is a parallelogram.
CBF is a straight line.
DEF is a straight line that intersects with AB at point E.
Angle BEF = 27\degree
Angle ABC = 82\degree
Calculate the angle ADE.
ANSWER: Simple text answer
Answer: 55 \degree
Workings:
Adjacent angles in a Parallelogram add up to 180, so DAE = 180\degree - ABC = 180\degree - 82 = 98\degree
Angles AED and BEF are vertically opposite and therefore identical, so AED = BEF = 27\degree
Angles in a triangle add up to 180\degree, so 98\degree+27\degree + ADE = 180\degree
ADE = 180\degree - 98\degree - 27\degree = 55\degree
Marks = 4
Question 4
The diagram shows a circular badge containing another circle within.
Both circles have the same centre, O.
The inner circle is split into two sections horizontally along its centre.

Calculate the shaded area of the badge in terms of \pi
ANSWER: Multiple Choice
A: 32\pi cm^2
B: 24\pi cm^2
C: 28\pi cm^2
D: 28\pi cm^2
Answer: A
Workings:
The diameter of the larger circle is 24 cm.
Because there is 4 cm between the circumferences of the two circles, the diameter of the smaller circle must be: 24 - 8 = 16 cm.
The radius of the smaller circle is half its diameter: \dfrac{16}{2} = 8 cm.
Calculate the area of the smaller circle as: \pi \times r^2 = \pi \times 8^2 = 64\pi
The area of the shaded sector is half the area of the smaller circle:
Shaded area = \dfrac{64\pi}{2} = 32\pi cm^2
Marks = 4
Question 5
The table shows information about the annual earnings of 30 people who work in an office.

5(a)
Work out an estimate for the mean of the annual earnings.
ANSWER: Simple Text
Answer: £19600
Workings:
First find the midpoint of the annual earnings for each row.
Multiply the midpoint by the frequency for each row.
The first two steps can be shown in the below table:

Sum all the values for midpoint \times frequency to get:
48000 + 162000 + 220000 + 110000 + 48000 = 588000
Divide this sum by the total frequency to get the mean of the annual earnings:
\dfrac{588000}{30} = £19600
We can calculate this division using the bus stop method, with 588 \div 3 and then adding the required number of zeros:

588 \div 3 = 196\, so 588000 \div 30 = 19600
Marks = 3
5(b)
Which of the following is a reason why the mean might not be the best way to represent the average of this data?
ANSWER: Multiple Choice
A: Outliers will affect the mean value.
B: It takes too long to calculate.
C: It is not possible to calculate the mean using inequalities.
D: The mean gives the most popular value, which there may be more than one of.
Answer: A
Workings:
The mean uses outliers in the data which may give an inaccurate representation of the average.
Marks = 1
Question 6
The area of this rectangle is 64 cm^2

Find the value of x.
ANSWER: Simple Text Answer
Answer: 4 cm
Workings:
4y-4 = 2y+6
2y=10
y=5
Area of rectangle is given by:
(4y-4)x=64
Substitute in y=5:
(20-4)x=64
16x=64
x=4
Marks = 4
Question 7
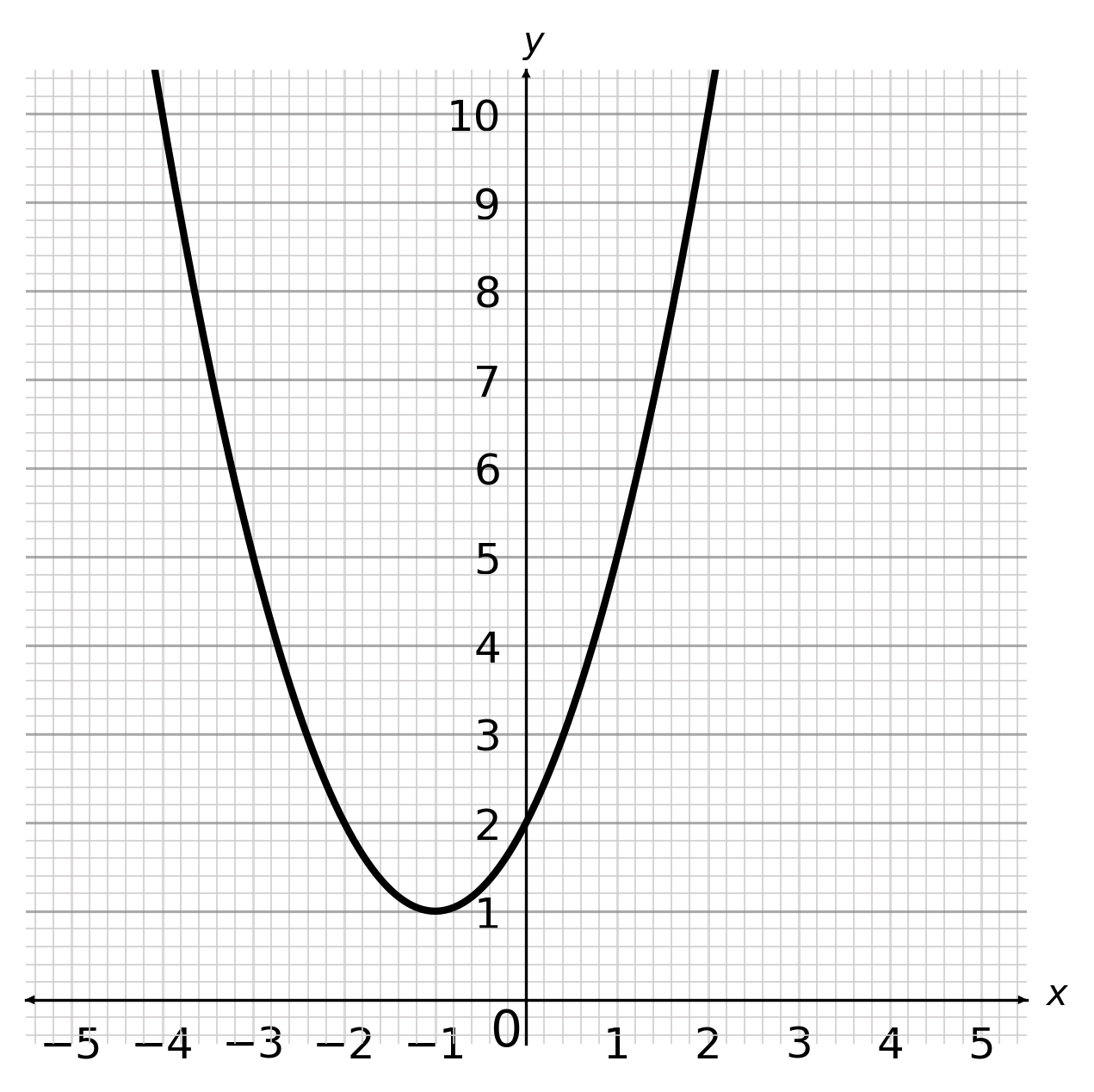
Which of the following is the correct graph for y = x^2+2?
ANSWER: Multiple Choice
A:

B:

C:
D:

Answer: A
Workings:
The graph of y = x^2 + 2 gives a parabola where it reaches the minimum point when x=0 and y=2
Marks = 1
Question 8
Write these numbers in order of size, starting with the largest.
10011\,\,\,\,\,\,\,10101\,\,\,\,\,\,\,10110\,\,\,\,\,\,\,10010\,\,\,\,\,\,\,10111
Answer: Multiple Answers (Correct order required)
Answer:
Largest: 10111
then: 10110
then: 10101
then: 10011
Smallest: 10010
Marks = 2
Question 9
Arthur and Brian cycled along the same 100 km route.
Arthur took 5 hours to complete the journey.
Brian set off fifteen minutes after Arthur, and passed him after 30 km.
Given that they both cycled at constant speeds, what was Brian’s speed to 1 decimal place?
Answer: Simple Text Answer
Answer: 24 km/h
Workings:
First calculate Arthur’s speed:
Speed =\dfrac{\text{Distance}}{\text{Time}} = \dfrac{100}{5} = 20 km/h
Use this value to then calculate the time at which Arthur reaches 30 km:
Time = \dfrac{\text{Distance}}{\text{Speed}} = \dfrac{30}{20} = 1.5 hours
Find the time taken for Brian to reach this point by subtracting 15 minutes from Arthur’s time:
1.5-\dfrac{1}{4} = 1.25 hours
Use these values for time and distance to find Brian’s speed:
Speed =\dfrac{30}{1.25} = 24 km/h
Marks = 5
Question 10
10(a)
What is the value of 64^{\frac{1}{3}}?
Answer: Simple Text Answer
Answer: 4
Workings:
64^{\frac{1}{3}} = \sqrt[3]{64} = 4Marks = 1
10(b)
What is the value of 16^{\frac{3}{4}}?
Answer: Simple Text Answer
Answer: 8
Workings:
16^{\frac{3}{4}} = (16^{\frac{1}{4}})^3 = (\sqrt[4]{16})^3 = 2^3 = 8Marks = 2
Question 11
A café sells fizzy drinks.
3 cans of Fizzy Apple and 4 cans of Fizzy Blackberry cost \pounds 4.80
4 cans of Fizzy Apple and 3 cans of Fizzy Blackberry cost \pounds 5.00
Find the individual costs of a can of Fizzy Apple and a can of Fizzy Blackberry, in pounds (£).
Answer: Multiple Answers (In order)
Answer:
Fizzy Apple = \pounds 0.80
Fizzy Blackberry = \pounds 0.60
Workings:
Write the two statements as equations:
Equation 1: \,\,\,3A + 4B = 4.8
Equation 2: \,\,\,4A + 3B = 5
Multiply Equation 1 by 4 and Equation 2 by 3 to get:
Equation 3: \,\,\,12A + 16B = 19.2
Equation 4: \,\,\,12A + 9B = 15
Subtract Equation 4 from Equation 3 to get:
7B = 4.2
B = 0.6
Substitute B=0.60 into Equation 1 to find A:
3A + 4\times 0.60 = 4.8
3A = 2.4
A = 0.8
So a can of Fizzy Apple costs \pounds 0.80 and a can of Fizzy Blackberry costs \pounds 0.60
Marks = 4
Question 12
The table shows information about the heights, in cm, of a number of trees in Ashton Forest.

12(a)
Which of the following box plots represents the above data?
ANSWER: Multiple Choice
A:

B:

C:

D:

Answer: A
Workings:
The largest value can be calculated as:
Range + Smallest Value =87+64 = 151
The Upper Quartile can be calculated as:
Lower Quartile + IQR =112+24 = 136
You can then plot the lowest value, lower quartile, median, upper quartile and highest value to show the box plot.
Marks = 3
12(b):
The box plot below shows information about the heights, in cm, of a group of trees at Bloomsbury Forest.

Which statement below gives a comparison between the distributions of tree heights in Ashton and Bloomsbury?
ANSWER: Multiple Choice
A: Ashton has a higher median and a higher range.
B: Ashton has a higher median and a lower range.
C: Ashton has a lower median and a higher range.
D: Ashton has a lower median and a lower range.
Answer: A
Workings:
Look at the highest and lowest points to compare the range and the median lines to compare the medians.
Marks = 2
Question 13
13(a):
There are 300 blue or red counters in a bag.
Ahmed picks 10 out of the bag at random as a sample.
The proportion of counters in the sample that are blue is the same as the proportion of counters in the whole bag that are blue.
Ahmed’s sample contains 6 blue counters.
How many blue counters would he expect there to be in the bag in total?
Answer: Simple Text Answer
Answer: 180
Workings:
6 of the 10 counters Ahmed picks out are blue.
This suggests that \dfrac{6}{10} counters are blue.
Applying this to the full bag means the number of blue counters can be calculated as:
\dfrac{6}{10}\times 300 = 180Marks = 2
13(b):
Ahmed has another bag of 300 counters with either red or blue counters in.
For this bag, the number of red counters Ahmed needs is 4 to the nearest whole number, from a sample of 10 counters.
The proportion of counters in the sample that are blue is the same as the proportion of counters in the whole bag that are blue.
Jamie takes a random counter from the bag.
Calculate the lower bound of the probability that the counter is red in its simplest form.
ANSWER: Fraction
Answer: \dfrac{7}{20}
Workings:
The lower bound of 4 to the nearest whole number is 3.5
The proportion of counters in the sample that are red is \dfrac{7}{20}
So the lower bound of the probability that the counter is red is \dfrac{7}{20}
Marks = 2
Question 14
The ratio: (2x+y):(x-2y) is equivalent to k:1
Which of the following is an equation for finding y?
ANSWER: Multiple Choice
A: y= \frac{x(k-2)}{2k+1}
B: y= \frac{2x(k-2)}{k+1}
C: y=\frac{x(k-1)}{k+1}
D: y=\frac{x(k-1)}{2k+1}
Answer: A
Workings:
\dfrac{2x+y}{k} = \dfrac{x-2y}{1}
2x+y = k(x-2y)
2x+y = kx - 2ky
2ky + y = kx-2x
y(2k+1) = x(k-2)
y = \dfrac{x(k-2)}{2k+1}
Marks = 3
Question 15
x = 6.5\dot{4} \dot{5}
Write x as a fraction.
Do NOT simplify your answer.
ANSWER: Fraction
Answer: \dfrac{6480}{990}
Workings:
10x = 65.\dot{4} \dot{5}
1000x = 6545.\dot{4} \dot{5}
1000x - 10x = 6545\dot{4} \dot{5}-65.\dot{4} \dot{5} = 6480 = 990x
x = \dfrac{6840}{990}
Marks = 3
Question 16
y is directly proportional to x^{\frac{3}{2}}
y = 160 when x = 16
Find the value of y when x = 4
ANSWER: Simple Text Answer
Answer: 20
Workings:
y = kx^{\frac{3}{2}}
160 = k\times 16^{\frac{3}{2}}
160 = 64k
k = \dfrac{160}{64} = 2.5
y = 2.5x^{\frac{3}{2}}
For x = 4:
y = 2.5\times 4^{\frac{3}{2}}
y = 2.5\times 8 = 20
Marks = 3
Question 17
Prove algebraically that the product of any two odd numbers is always odd.
Choose the correct proof.
ANSWER: Multiple Choice
A: (2m + 1)(2n + 1) = 4mn + 2m + 2n + 1 = 2(2mn +m + n) + 1 which is odd.
B: (2n + 1)(2n + 1) = 4n^2 + 4n + 1 = 4(n^2 + n) + 1 which is odd.
C: (2m)(2n) = 4mn which is odd.
D: (2n)(2n) = 4n^2 which is odd.
Answer: A
Marks = 2
Question 18
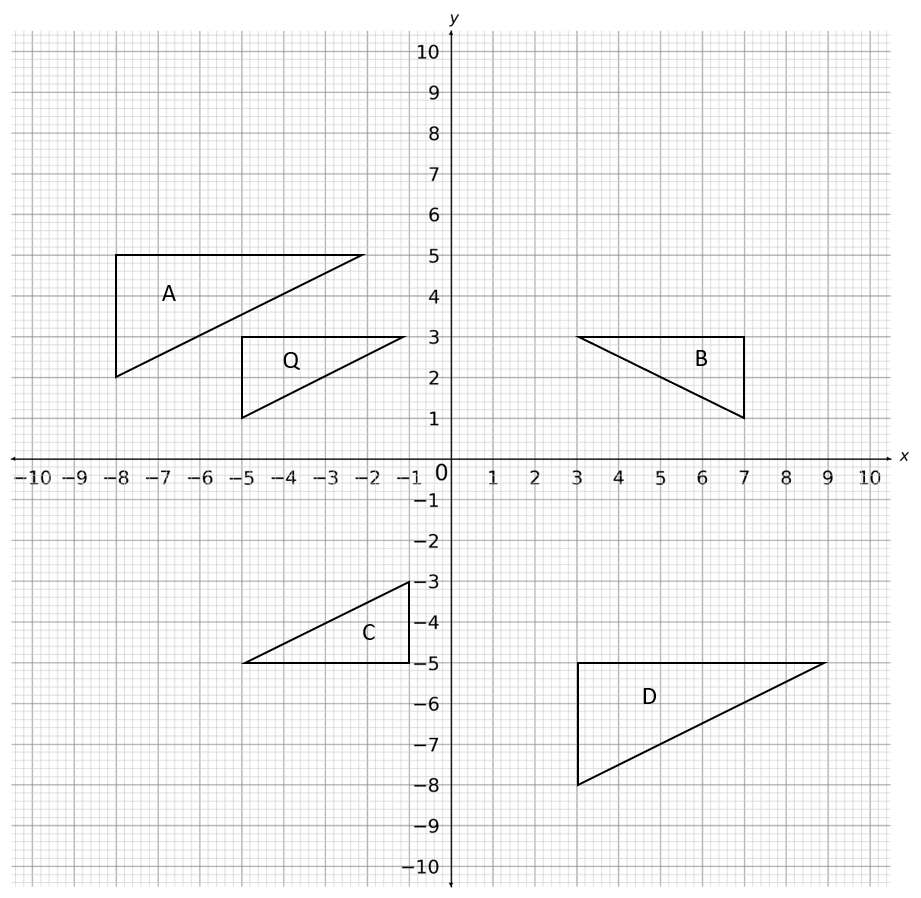
Which shape gives an enlargement of Shape Q with scale factor \dfrac{3}{2} and centre of enlargement (1,-1)?
ANSWER: Multiple Choice
A: Shape A
B: Shape B
C: Shape C
D: Shape D
Answer: A
Workings:
Draw three ray lines connecting the centre of enlargement, (1,-1), with each corner of the triangle.
Calculate the x and y distance of each point of the line from the centre of enlargement.
Multiply these distances by the scale factor, \dfrac{3}{2}, to get the new distances of the points from (1,-1)
The point (-5,1) is 6 places to the left and 2 above.
Multiplying it by \dfrac{3}{2} gives a new point 9 places to the left and 3 above, giving the point (-8,2)
The point (-5,3) enlarges to (-8,5) and (-1,3) enlarges to (-2,5)
This means the enlarged shape must be Shape A.
Marks = 2
Question 19

The graph above shows the rectangle ABCD.
The line P passes through the points B and C.
The line Q passes through the points C, E and D and has equation x + y = 2
The coordinates of Point D are (4,-2).
ED = 2CE
Find an equation for line P.
ANSWER: Multiple Choice
A: y - x = 6
B: y - x = 4
C: x + y = 4
D: x + y = 6
Answer: A
Workings:
x+y=2 can be written as y = -x + 2
Using x=0 gives the point E as (0,2)
CE = \dfrac{1}{2}ED gives the coordinates of C as (-\dfrac{4}{2}, 2+\dfrac{4}{2}) = (-2, 4)
The gradient of line Q is -1
Line P is perpendicular to line Q, so the gradient of P must be the negative reciprocal, which is 1
This gives an initial equation for line P as y = x + k where k is a constant to be found.
The coordinates for C can be substituted in to find k.
4 = -2 + k\,\, so \,\,k = 6
Therefore the equation of line P is y=x+6\,\, or \,\,y-x=6
Marks = 4
Question 20
The table below shows values of x and y that satisfy the equation y=a\, \text{sin}(x)-b

Find the value of y when x = 45
ANSWER: Multiple Choice
A: \dfrac{3\sqrt{2}}{2}-2
B: \dfrac{3\sqrt{3}}{2}-2
C: \dfrac{\sqrt{3}}{2}-2
D: \dfrac{2\sqrt{3}}{3}-2
Answer: A
Workings:
Remembering your trigonometry common values:
\sin (0) = 0
\sin (90) = 1
\sin (45) = \dfrac{\sqrt{2}}{2}
When x=0
y = -b = -2
So b=2
When x=90
y=a-2=1
So a=3
y = 3\, \text{sin}(45)-2
y = \dfrac{3\sqrt{2}}{2}-2
Marks = 4
Question 21
Write \dfrac{4-\sqrt{5}}{\sqrt{5}-2} in the form a + b\sqrt{5} where a and b are both integers.
ANSWER: Multiple Choice
A: 3+2\sqrt{5}
B: 4+3\sqrt{5}
C: 4+2\sqrt{5}
D: 3+3\sqrt{5}
Answer: A
Workings:
Multiply both sides of the fraction by \sqrt{5}+2
\dfrac{4-\sqrt{5}}{\sqrt{5}-2}=\dfrac{(4-\sqrt{5})(\sqrt{5}+2)}{(\sqrt{5}-2)(\sqrt{5}+2)} = \dfrac{4\sqrt{5}+8-5-2\sqrt{5}}{5+2\sqrt{5}-2\sqrt{5}-4} = \dfrac{3+2\sqrt{5}}{1} = 3+2\sqrt{5}Marks = 3
Question 22
The two triangles in the diagram are similar.
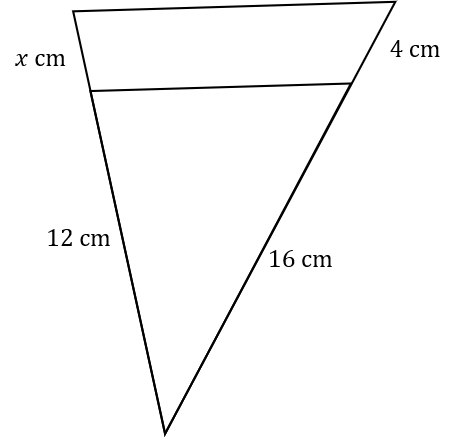
There are two possible values of x
Work out each of these values.
ANSWER: Multiple Choice
A: x=3\,\, or \,\,x=\dfrac{44}{3}
B: x=3\,\, or \,\,x=\dfrac{37}{3}
C: x=2\,\, or \,\,x=\dfrac{44}{3}
D: x=2\,\, or \,\,x=\dfrac{37}{3}
Answer: A
Workings:
To find the first value of x:
Scale factor = \dfrac{16}{4}
x = 12 \times \dfrac{4}{16} = 3
To find the second value of x:
x = \dfrac{20}{12}\times 16 - 12 = \dfrac{320}{12} - 12 = \dfrac{80}{3} - \dfrac{36}{3} = \dfrac{44}{3}
Marks = 5
Question 23
Here is a right-angled triangle and a rectangle, both measured in centimetres:

The right-angled triangle has a greater area than the rectangle.
Find the set of possible values for x.
ANSWER: Multiple Choice
A: x>5; x<1
B: x>5; x<-1
C: x>1; x<-5
D: x>-1; x<-5
Answer: A
Workings:
Calculate the area of the triangle:
\dfrac{1}{2} (2x-2)(2x-5) = \dfrac{1}{2} (4x^2-14x+10) = 2x^2-7x+5
Calculate the area of the rectangle:
x(x-1) = x^2-x
Create an inequality using the two areas:
2x^2-7x+5>x^2-x
x^2-6x+5>0
(x-5)(x-1)>0
This means that the values of x for which the right-angled triangle has a greater area than the rectangle are:
x<1\,\, and \,\, x>5
(5 marks)
