2. November 17 Higher Paper 2

NOTE: Q1-8 are the same as Q16-23 on Nov 17 Foundation Paper 2

(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)

---

Question 1

Solve $4(x+4) = 2(3x+1)$

 

ANSWER: Simple Answer

Answer: $x=7$

Workings:

Expanding the brackets:

$4x+16 = 6x+2$

$2x=14$

$x=7$

Marks = 3

---

Question 2

Mark buys $50$ packs of Toilet Roll for $\pounds 120.00$ total.

He then sells the packs individually at $\pounds 2.90$ each.

Calculate the percentage profit that Mark makes to $1$ decimal place.

 

ANSWER: Simple Answer

Answer: 20.8 %

Workings:

Calculate the total sale price for all $50$ packs of toilet roll:

$50\times \pounds 2.90 = \pounds 145$

Divide this value by the original purchase price of all the toilet rolls and multiply by $100$ to get the percentage of the original amount:

$\dfrac{145}{120} = 120.8\%$

 

So the percentage profit is $120.8-100=20.8\%$

---

Question 3

Suraj walks around a circle, starting at point $A$ and making a complete cycle through all six points, which are equally spaced apart.

The distance between points $A$ and $B$ is $15$ metres.

Calculate the radius of the circle to $1$ decimal place.

 

ANSWER: Simple Answer

Answer: 14.3 metres

Workings:

Calculate the circumference of the circle:

$15\times 6 = 90$ metres

 

Use the formula:

$\text{circumference} = \pi \times \text{diameter}$

to find the diameter.

 

$\text{diameter} = \dfrac{\text{circumference}}{\pi} = \dfrac{90}{\pi} = 28.648$ metres

$\text{radius} = \dfrac{\text{diameter}}{2} = \dfrac{28.648}{2} = 14.3$ metres to $1$ dp.

Marks = 3

---

Question 4

There are a number of coloured fish in a pond.

The fish are either Yellow, Red or Blue.

 

There are three times as many Yellow fish as Red fish.

There are six times as many Blue fish as Yellow fish.

 

Elliot catches a random fish from the pond before putting it back.

What’s the probability that Elliot catches a Red fish?

ANSWER: Fraction

Answer: $\dfrac{1}{22}$

Working:

The two statements can be written as equations:

$Y = 3R\\$

$B=6Y$

 

This can then be written as a ratio in the form Yellow : Red : Blue

$3 : 1 : 18$

 

This gives a probability of $\dfrac{1}{3+1+18} = \dfrac{1}{22}$ of Elliot catching a Red fish.

Marks = 3

---

Question 5

The diagram below shows shape $A$ on a graph.

Which shape on the diagram below shows $A$ having been rotated $180\degree$ around point $(1,1)$?

ANSWER: Multiple Choice

A: Shape P

B: Shape Q

C: Shape R

D: Shape S

Answer: C

Workings:

Using the bottom left corner of the triangle as a focus point, it is $1$ space to the right and $3$ above the centre of rotation.

Because the shape is being rotated $180\degree$ the new shape will have this point $1$ to the left and $3$ below.

It is then possible to find the other two points the same way, to give Shape R as the correct shape.

Marks = 2

---

Question 6

6(a):

$\dfrac{a^7}{a^x} = a^5$

Find the value of $x$.

 

ANSWER: Simple Answer

Answer: x = 2

Workings:

$\dfrac{a^7}{a^x} = a^{7-x} = a^5$

$7-x = 5$

$x = 2$

Marks = 1

 

6(b)

$(b^y)^2 = b^8$

Find the value of $y$.

 

ANSWER: Simple Answer

Answer: y = 4

Workings:

$(b^y)^2 = b^{2y} = b^8$

$2y = 8$

$y = 4$

Marks = 1

 

6(c):

$1000^y \times 100^{2y} = 10^{35}$

Find the value of $y$.

ANSWER: Simple Text Answer

Answer: y = 5

Workings:

$1000^y = (10^3)^y = 10^{3y}$

$100^{2y} = (10^2)^{2y} = 10^{4y}$

$1000^y \times 100^{2y} = 10^{3y} \times 10^{4y} = 10^{35}$

$3y + 4y = 7y = 35$

$y = 5$

Marks = 2

---

Question 7

The diagram below, $ABCD$, represents a trapezium.

Find the angle $BCD$, giving your answer to $1$ decimal place.

 

ANSWER: Simple Answer

Answer: 138.5$\degree$

Workings:

Call the section of side $AB$ that is adjacent to $AD$ and the $6$ cm side: side $x$

To find $x$, use Pythagoras

$\sqrt{11^2 - 6^2} = \sqrt{85}$

 

To calculate the section at the other end of $AB$:

$45 - \sqrt{85} - 29 = 6.78$ cm

 

To find the angle $CB$ makes with the perpendicular:

$\tan^{-1}(\dfrac{6.78}{6}) = 48.493\degree$

Add $90$ to this to get the full angle $BCD$

$90 + 48.493 = 138.5\degree$ to $1$ dp.

Marks = 5

---

Question 8

8(a):

Using a calculator, work out $\dfrac{\cos(40\degree) + \cos(20\degree)}{\sin(40\degree) - \sin(20\degree)}$

Write down all figures on the calculator display.

 

ANSWER: Simple Answer

Answer: 5.67128182

Marks = 2

 

8(b):

Type your answer to part (a) to $2$ decimal places.

ANSWER: Simple Answer

Answer: 5.67

Marks = 1

---

Question 9

It takes $8$ lumberjacks $12$ days to cut down all the trees in Apple Forest.

The following year, there are only $6$ lumberjacks available to cut down all the trees in Blueberry Forest, which has the same number of trees as Apple Forest..

Each lumberjack cuts down $24$ trees a day.

How many trees will each lumberjack cut down in Blueberry Forest?

ANSWER: Simple Answer

Answer: 384

Workings:

$8\times 12 = 96$ days for one person to cut down the forest.

$\dfrac{96}{6} = 16$ days for $6$ lumberjacks to cut down the forest.

$24\times 16 = 384$ gives the number of trees each lumberjack will cut down in Blueberry Forest.

Marks = 3

---

Question 10

Below is a distance-time graph for a car journey.

10(a):

Between which two times was the car going at the fastest speed?

 

ANSWER: Multiple Choice

A: $0 - 20$ s

B: $20 - 40$ s

C: $40 - 60$ s

D: $60 - 80$ s

Answer: B

Workings:

Because this is a distance-time graph, the speed is given by the gradient $\dfrac{\text{distance}}{\text{time}}$

The gradient is steepest between $20$ and $40$ seconds, so this is when the car is going the fastest.

Marks = 2

 

 

 

10(b):

What is the greatest speed of the car?

ANSWER: Simple Answer

Answer: 30 m/s

Workings:

The car is going fastest between $20$ and $40$ s.

The speed for this section can be found by calculating the gradient of the line.

$\text{Speed} = \dfrac{\text{Distance}}{\text{Time}} = \dfrac{\text{change in }y}{\text{change in }x} = \dfrac{600}{20} = 30$ m/s

Marks = 1

---

Question 11

The two pie charts below show the number of pets owned by children at two different primary schools, Bow Ness and Walls End.

The ratio of the number of children at Bow Ness school to the number of children at Walls End school is given by the ratio of the areas of the pie charts.

Find the proportion of the total number of children of the two schools combined attend Bow Ness school and have $2$ – $3$ pets?

Give your answer as a percentage to $3$ significant figures.

The Bow Ness pie chart has radius $4$ and the Walls End pie chart has radius $3$. The $2$ – $3$ pets sector for Bow Ness has angle $100\degree$.

 

ANSWER: Simple Answer

Answer: 17.8 %

Workings:

Calculate the area of each pie chart:

Bow Ness $=16\pi$

Walls End $=25\pi$

 

Calculate the proportion:

$\dfrac{100}{360} \times \dfrac{16\pi}{25\pi} = 0.1778$

Multiply by $100$ to get the answer as a percentage.

$0.1778\times 100 = 17.8\%$ to $3$ significant figures.

Marks = 3

---

Question 12

$AB$ and $BC$ are two sides of a regular $18$-sided polygon.

A line can be drawn between the points $B$ and $C$ to give triangle $ABC$.

Calculate the angle $ACB$.

 

ANSWER: Simple Answer

Answer: 10$\degree$

Workings:

Calculate the exterior angle of the shape.

$\dfrac{360}{18} = 20\degree$

 

The interior angle must therefore be $180 - 20 = 160\degree$

 

Because $AB$ and $AC$ are the same length, $ABC$ must be isosceles.

$ACB = \dfrac{180-160}{2} = 10\degree$

Marks =  3

 

---

 

Question 13

 

Question 13(a) [2 marks]

At the beginning of $2013$, Mr Wiltshire bough a house.

The value of the house was $£80000$

Each year the value of the house increased by $1.5\%$

 

Calculate the value of the house at the beginning of $2020$

Give your answer to the nearest $£1000$

 

Answer type: Simple text answer

ANSWER: £89000

WORKING:

$£80000 \times 1.015^7 = £88787.59 = £89000$ (nearest $£1000$)

 

 

 

Question 13(b) [3 marks]

At the beginning of $2013$ the value of a different house was $£200000$

In $5$ years the value of this house increased to $£220000$

This is equivalent to an increase of $x \%$ each year.

Find the value of $x$.

Give your answer to $2$ decimal places.

 

Answer type: Simple text answer

ANSWER: x = 1.92 $\%$

WORKING:

Let $y = 1+x$

$y^5 \times 200000 = 220000$

$y^5 = \dfrac{220000}{200000} = 1.1$

$y = \sqrt[5]{1.1} = 1.0192448...$

$x = 1.0192448... - 1 = 0.0192448... = 1.92 \%$ ($2$ dp)

 

---

 

Question 14

Which graph correctly shows the region, $R$, that satisfies all of the following inequalities?

 

$y \leq 2x \,\,\,\,\,\,\,\,\,\,\, y + \dfrac{1}{2} x < 4 \,\,\,\,\,\,\,\,\,\,\, y > 2$

 

Answer type: Multiple choice type 1

A:

B:

C:

D:

 

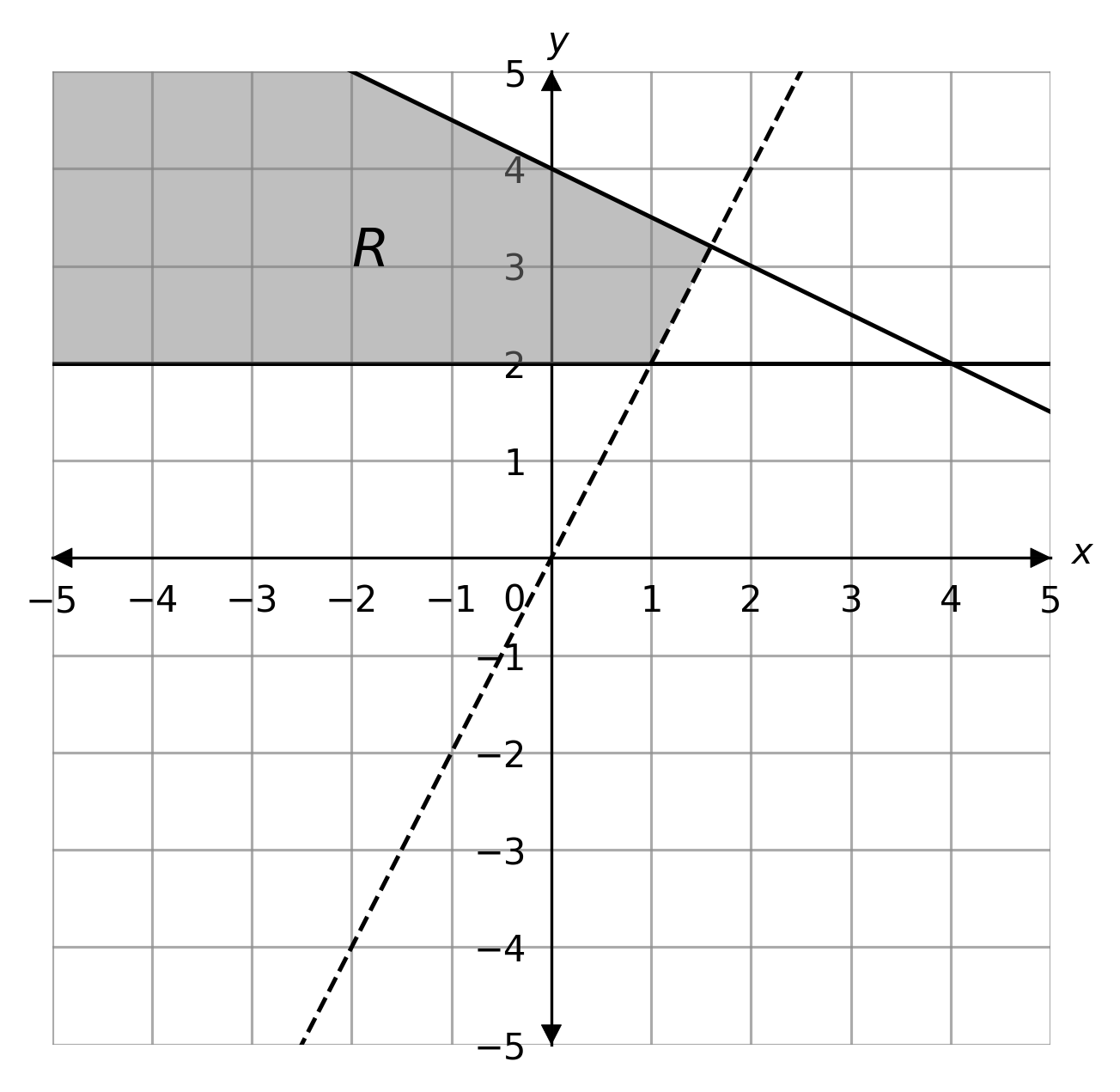
ANSWER: A

WORKING:

$y \leq 2x$ means that we shade the region below the line $y = 2x$, and give it a solid line.

$y + \dfrac{1}{2}x < 4$ means that we shade the region below the line $y = - \dfrac{1}{2}x + 4$, and give it a dashed line.

$y>2$ means that we shade the region above the line $y = 2$, and give it a dashed line.

 

---

 

Question 15

 

Question 15(a) [1 mark]

Bobby is going to choose a sandwich and a drink from a shop.

He can choose from $6$ sandwiches and $4$ drinks.

Which equation would you use to find the number of different ways of choosing a sandwich and a drink?

 

Answer type: Multiple choice type 1

A: $6 \times 4 = 24$ ways

B: $6 + 4 = 10$ ways

C: $6^4 = 1296$ ways

D: $(6 \times 4) \div 2 = 12$ ways

 

ANSWER: A

 

 

 

Question 15(b) [2 marks]

$10$ teams play in a competition.

Each team plays each other once.

How many games are played in total?

 

Answer type: Simple text answer

ANSWER: 45

WORKING:

$10 \times 9 = 90$

$90 \div 2 = 45$ games in total

 

---

 

Question 16 [2 marks]

Solve $(y-3)^2 = 5$

Give your answers to $2$ decimal places.

 

Answer type: Multiple answers type 2 (Can be either way around)

ANSWERS:

y = 5.24

y = 0.76

 

WORKING:

$(y-3)^2 = 5$

$y-3 = \pm \sqrt{5}$

$y = 3 \pm \sqrt{5}$

$y = 5.24$ or $y = 0.76$

 

---

 

Question 17

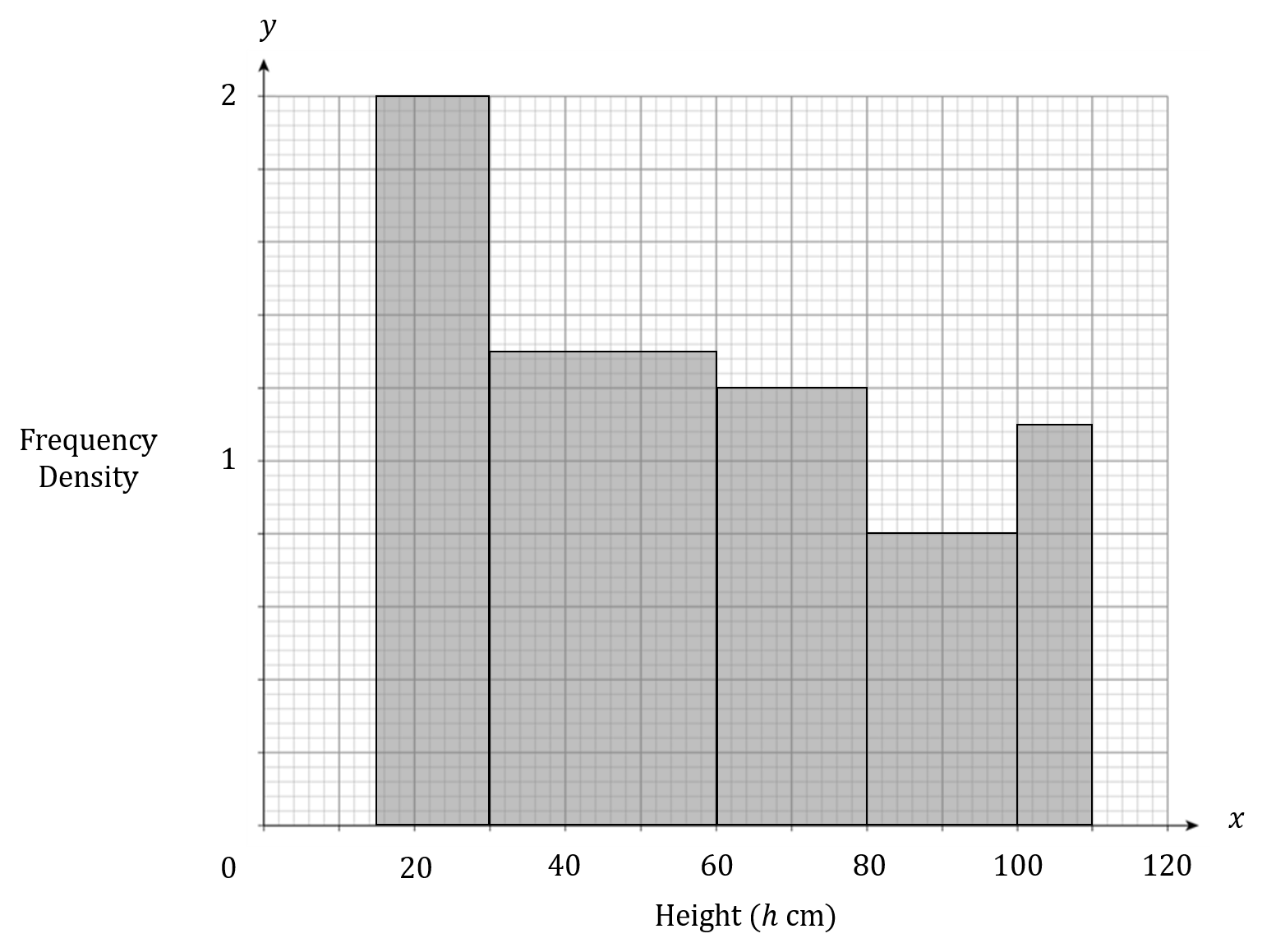
The table below gives information about the heights of $120$ dogs.

 

Question 17(a) [3 marks]

Choose the correct histogram drawn using this information.

 

Answer type: Multiple choice type 1

A:

B:

C:

D:

 

ANSWER: A

WORKING:

With lengths on the $x$-axis and frequency density on the $y$-axis, we draw each bar with width equal to its class width, and height equal to the corresponding frequency density.

 

 

Question 17(b) [2 marks]

Work out an estimate for the fraction of the dogs that have a height between $40$ cm snd $90$ cm

Give your answer in its simplest form.

 

Answer type: Fraction

ANSWER: $\dfrac{29}{60}$

WORKING:

Number of dogs in interval $= \bigg(\dfrac{2}{3} \times 39\bigg) + 24 + \bigg(\dfrac{1}{2} \times 16\bigg) = 58$

Fraction $= \dfrac{58}{120} = \dfrac{29}{60}$

 

---

 

Question 18 [1 mark]

At time $t = 0$ days a tank is full of oil.

Oil is used from the tank.

At the end of every day there is $3\%$ less oil in the tank than at the start of the day.

The volume of oil, in litres, in the tank at time $t$ days is $V_t$

Given that

$V_0 = 5000$

$V_{t+1} = k V_t$

find the value of $k$

 

Answer type: Simple text answer

ANSWER: 0.97

WORKING:

$1 - 0.03 = 0.97$

 

---

 

Question 19 [4 marks]

A triangle has vertices $A$, $B$ and $C$.

The coordinates of $A$ are $(-2,-5)$

The coordinates of $B$ are $(2,3)$

The coordinates of $C$ are $(6,-3)$

$M$ is the midpoint of $AB$

$N$ is the midpoint of $BC$

 

Choose the correct statement regarding this information.

 

Answer type: Multiple choice type 2

A: $\overrightarrow{MN}$ is half the length of $\overrightarrow{AC}$, and is parallel to $\overrightarrow{AC}$

B: $\overrightarrow{MN}$ is twice the length of $\overrightarrow{AC}$, and is parallel to $\overrightarrow{AC}$

C: $\overrightarrow{MN}$ is twice the length of $\overrightarrow{AC}$, and is perpendicular to $\overrightarrow{AC}$

D: $\overrightarrow{MN}$ is half the length of $\overrightarrow{AC}$, and is not parallel to $\overrightarrow{AC}$

 

ANSWER: A

WORKING:

$\overrightarrow{AC} = \begin{pmatrix}6-(-2)\\-3-(-5)\end{pmatrix} = \begin{pmatrix}8\\2\end{pmatrix}$

 

$M = \bigg( \dfrac{-2+2}{2} , \dfrac{3-5}{2} \bigg) = (0,-1)$

$N = \bigg( \dfrac{2+6}{2} , \dfrac{3-3}{2} \bigg) = (4,0)$

 

$\overrightarrow{MN} = \begin{pmatrix}4-0\\0-(-1)\end{pmatrix} = \begin{pmatrix}4\\1\end{pmatrix} = \dfrac{1}{2}\begin{pmatrix}8\\2\end{pmatrix} = \dfrac{1}{2} \overrightarrow{AC}$

 

Hence, $\overrightarrow{MN}$ is half the length of $\overrightarrow{AC}$, and is parallel to $\overrightarrow{AC}$

 

---

 

Question 20 [5 marks]

 

$OABC$ is a sector of a circle, centre $O$

$AD$ is the tangent to the circle at point $A$

$CD$ is the tangent to the circle at point $C$

Angle $CDE = 120 \degree$

$CD = 8$ cm

 

Calculate the area of the shaded region.

Give your answer correct to $2$ decimal places.

 

Answer type: Simple text answer

ANSWER: 44.68 cm$^2$

WORKING:

$\angle ADC = 180 - 120 = 60 \degree$ (angles on a straight line)

$\angle OCD = 90 \degree$ (radius meeting tangent to circle)

We can split the shape $AOCD$ into two equal right-angled triangles, then

$\angle CDO = 60 \div 2 = 30 \degree$

$\angle COD = 180 - 90 - 30 = 60 \degree$

 

Similarly $\angle OAD = 90 \degree$, $\angle ADO = 30 \degree$ and $\angle AOD = 60 \degree$

 

 

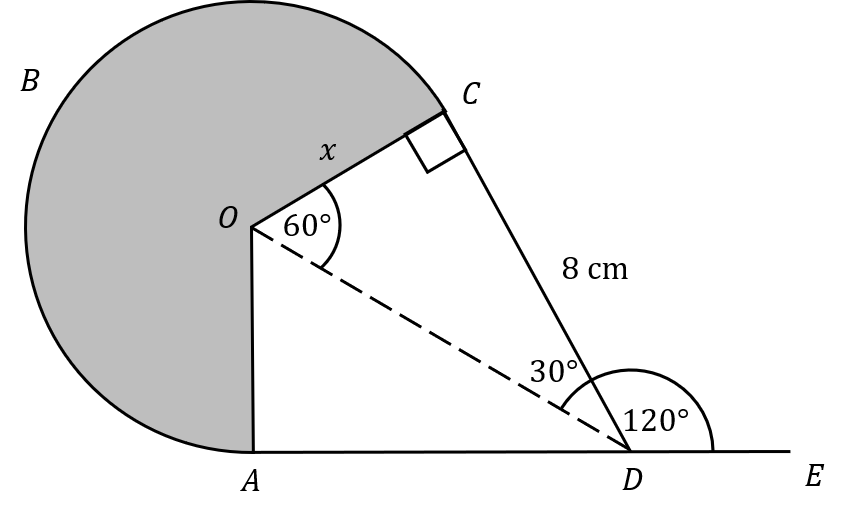
We then need to find the length $OC$, call it $x$. This is the radius of the sector.

Using SOHCAHTOA,

$\tan 30 = \dfrac{x}{8}$

$x = 8 \tan 30 = \dfrac{8 \sqrt{3}}{3}$ cm

 

Reflex angle $AOC = 360 - 60 - 60 = 240 \degree$

Now, we can find the area of the sector (the shaded region)

Area of sector $= \dfrac{240}{360} \times \pi \times \bigg(\dfrac{8 \sqrt{3}}{3} \bigg)^2 = \dfrac{128}{9} \pi = 44.68$ cm$^2$ ($2$ dp)

 

---

 

Question 21

There are $15$ marbles in a bag.

There is an equal number of pink marbles, green marbles and orange marbles in the bag.

There are no other marbles in the bag.

$2$ marbles are taken at random from the bag.

 

Question 21(a) [2 marks]

Calculate the probability of taking $2$ pink marbles.

Give your answer as a fraction in simplest form.

 

Answer type: Fraction

ANSWER: $\dfrac{2}{21}$

WORKING:

There are $15 \div 3 = 5$ of each colour marble in the bag

Probability $= \dfrac{5}{15} \times \dfrac{4}{14} = \dfrac{20}{210} = \dfrac{2}{21}$

 

 

 

Question 21(b) [2 marks]

The $2$ marbles are put back in the bag.

 

Some more marbles are now taken out of the bag.

There is still an equal number of pink marbles, green marbles and orange marbles in the bag.

There are no marbles of any other colour in the bag.

 

$2$ marbles are taken at random from the bag.

Is it now less likely, equally likely or more likely that the $3$ marbles will be pink?

 

Answer type: Multiple choice type 1

A: Less likely

B: Equally likely

C: More likely

 

ANSWER: A

WORKING:

Say there are now only $12$ marbles, with $4$ of each colour in the bag.

Probability of $2$ pink $= \dfrac{4}{12} \times \dfrac{3}{11} = \dfrac{12}{132} = \dfrac{1}{11} = 0.0909...$

 

Before, the probability was $\dfrac{2}{21} = 0.0952...$, which is larger than $\dfrac{1}{11}$

So, now it is less likely that the $2$ marbles will be pink, since there are less counters in the bag.

 

---

 

Question 22 [5 marks]

The functions $f$ and $g$ are such that

$f(x) = 3x+2\,\,\,\,\,$ and $\,\,\,\,\,g(x) = ax+b$ where $a$ and $b$ are constants

 

$g(2) = 11\,\,\,\,\,$ and $\,\,\,\,\, f^{-1}(53) = g(3)$

 

Find the values of $a$ and $b$

 

Answer type: Multiple answers type 1

ANSWERS:

a = 6

b = -1

 

WORKING:

$g(2) = 11 = 2a+b$

$g(3) = 3a+b = f^{-1}(53)$

 

$f^{-1}(x) = \dfrac{x-2}{3}$

$f^{-1}(53) = \dfrac{53-2}{3} = 17$

 

So, we have two simultaneous equations that we can solve,

$2a+b = 11\,\,\,$ (1)

$3a+b=17\,\,\,$ (2)

 

(2) $-$ (1): $a = 6$

(1) rearranged: $b = 11 - 2a = 11 - 2(6) = -1$

 

$a = 6\,\,$ and $\,\,b = -1$

 

---

 

Question 23

$S$ is a geometric sequence.

 

Question 23(a) [3 marks]

Given that $(\sqrt{x} - 3)$, $1$ and $(\sqrt{x}+3)$ are the first three terms of $S$, find the value of $x$.

 

Answer type: Simple text answer

ANSWER: x = 10

WORKING:

We can express the common ratios algebraically

$\dfrac{1}{\sqrt{x} - 3} = \dfrac{\sqrt{x}+3}{1}$

$1 = (\sqrt{x}+ 3)(\sqrt{x} - 3)$

$1 = x - 9$

$x = 10$

 

 

 

Question 23(b) [2 marks]

The $6$th term can be expressed as $(\sqrt{10} + 3)^a$

Find the value of $a$

 

Answer type: Simple text answer

ANSWER: a = 4

WORKING:

$x = 10$

Common ratio $= (\sqrt{10}+3)$

 

$6$th term $= 3$rd term $\times$ (common ratio)$^3$

$6$th term $= (\sqrt{10}+3) \times (\sqrt{10} + 3)^3 = (\sqrt{10} + 3)^4$

 

So, $a = 4$