Question 1
(3 marks)
The table below shows information about the heights of 90 children.

1(a)
Find the class interval that contains the median.
(1 mark)
Answer: Multiple Choice
Answer: 155<h\le 160
Wrong Answers:
150<h\le 155
160<h\le 165
145<h\le 150
WORKING:
The median of a set of 90 numbers is half way between the 45th and 46th number.
The 45th and 46th number both lie in the interval 155<h\le 160
1(b)
Select which frequency polygon represents the information in the table.
(2 marks)
Answer type: Multiple Choice
Answer:

Wrong Answers:
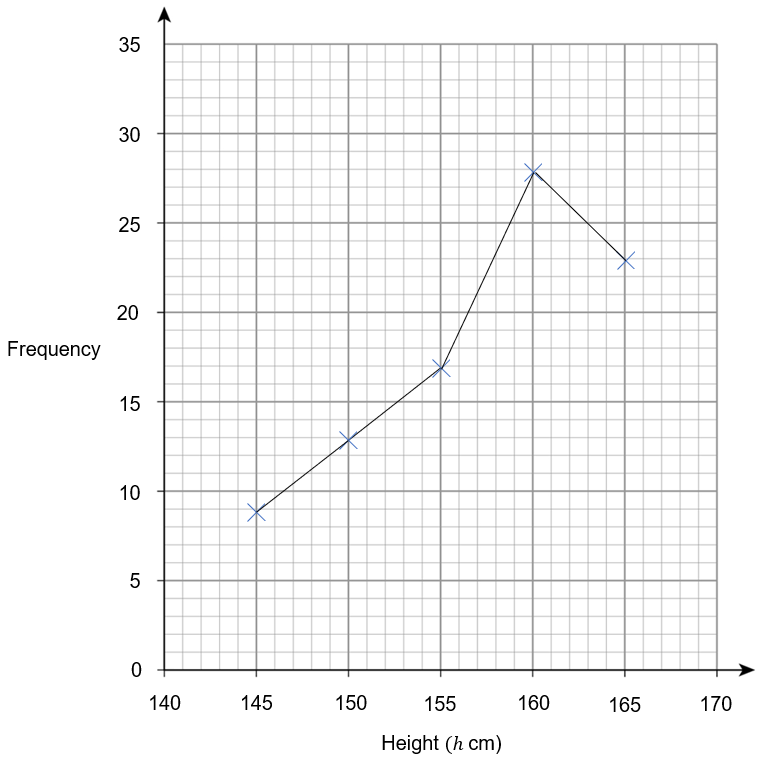


WORKING:
To draw a frequency polygon we first need to find the midpoints of the intervals.
These are: 142.5, 147.5, 152.5, 157.5, 162.5
Then plot these against their respective frequencies.
So we plot the points: (142.5, 9), (147.5, 13), (152.5, 17), (157.5, 28), (162.5, 23)
We then connect these points with straight lines to give us a frequency polygon.
Question 2
(3 marks)
In Dublin, 1 litre of petrol costs 125 cents.
In Washington DC, 1 gallon of petrol costs \$2.62
1 US gallon =3.785 litres.
€1 = \$1.22
In which city is petrol better value for Money?
Answer type: Multiple Choice
Answer: Washington DC
Wrong Answer: Dublin
WORKING:
First we find the price of petrol per gallon in Dublin.
Dublin: 3.785\times1.25= €4.73 per gallon.
4.73\times1.22=\$5.77 per gallon.
We can clearly see that petrol is more expensive in Dublin compared to Washington DC.
Question 3
(3 marks)
A silver bar has a mass of 4.5 kg.
The density of silver is 10.49 g/cm^3.
Work out the volume of the silver bar, giving your answer to 3 significant figures.
Answer type: Simple text
Answer: 429 cm^3
WORKING:
The formula for density is:
Density =\dfrac{\text{Mass}}{\text{Volume}}
We can rearrange this to give us the formula for volume:
Volume =\dfrac{\text{Mass}}{\text{Density}}
Volume =\dfrac{4.5\times1000}{10.49}=429 cm^3 (to 3 significant figures)
Question 4
(3 marks)
There are only yellow, blue and white counters in a bag.
The ratio of the number of yellow counters to blue counters is 1:3
The ratio of the number of blue counters to white counters is 7:5
There are less than 130 counters in the bag.
What is the greatest possible number of white counters in the bag?
Answer type: Simple text
Answer: 45
WORKING:
We first need to convert the two ratios we have into one ratio.
To do this we see that blue counters are in both ratios, so we can combine the ratios by finding the lowest common multiple of 3 and 7, which is 21
Ratio of yellow to blue is 1:3=7:21
Ratio of blue to white is 7:5=21:15
Thus, the ratio of yellow to blue to white is 7:21:15
7+21+15=43=43
\dfrac{130-1}{43}=3
15\times3=45 white counters.
Question 5
(3 marks)
5(a)
Find the reciprocal of 1.25
Give your answer as a decimal.
(1 mark)
Answer type: Simple Text
Answer: 0.8
WORKING:
1\div1.25=1\div\dfrac{5}{4}=1\times\dfrac{4}{5}=0.85(b)
(2 marks)
Kate rounds a number, x, to one decimal place.
The result is 8.7
Write down the error interval for x
Answer type : Multiple Answer
Answer:
x \ge 8.65
x < 8.75
Question 6
(5 marks)
Here is a rectangle.

The length of the rectangle is 9 cm longer than the width of the rectangle.
4 of these rectangles are used to make this 8-sided shape.

The perimeter of the 8-sided shape is 104 cm.
Work out the area of the 8-sided shape.
Answer type: Simple Text
Answer: 280 cm^2.
WORKING:
If we represent the width of the rectangle by x, the length of the rectangle =x+9

As shown by the diagram below the perimeter of the 8-sided shape =x+9+x+x+x+9+x+x+9+x+x+9+9+9+2x=10x+54

10x+54=104
10x=50
x=5
So, we can work out the area of one rectangle:
Area =(x+9)\times x=14\times5=70 cm^2
Total Area = 70\times4=280 cm^2
Question 7
(2 marks)
Work out (12.7\times10^6)\times(4.9\times10^{-11})
Give your answer as an ordinary number.
Answer: Simple Text
Answer: 0.0006223
WORKING:
(12.7\times10^6)\times(4.9\times10^{-11})=6.223\times10^{-4}=0.0006223Question 8
(3 marks)
When a drawing pin is dropped it can land point down or point up.
Sarah, Jack and Mike each dropped the drawing pin a number of times.
The table below shows the number of times the drawing pin landed point down and the number of times the drawing pin landed point up for each person.

Emma is going to drop the drawing pin once.
8(a) Whose results will give the best estimate for the probability that the drawing pin will land point up?
(1 mark)
Answer: Multiple Choice
Answer: Jack
Wrong Answers:
Sarah
Mike
WORKING:
Jack’s results will give the best probability that the drawing pin will land point up because he drops the pin the most times.
8(b) (2 marks)
Oliver is going to drop the drawing pin twice.
Use all the results in the table to work out an estimate for the probability that the drawing pin will land point down the first time and point up the second time.
Answer type: Multiple Choice
Answer: \dfrac{2}{9}
Wrong Answers:
\dfrac{1}{3}
\dfrac{2}{5}
\dfrac{1}{4}
WORKING:
Total number of drops =27+58+15+17+23+10=150
Number of times pin landed point down =27+58+15=100
Number of times pin landed point up =17+23+10=50
Estimate for the probability that the drawing pin will land point down the first time and point up the second time:
\dfrac{100}{150}\times\dfrac{50}{150}=\dfrac{2}{9}Question 9
(5 marks)
Luke bought a new car for £11800
The value, £V, of Luke’s car at the end of n years is given by the formula,
V=11800\times(0.76)^n
9(a) At the end of how many years was the value of Luke’s car first less than 40\% of the value when it was new?
(2 marks)
Answer type: Simple text
Answer: 4 years
WORKING:
Need to find a value of n which satisfies 0.4>0.76^n:
0.76^2=0.5776
0.76^3=0.438976
0.76^4=0.33362176
Hence n=4
9(b)
(3 marks)
A savings account pays interest at a rate of R\% per year.
Luke invests £6600 in the account for one year.
At the end of the year, Luke pays tax on the interest at a rate of 40\%
After paying tax, he gets £150.48
Work out the value of R.
Answer type: Simple text
Answer: 3.8\%
WORKING:
150.48\div0.6=250.8
R = \dfrac{250.8}{6600}\times100=3.8 \%
Question 10
(3 marks)
There are only red pens, black pens, blue pens and green pens in a box.
A pen is taken at random from the box.
The table below shows the probabilities of getting a red, blue or green pen from the box.

10(a)
(1 mark)
Work out the probability of getting a black pen.
Answer type: Simple Text
Answer: 0.4
WORKING:
P(Black) =1-0.15-0.25-0.2=0.4
10(b)
(2 marks)
What is the least number of pens in the box?
Answer type: Simple text
Answer: 20
WORKING:
If we convert all the probabilities into fractions we get:
\dfrac{15}{100}, \dfrac{40}{100}, \dfrac{25}{100}, \dfrac{20}{100}
5 is the highest common factor for 15, 40, 25 and 20
The fractions can then be simplified to \dfrac{3}{20}, \dfrac{8}{20}, \dfrac{5}{20}, \dfrac{4}{20}
So we can see that the least number of pens in the box is 20
Question 11
(4 marks)
The cumulative frequency graph below shows the information about the time taken to get to work of 60 people in an office.
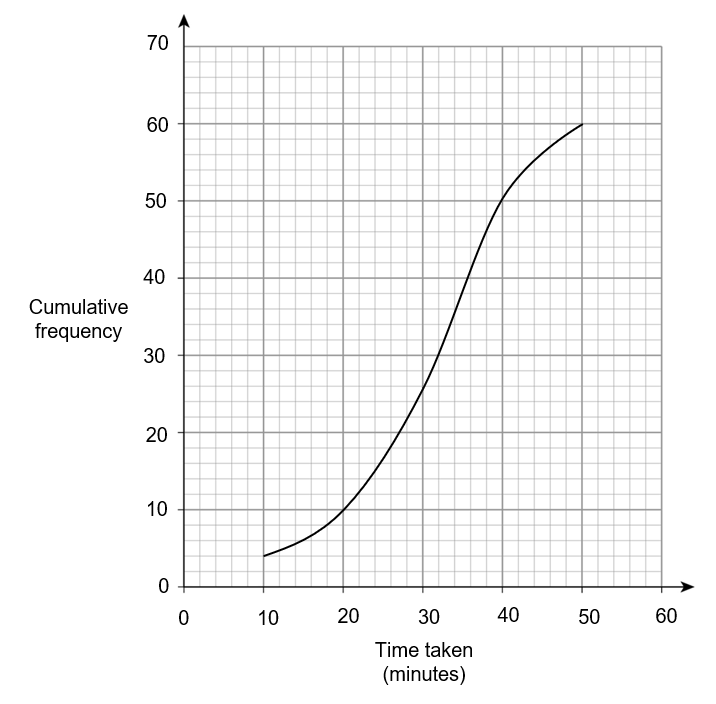
11(a)
Use the graph to find an estimate for the median time taken to get to work.
(1 mark)
Answer type: Simple text
Answer: 32 minutes
WORKING:
To find an estimate for the median read off from the graph at half way along the cumulative frequency values.

As shown on the graph above, we can see that the estimate for the mean is 32 minutes.
11(b)
James says,
“50-10=40 so the range of the journey times is 40 minutes.”
Is James correct?
(1 mark)
Answer type: Multiple choice
Answer: No
Wrong Answer: Yes
WORKING:
The maximum time taken could be less than 50 minutes or the minimum time taken could be more than 10 minutes.
So James may not be correct.
11(c)
How many people have a journey time of more than 40 minutes?
(1 mark)
Answer Type: Simple Text
Answer: 10
11(d)
James also says that,
“Less than 20\% of workers have a journey time of more than 40 minutes.”
Is James correct?
(1 mark)
Answer Type: Multiple Choice
Answer: Yes
Wrong Answer: No
WORKING:
As worked out in part (c), 10 people have a journey time of more than 40 minutes.
\dfrac{10}{60}=16.67\%
16.67\%<20\%
Therefore James is correct.
Question 12
(3 marks)
Lewis has 2 biased coins.
Each coin can only land on heads or tails.
The probability that coin 1 lands on heads is 0.35
The probability that coin 2 lands on heads is 0.7
The probability tree diagram below shows this information.

Lewis flips coin 1 once and flips coin 2 once.
He does this a number of times.
The number of times both coins land on heads is 49
Work out an estimate for the number of times both coins land on tails.
Answer Type: Simple Text
Answer: 39
WORKING:
Probability of both landing on heads =0.35\times0.7=0.245
Probability of both landing on tails =0.65\times0.3=0.195
Estimate for the number of total flips of both coins =\dfrac{49}{0.245}=200
Estimate for the number of times both coins landed on tails =200\times0.195=39
Question 13
(2 marks)
Find the values of a and b where x^2+16x+47=(x+a)^2+b and a and b are integers.
Answer Type: Multiple Answers
Answer:
a=8
b=-17
WORKING:
x^2+16x+47=(x+8)^2-64+47=(x+8)^2-17
So, a = 8 and b = -17
Question 14
(3 marks)
Pyramid A and pyramid B are mathematically similar.
The ratio of the surface area of pyramid A to the surface area of pyramid B is 16:9
The volume of pyramid A is 320 cm^3
What is the volume of pyramid B?
Answer Type: Simple Text
Answer: 135 cm^3
WORKING:
To work out the ratio of the dimensions of pyramid A and pyramid B we take the square root of the ratio of surface areas.
\sqrt{16}=4, \,\, \sqrt{9}=3
To work out the ratio of the volumes we then cube these values.
4^3=64, \,\, 3^3=27
So the ratio of the volume of pyramid A to pyramid B is 64:27
We know that the volume of pyramid A is 320 cm^3,
so the volume of pyramid B is 320\times\dfrac{27}{64}=135 cm^3
Question 15
(9 marks)
15(a)
(2 marks)
Which of the following intervals contains a solution to the equation x^3+6x-10?
Answer type: Multiple choice
Answer: 1 < x < 2
Wrong Answers:
0 < x < 1
2 < x < 3
3 < x < 4
WORKING:
Substituting x=1 into the equation gives: \,\, 1^3+(6\times1)-10=-3
Substituting x=2 into the equation gives: \,\, 2^3+(6\times2)-10=10
Therefore we can see that for a value of x between 1 and 2, x^3+6x-10=0
So, 1 < x < 2 contains a solution to x^3+6x-10
15(b)
(2 marks)
The equation x^3+6x-10=0 can be rearranged into the form x=\dfrac{a}{x^b+c}
Find a, b and c.
Answer Type: Multiple Answer
Answer:
a=10
b=2
c=6
WORKING:
x^3+6x-10=0
x^3+6x=10
x(x^2+6)=10
x=\dfrac{10}{x^2+6}
15(c)
(3 marks)
Starting with x_0=1, use the iteration formula x_{n+1}=\dfrac{10}{{x_n}^2+6} three times to find an estimate for the solution of x^3+6x-10=0
Give your answer to 4 decimal places.
Answer Type: Simple Text
Answer: 1.3251
WORKING:
x_1=\dfrac{10}{1^2+6}=\dfrac{10}{7}
x_2=\dfrac{10}{\frac{10}{7}^2+6}=\dfrac{245}{197}
x_3=\dfrac{10}{\frac{245}{197}^2+6}=1.3251 to 4 decimal places.
15(d)
(2 marks)
Substitute your answer to part (c) into x^3+6x-10
Is the estimate for the solution to x^3+6x-10=0 accurate?
Answer Type: Multiple Choice
Answer: No
Wrong Answer: Yes
WORKING:
Substituting x=1.3251 into x^3+6x-10 we get 0.2773298523
Therefore we can see that this estimate isn’t that close to 0 relative to the size of the interval that we know the solution is in.
Question 16
(3 marks)
Jordan records the distance in kilometres he ran last week and the amount of time spent running.
The average time per 5 km is given by the formula:
Average time per 5 km =\dfrac{5\times\text{total time spent running}}{\text{total kilometres ran}}
Jordan records that he ran 46.6 km last week, correct to 3 significant figures.
He spent 251 minutes running last week, correct to 3 significant figures.
16(a)
(1 mark)
What is the lower bound on the distance travelled by Jordan last week?
Answer Type: Simple Text
Answer: 46.55 km
WORKING:
The smallest number that rounds to 46.6 to 3 significant figures is 46.55
16(b)
(1 mark)
What is the upper bound on the time spent running for Jordan last week?
Answer Type: Simple Text
Answer: 251.5 minutes
WORKING:
Any value between 250.5 and 251.5 rounds to 251 correct to 3 significant figures, including 250.5 and not including 251.5
16(c)
(1 mark)
Jordan says,
“My average time per 5 k was less than 27 minutes last week.”
Could Jordan be wrong?
Answer Type: Multiple Choice
Answer: Yes
Wrong Answer: No
WORKING:
The greatest possible average time per 5 km is:
\dfrac{5\times251.5}{46.55}=27.01396348 minutes
Therefore it is possible that Jordan’s average time per 5 km was greater than 27 minutes.
Question 17
(5 marks)
ABC and ADC are triangles.

The area of triangle ACD is 43 cm^2
Work out the length of BC.
Give your answer to 1 decimal place.
Answer Type: Simple Text
Answer: 9.8 cm
WORKING:
We first need to find the length of DC:
Using the formula: Area of a triangle =\dfrac{1}{2}ab\sin c
We know that,
\dfrac{1}{2}\times7.5\times DC\times \sin96=43
DC=\dfrac{43}{\frac{1}{2}\times7.5\times \sin96}=11.529... cm
Using the cosine rule,
AC^2=7.5^2+(11.529...)^2-2(7.5)(11.529...)\cos96
AC^2 = 207.26...
AC = \sqrt{207.26...} = 14.396... cm
To use the sine rule we need to find the angle \angle BAC:
\angle BAC=180\degree-105\degree-34\degree=41\degree
We can then use the sine rule to find BC:
\dfrac{14.396...}{\sin105}=\dfrac{BC}{\sin41}
BC=\dfrac{14.396...\times \sin41}{\sin105}=9.8 cm to 1 decimal place.
Question 18
Here is a speed-time graph for a car.

18(a)
(3 marks)
Work out an estimate for the distance the car travelled in the first 40 minutes.
Use 4 strips of equal width.
Answer Type: Simple Text
Answer: 370 m
WORKING:
Using the formula for the area of a trapezium we can find the area under the curve for the first 40 seconds.
We use width lengths of 10
Estimate for the area under curve =10\times(\dfrac{0+3}{2}+\dfrac{7+3}{2}+\dfrac{14+7}{2}+\dfrac{26+14}{2})=370 m
18(b)
(1 mark)
Is your answer to (a) an underestimate or an overestimate of the actual distance the car travelled?
Answer Type: Multiple Choice
Answer: Overestimate
Wrong Answer: Underestimate
WORKING:
It is an overestimate as the curve dips below the shape of trapeziums.
Question 19
19(a)
(4 marks)
Find the point of intersection of the circle with equation x^2+y^2=45 and the line y+2x=15
Answer Type: Multiple Answer
Answer:
x = 6
y = 3
WORKING:
We first need to rearrange the equation of the line to make y the subject.
y+2x=15
y=15-2x
We then need to substitute this expression for y into the equation for the circle.
x^2+(15-2x)^2=45
x^2+225-60x+4x^2=45
5x^2-60x+180=0
x^2=12x+36=0
(x-6)^2=0
So the only solution for this equation is x=6
Then substitute this value of x into the expression we have for y
y=15-2(6)=3
Therefore, the point of intersection is (6,3)
19(b)
(1 mark)
What does your answer in part (a) tell you about the line y+2x=15?
Answer Type: Multiple Choice
Answer: The line y+2x=15 is a tangent to the circle x^2+y^2=45
Wrong Answers:
The line y+2x=15 goes through the centre of the circle x^2+y^2=45
The line y+2x=15 also intersects the circle x^2+y^2=45 at the point (-6,-3)
The line y+2x=15 doesn’t intersect the circle x^2+y^2=45 at any point
WORKING:
The line y+2x=15 only intersects the circle x^2+y^2=45 at one point, therefore the line y+2x=15 is a tangent to the circle.
Question 20

A, B and C are points on the circumference of a circle, centre O.
AOB is a diameter of the circle.
20(a)
(1 mark)
If a line OC is added, what type of triangles are ACO and COB?
Answer Type: Multiple Choice
Answer: Isosceles triangles
Wrong Answers:
Equilateral triangles
Right-angled triangles
Scalene triangles
WORKING:

OA, OB and OC are all radii of the circle, hence they are all the same length.
Therefore, ACO and COB are isosceles triangles, as the have two sides the same length.
20(b)
(3 marks)
Hence, find angle \angle ACB
Answer Type: Simple Text
Answer: 90\degree
WORKING:

Angles in triangle add up to 180\degree
Therefore, y+y+x+x+180=360
2x+2y=180
x+y=90
So, \angle ACB=90\degree
Question 21
(5 marks)
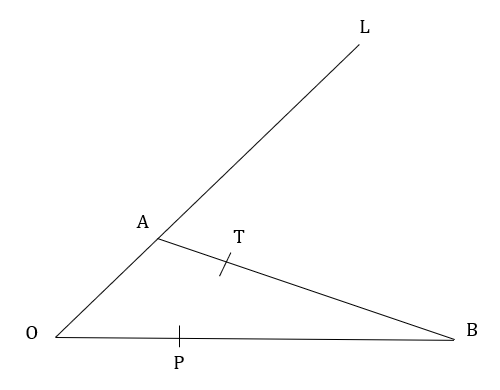
OAL, OPB and ATB are straight lines.
AL = 3OA
2OP=PB
\overrightarrow{OA}=\mathbf{a}\,\,\,\,\,\,\,\,\,\, \overrightarrow{OB}=\mathbf{b}
\overrightarrow{AT}=k\overrightarrow{AB} where k is a scalar quantity.
Given that PTL is a straight line, find the value of k.
Answer Type: Fraction
Answer:\dfrac{3}{11}
WORKING:

Firstly we can see that \overrightarrow{AB}=-\mathbf{a}+\mathbf{b} and \overrightarrow{AT}=k(-\mathbf{a}+\mathbf{b})
\overrightarrow{PL}=-\dfrac{1}{3}\mathbf{b}+4\mathbf{a}
\overrightarrow{TL}=-k(-\mathbf{a}+\mathbf{b})+3\mathbf{a}=-k\mathbf{b}+(k+3)\mathbf{a}
\overrightarrow{PL} must be a multiple of \overrightarrow{TL} as PTL is a straight line.
So \overrightarrow{PL}=x\overrightarrow{TL}, where x is a scalar quantity.
So \overrightarrow{PL}=-\dfrac{1}{3}\mathbf{b}+4\mathbf{a}=-xk\mathbf{b}+x(k+3)\mathbf{a}
Hence by equating the coefficients of \mathbf{a} and \mathbf{b},
we can see that \dfrac{1}{3}=kx and x(k+3)=4
So, x=\dfrac{4}{k+3} and k=\dfrac{1}{3x}
Substituting the expression for x into the expression for k gives:
k=\dfrac{1}{3\times\frac{4}{k+3}}=\dfrac{k+3}{12}
k+3=12k
k=\dfrac{3}{11}
