Note: Questions 23-29 are copied from Q1-7 November 17 Higher Paper 1
Question 1
(2 marks)
1(a)
(1 mark)
Change 485 cm into metres.
Answer Type: Simple Text
Answer: 4.85 m
1(b)
(1 mark)
Change 1.9 kg into grams.
Answer Type: Simple Text
Answer: 1900 g
Question 2
(1 mark)
Work out \,\,5+6\div3
Answer Type: Simple Text
Answer: 7
WORKING:
Using BIDMAS, we first calculate 6\div3
6\div3=2
5+6\div3=5+2=7
Question 3
(1 mark)
Solve \,\,\dfrac{t}{5.5}=11
Answer Type: Simple Text
Answer: t=60.5
WORKING:
\dfrac{t}{5.5}=11
t=5.5\times11=60.5
Question 4
(1 mark)
Here are four numbers
-6 -1 4 7
Select two of these numbers that sum to 1
Answer Type: Multiple Answers
(Order doesn’t matter)
Answer:
-6
7
Question 5
(1 mark)
Here are the first four terms of a number sequence.
2 4 10 28
The rule for continuing this sequence is – multiply the previous term by 3 then subtract 2
Work out the 5th term of this sequence.
Answer Type: Simple Text
Answer: 82
WORKING:
(28\times3)-2=82Question 6
(3 marks)
Below are 6 boxes.

All measurements are in centimetres.
The total length of the 6 boxes is L cm.
In its simplest form, which of the following formulas represents L?
Answer Type: Multiple Choice
Answer: 6x+3
Wrong Answers:
6x+5
5x+3
6x+4
WORKING:
x+1+x+x-1+x+x+x+3 simplifies to 6x+3
Question 7

7(a)
(1 mark)
Which of the following are the correct coordinates for the point A?
Answer Type: Multiple Choice
Answer: (-3, 5)
Wrong Answers:
(5, -3)
(-5, -3)
(3, 5)
7(b)
(1 mark)
Which of the following graphs shows the point B with coordinates (6, 1)?
Answer Type: Multiple Choice
Answer:

Wrong Answers:



7(c)
(1 mark)
Does point B lie on the straight line with equation y=2x-11?
Answer Type: Multiple Choice
Answer: Yes
Wrong Answer: No
WORKING:
If we substitute x=6 and y=1 into the equation y=2x-11,
we get 1=2(6)-11=12-11=1
Hence, the point B lies on the line with equation y=2x-11
7(d)
(1 mark)
Which of the following shows a graph of the line y=3?
Answer Type: Multiple Choice
Answer:

Wrong Answers:

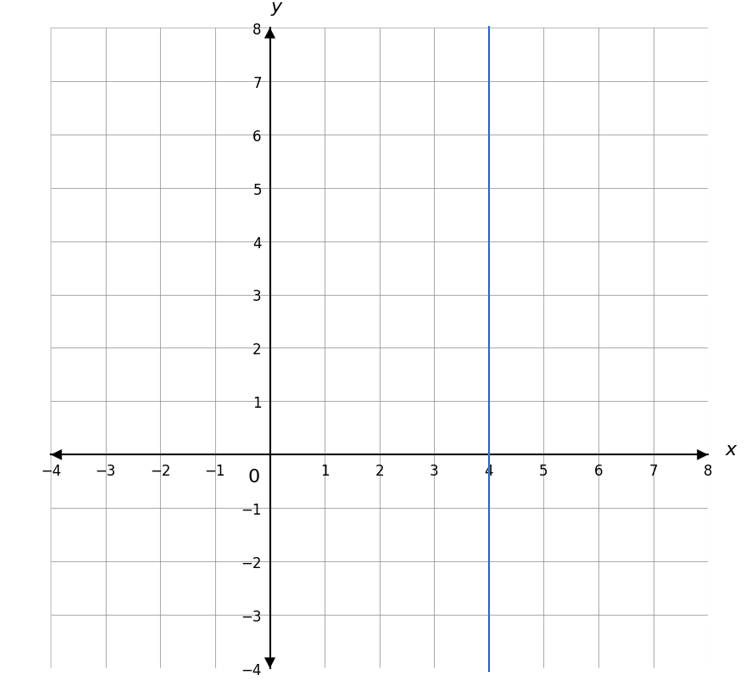

Question 8
(2 marks)
The length of a rectangle is three times as long as the width of the rectangle.
The area of the rectangle is 48 cm^2.
Select which of the following shows the rectangle described above, drawn on a centimetre grid.
Answer Type: Multiple Choice
Answer:

Wrong Answers:



Question 9
(1 mark)
Rey wants to work out 4260\div5
She knows that 4260\div10=426
Rey says that “4260\div5=213, because 10\div5=2 and 426\div2=213”
Is Rey correct in her method of calculating 4260\div5?
Answer Type: Multiple Choice
Answer: No
Wrong Answers: Yes
WORKING:
Rey should have multiplied 426 by 2 instead of dividing by 2
Question 10
Helen and Dominic each threw a dart at a dart board 8 times.
Their scores for each dart is shown below.

10(a)
(1 mark)
Which of the following statements about Helen’s and Dominic’s scores is correct?
Answer Type: Multiple Choice
Answer: Dominic’s scores were more consistent than Helen’s
Wrong Answers:
Helen’s scores were more consistent than Dominic’s
We cannot state whose scores were more consistent based on the information given
WORKING:
As the range of Dominic’s scores is 14, and the range of Helen’s scores is 53, we can see that Dominic’s scores were more consistent.
10(b)
(1 mark)
Helen decides to throw 25 more darts.
The stem and leaf diagram below shows information about the scores she gets.


Calculate the mode of Helen’s scores.
Answer Type: Simple Text
Answer: 5
WORKING:
Reading from the steam and leaf diagram we can see that 5 appears 3 times in the 0 row, more than any other number in a single row.
Hence, 5 is the modal value.
Question 11
There are 50 children going on a school trip.
There must be at least 1 adult for every 6 children.
11(a)
(2 marks)
What is the least number of adults needed for the trip?
Answer Type: Simple text answer
Answer: 9
WORKING:
50\div6=8\frac{1}{3}
So 9 adults are needed.
11(b)
(1 mark)
On the day of the school trip 3 children don’t come as they are unwell.
Does this change the minimum amount of adults needed?
Answer Type: Multiple Choice
Answer: Yes
Wrong Answer: No
WORKING:
(50-3)\div6=7\frac{5}{6}
So only 8 adults are needed now.
Question 12
There are 35 children in a class.
There are 18 girls in the class.
3 of the boys in the class are left handed.
13 of the children who are right handed are girls.
12(a)
(3 marks)
Use this information to work out the values of a, b, c, d and e as shown in the two-way table below.

Answer Type: Multiple Answer
a=5
b=8
c=14
d=27
e=17
WORKING:
a=18-13=5
b=3+5=8
d=35-8=27
c=27-13=14
e=3+14=17
12(b)
(1 mark)
One of the children is chosen at random.
What is the probability that the child chosen is a left-handed girl?
Give your answer as a fraction in its simplest form.
Answer Type: Fraction
Answer: \dfrac{1}{7}
WORKING:
5 girls are left-handed.
So the probability of the child chosen being a left-handed girl is \dfrac{5}{35}=\dfrac{1}{7}
Question 13
(4 marks)
The total surface area of a cube is 486 cm^2.
Work out the volume of the cube.
Answer Type: Simple Text
Answer: 729 cm^3
WORKING:
We know that a cube has 6 faces, so to find the surface area of one face we divide the total surface area by 6,
Area of one face = 486\div6=81 cm^2,
Then to find the length of the cube we take the positive square root of 81,
Length = \sqrt{81}=9 cm
Finally, to work out the volume of the cube we cube 9,
Volume = 9^3= 81 \times 9 = 729 cm^3
Question 14
Here are two fractions.
\dfrac{7}{9} \dfrac{9}{7}
14(a)
(1 marks)
Convert both fractions so they have the same denominator.
Using the common denominator, what fraction is \dfrac{7}{9} equal to?
Answer Type: Fraction
Answer: \dfrac{49}{63}
WORKING:
To find the least common denominator we need to multiply 9 by 7, which gives us 63
63 is the lowest number that both 9 and 7 factorise into.
Then to convert \dfrac{7}{9} into a fraction with 63 as the denominator, we simply multiply the numerator (7) by 7
This gives us the fraction \dfrac{49}{63}
14(b)
(2 mark)
Which fraction is closer to 1?
Answer Type: Multiple Choice
Answer: \dfrac{7}{9}
Wrong Answer: \dfrac{9}{7}
WORKING:
1=\dfrac{63}{63}
\dfrac{7}{9}=\dfrac{49}{63}
\dfrac{9}{7}=\dfrac{81}{63}
We can see that 49 is closer to 63 compared to 81, therefore \dfrac{7}{9} is closer to 1
Question 15
(2 marks)
There are only black, white and blue counters in a bag.
The number of black counters to white counters to blue counters are in the ratio 8:7:10
Work out what percentage of the counters in the bag are black.
Answer Type: Simple Text
Answer: 32\%
WORKING:
There are 8+7+10=25 counters in the bag.
8 out of 25 counters are black.
\dfrac{8}{25}\times 100=32 \%
Question 16
Brian wants to buy 28 boxes of chocolate.
Each box of chocolate costs £3.70
Brian works out that 30\times4=120 to estimate the cost of 28 boxes of chocolate.
16(a)
(1 mark)
Has Brian underestimated or overestimated the cost of 28 boxes of chocolate?
Answer Type: Multiple Choice
Answer: Overestimate
Wrong Answer: Underestimate
WORKING:
Brian has rounded both 28 and £3.70 up to 30 and £4 respectively.
Therefore his estimate is an overestimate.
16(b)
(4 marks)
There is a special offer.

Work out the actual cost of buying 28 boxes of chocolate using the offer above.
Answer Type: Simple Text
Answer: £88.06
WORKING:
We need to first calculate the total cost without the offer:
28\times£3.70=(28\times£3)+(28\times£0.70)=£84+£19.6=£103.60
10% of £103.60 is £10.36
5% of £103.6 is £5.18
So 15% of £103.6 is £10.36+£5.18=£15.54
Actual cost of buying 28 boxes = £103.6-£15.54=£88.06
Question 17
(2 marks)
Liam has written down the numbers 4, 5 and 6 on separate pieces of paper, folds them up and puts them in a bag.
He does the same for a second bag, but this time her writes the numbers 1, 4 and 8
If Liam takes a random piece of paper from each bag, what is the probability that the total score is an even number?
Give your answer as a fraction in its simplest form.
Answer Type: Fraction
Answer: \dfrac{5}{9}
WORKING:
The possible values Liam can get when adding the two numbers together are:
5 8 12 6 9 13 7 10 14
So 5 out of a possible 9 values are even.
Hence, the probability that the total score is even is \dfrac{5}{9}
Question 18
(2 marks)
Vanessa, Heather and Kyle share £360 in the ratio 5:3:4
How much does Heather get?
Answer Type: Simple Text
Answer: £90
WORKING:
£360\div(5+3+4)=£30
£30\times3=£90
Question 19
(3 marks)
Here is the list of ingredients for making 12 brownies.

Sam wants to make 18 brownies.
Work out how much of each of the ingredients he needs.
Answer Type: Multiple Answer
Answer:
165 g butter
270 g sugar
45 g cocoa powder
90 g self raising flour
3 eggs
WORKING:
We need the ingredients for 6 more brownies.
6 is 50\% of 12, so we need to increase the ingredients by 50\%
Butter: 110+50\%=110+55=165 g
Sugar: 180+50\%=180+90=270 g
Cocoa powder: 30+50\%=30+15=45 g
Self-raising flour: 60+50\%=60+30=90 g
Eggs: 2+50\%=2+1=3
Question 20
(3 marks)
Jessica and Dan use a calculator to work out:
\dfrac{408}{2.95^2+8.8}
Jessica’s answer is 23.31095558
Dan’s answer is 233.1095558
One of these answers is correct.
By using approximations, who is correct?
Answer Type: Multiple Choice
Answer: Jessica
Wrong Answer: Dan
WORKING:
\dfrac{408}{2.95^2+8.8}\approx \dfrac{400}{3^2+9}=\dfrac{400}{18}\approx \dfrac{400}{20}=20
We can see that the approximation 20 is much closer to Jessica’s answer compared to Dan’s.
Question 21
(3 marks)
\dfrac{0.0009\times0.04}{0.1}
Which of the following represents the fraction above in standard form?
Answer Type: Multiple Choice
Answer: 3.6\times10^{-4}
Wrong Answers:
0.36\times10^{-3}
3.6\times10^{-5}
36\times10^{-5}
WORKING:
0.0009\times0.04=0.000036
0.000036\div0.1=0.000036\times10=0.00036
0.00036=3.6\times10^{-4}
Question 22
22(a)
(2 marks)
Work out \,\,\dfrac{1}{3}+\dfrac{3}{7}
Give your answer as a fraction in its simplest form.
Answer Type: Fraction
Answer: \dfrac{16}{21}
WORKING:
\dfrac{1}{3}+\dfrac{3}{7}
=\dfrac{1}{3}\times\dfrac{7}{7}+\dfrac{3}{7}\times\dfrac{3}{3}
=\dfrac{7}{21}+\dfrac{9}{21}
=\dfrac{16}{21}
22(b)
(1 mark)
What is the value of \,\,3^{-4}?
Give your answer as a fraction in its simplest form.
Answer Type: Fraction
Answer: \dfrac{1}{81}
WORKING:
3^{-4}=\dfrac{1}{3^4}=\dfrac{1}{81}Question 23
(2 marks)
Write 96 as a product of its prime factors.
ANSWER: Multiple Choice
A: 2^5\times 3
B: 2^4\times 3
C: 3^5\times 2
D: 3^4\times 2
Answer: A
Workings:

Question 24
(4 marks)
Alice is 4 years older than Bob.
Claire is twice as old as Alice.
The sum of their three ages is 48
Find the ratio of Bob’s age to Alice’s age to Claire’s age.
Answer: Multiple Choice
A: 9:13:26
B: 8:16:32
C: 12:18:36
D: 7:14:28
Answer: A
Workings:
Represent Alice as A, Bob as B and Claire as C.
A - 4 = B
C = 2A
A + B + C = 48
Substitute the first two equations in to the third to get it in terms of A.
2A + A - 4 + A = 48
4A - 4 = 48
A = \dfrac{52}{4} = 13
The value for A can then be substituted into the first two equations to find B and C.
A - 4 = 13 - 4 = 9 = B
2A = 2\times 13 = 26 = C
Therefore the ratio of Bob’s age to Alice’s age to Claire’s age can be written as: \,\,\,9:13:26
Question 25
(4 marks)

ABCD is a parallelogram.
CBF is a straight line.
DEF is a straight line that intersects with AB at point E.
Angle BEF = 27\degree
Angle ABC = 82\degree
Calculate the angle ADE.
ANSWER: Simple text answer
Answer: 55 \degree
Workings:
Adjacent angles in a Parallelogram add up to 180, so DAE = 180\degree - ABC = 180\degree - 82 = 98\degree
Angles AED and BEF are vertically opposite and therefore identical, so AED = BEF = 27\degree
Angles in a triangle add up to 180\degree, so 98\degree+27\degree + ADE = 180\degree
ADE = 180\degree - 98\degree - 27\degree = 55\degreeQuestion 26
(4 marks)
The diagram shows a circular badge containing another circle within.
Both circles have the same centre, O.
The inner circle is split into two sections horizontally along its centre.

Calculate the shaded area of the badge in terms of \pi
ANSWER: Multiple Choice
A: 32\pi cm^2
B: 24\pi cm^2
C: 28\pi cm^2
D: 28\pi cm^2
Answer: A
Workings:
The diameter of the larger circle is 24 cm.
Because there is 4 cm between the circumferences of the two circles, the diameter of the smaller circle must be: 24 - 8 = 16 cm.
The radius of the smaller circle is half its diameter: \dfrac{16}{2} = 8 cm.
Calculate the area of the smaller circle as: \pi \times r^2 = \pi \times 8^2 = 64\pi
The area of the shaded sector is half the area of the smaller circle:
Shaded area = \dfrac{64\pi}{2} = 32\pi cm^2
Question 27
The table shows information about the annual earnings of 30 people who work in an office.

27(a)
(3 marks)
Work out an estimate for the mean of the annual earnings.
ANSWER: Simple Text
Answer: £19600
Workings:
First find the midpoint of the annual earnings for each row.
Multiply the midpoint by the frequency for each row.
The first two steps can be shown in the below table:

Sum all the values for midpoint \times frequency to get:
48000 + 162000 + 220000 + 110000 + 48000 = 588000
Divide this sum by the total frequency to get the mean of the annual earnings:
\dfrac{588000}{30} = £19600
We can calculate this division using the bus stop method, with 588 \div 3 and then adding the required number of zeros:

588 \div 3 = 196\, so 588000 \div 30 = 19600
27(b)
(1 mark)
Which of the following is a reason why the mean might not be the best way to represent the average of this data?
ANSWER: Multiple Choice
A: Outliers will affect the mean value.
B: It takes too long to calculate.
C: It is not possible to calculate the mean using inequalities.
D: The mean gives the most popular value, which there may be more than one of.
Answer: A
Workings:
The mean uses outliers in the data which may give an inaccurate representation of the average.
Question 28
(4 marks)
The area of this rectangle is 64 cm^2

Find the value of x.
ANSWER: Simple Text Answer
Answer: 4 cm
Workings:
4y-4 = 2y+6
2y=10
y=5
Area of rectangle is given by:
(4y-4)x=64
Substitute in y=5:
(20-4)x=64
16x=64
x=4
Question 29
Which of the following is the correct graph for y = x^2+2?
ANSWER: Multiple Choice
Answer:

Wrong Answers:

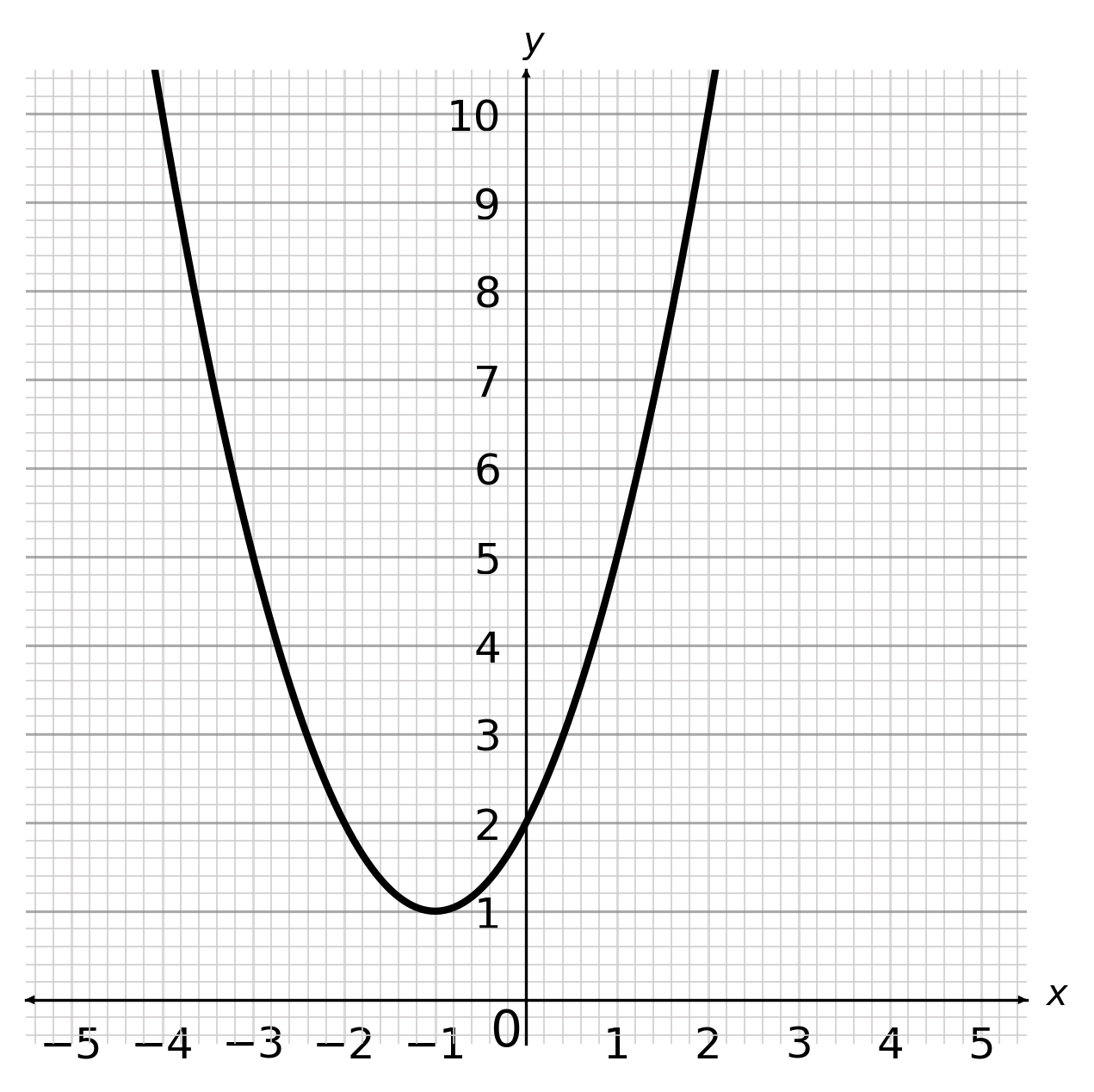

Workings:
The graph of y = x^2 + 2 gives a parabola where it reaches the minimum point when x=0 and y=2
Question 30
(2 marks)
A t-shirt is reduced by 20\%
The sale price of the t-shirt is £8.60
Work out the original price of the t-shirt.
Answer type: Simple Text
Answer:£10.75
WORKING:
First we need to covert 20\% into a fraction,
20\% =\dfrac{1}{5}
So we can see that £8.60 is \dfrac{4}{5} of the original price.
Original price \times\dfrac{4}{5}=£8.60
Original price =£8.60\div\dfrac{4}{5}=£8.60\times\dfrac{5}{4}
Original price =\dfrac{£8.60\times5}{4}=\dfrac{£43}{4}=£10.75
