NOTE: Q16-23 are the same as Q1-8 on Nov 17 Higher Paper 2
(DOESN’T NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1 [1 mark]
What is \dfrac{9}{100} as a decimal?
Answer type: Simple text answer
ANSWER: 0.09
Question 2 [1 mark]
Write down a multiple of 8 that is between 90 and 100
Answer type: Simple text answer
ANSWER: 96
Question 3
Simplify the following expressions.
Question 3(a) [1 mark]
2p \times 7q
Answer type: Multiple choice type 1
A: 14pq
B: 14p + q
C: 14 + p + q
D: 14 + pq
ANSWER: A
Question 3(b) [1 mark]
r \times r \times 2
Answer type: Multiple choice type 1
A: 2r^2
B: 2r
C: 4r
D: r^2 + 2
ANSWER: A
Question 3(c) [1 mark]
\dfrac{5m + 4m}{3}
Answer type: Multiple choice type 1
A: 3m
B: 9m
C: \dfrac{20m}{3}
D: \dfrac{3}{m}
ANSWER: A
Question 4
Jarvis buys some tinned food.
He buys soup, beans, tuna and corned beef.
Jarvis buys
3 tins of soup weighing 400 g each
4 tins of beans weighing 425 g each
2 tins of tuna weighing 150 g each
Each tin of corned beef weighs 335 g
The tins have a total weight of 4.205 kg.
Question 4(a) [3 marks]
How many tins of corned beef does Jarvis buy?
Answer type: Simple text answer
ANSWER: 3
WORKING:
3s = 3 \times 400 = 1200 g
4b = 4 \times 425 = 1700 g
2t = 2 \times 150 = 300 g
Total weight = 4205 g
Weight of corned beef = 4205 - 1200 - 1700 - 300 = 1005 g
Number of tins of corned beef = 1005 \div 335 = 3
Question 4(b) [2 marks]
Gemma wants to buy 7 tins of sweetcorn.
She asks for 1 kg of sweetcorn at the shop.
She assumes that each tin of sweetcorn has a weight of 150 g
If Gemma’s assumption is correct, will she get 7 tins of sweetcorn?
Multiple choice type 1
A: Yes
B: No
ANSWER: B
WORKING:
7 \times 150 = 1050 g =1.05 kg
1.05 kg is greater than 1 kg so she will not get 7 tins
Question 4(c) [1 mark]
If Gemma’s assumption is not correct, what weight would the tins of sweetcorn need to be so she could get 7 tins of sweetcorn?
Give your answer rounded down to the nearest gram.
Answer type: Simple text answer
ANSWER: 142 g
WORKING:
1000 \div 7 = 142 g (rounded down to nearest g)
Question 5 – here
80 people were asked to name their favourite cuisine.
The table below shows the results.

Question 5(a) [2 marks]
What fraction of the 80 people asked did not choose Italian as their favourite cuisine?
Give your answer in its simplest form.
Answer type: Fraction
ANSWER: \dfrac{11}{20}
WORKING:
80 - 36 = 44 people did not choose Italian
\dfrac{44}{80} = \dfrac{11}{20} as a fraction
Question 5(b) [4 marks]

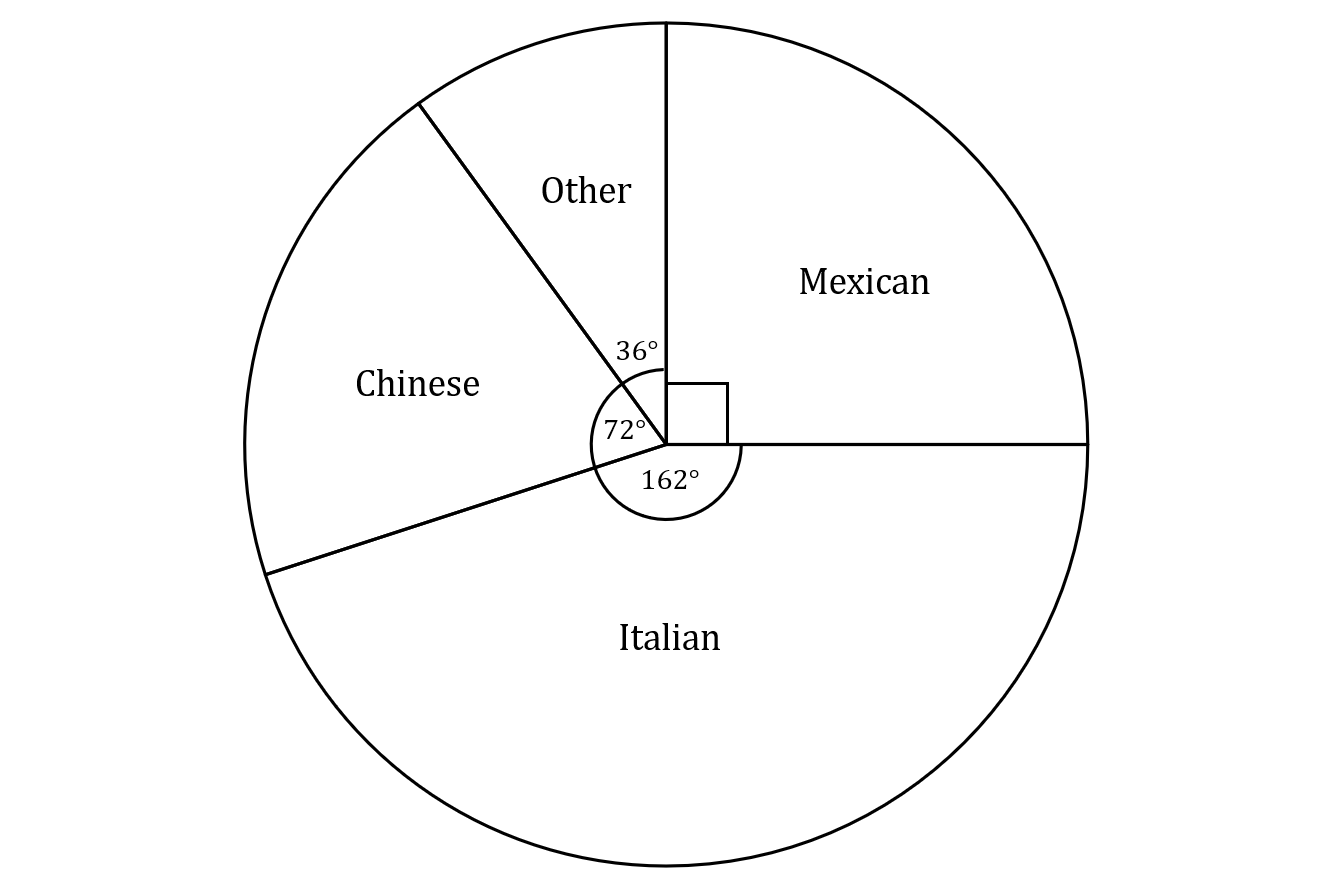
Which of the following is the correct completion of the pie chart above?
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: A
WORKING:
We need to calculate the angles corresponding to each remaining category:
Italian: angle = \dfrac{36}{80} \times 360 = 162 \degree
Chinese: angle = \dfrac{16}{80} \times 360 = 72 \degree
Other: angle = \dfrac{8}{80} \times 360 = 36 \degree
The pie chart look as follows:
Question 6
Question 6(a) [1 mark]
Ronald and Terry share some food in the ratio 3:2
What fraction of the food does Ronald get?
Answer type: Fraction
ANSWER: \dfrac{3}{5}
WORKING:
\dfrac{3}{3+2} = \dfrac{3}{5}
Question 6(b) [1 mark]
Sarah and Liz share some money.
Liz gets \dfrac{1}{5} of the money.
What is the ratio of the amount of money Sarah gets to the amount of money Liz gets?
Answer type: Multiple choice type 1
A: 4:1
B: 1:4
C: 5:1
D: 1:5
ANSWER: A
WORKING:
Sarah : Liz = \dfrac{4}{5} : \dfrac{1}{5} = 4:1
Question 7 [2 marks]
Josh says,
“There are more prime numbers between 0 and 10 than there are between 10 and 20”
Is Josh right?
Choose the correct statement.
Answer type: Multiple choice type 1
A: Yes, there are more prime numbers between 0 and 10 than there are between 10 and 20
B: No, there are less prime numbers between 0 and 10 than there are between 10 and 20
C: No, there is the same number of prime numbers between 0 and 10 than there are between 10 and 20
ANSWER: C
WORKING:
Primes between 0 and 10: \,\,\,\,\,\,2,3,5,7
Primes between 10 and 20: \,\,\,\,\,\,11,13,17,19
There are the same number of primes between 0 and 10 than there are between 10 and 20
Question 8
Nick drew the graph below to show the percentage of a stadium’s capacity used for six months.

Question 8(a) [1 mark]
What is wrong with the graph?
Answer type: Multiple choice type 1
A: The vertical scale is not linear
B: The horizontal scale is not numerical
C: The points are plotted incorrectly
D: The axis titles are wrong
ANSWER: A
WORKING:
40 is missing on the vertical axis (y-axis)
Question 8(b) [1 mark]
What best describes the trend in the percentage of a stadium’s capacity used?
Answer type: Multiple choice type 1
A: There is a negative trend
B: There is a positive trend
C: There is no trend
ANSWER: A
Question 9 – here
Here is a map of an island.

A straight road joins Buckshire and St. Peters, perpendicular to the straight road joining Buckshire and Hiloway.
A straight road joins St. Peters and Hiloway.
Question 9(a) [2 marks]
Using the information given on the map, calculate the real distance between St. Peters and Hiloway.
Answer type: Simple text answer
ANSWER: 100 km
WORKING:
Distance between Buckshire and St. Peters = 6 \times 10 = 60 km
Distance between Buckshire and Hiloway = 8 \times 10 = 80 km
Using Pythagoras,
Distance between St. Peters and Hiloway =\sqrt{60^2 + 80^2} = 100 km
Question 9(b) [1 mark]
Find the bearing of Hiloway from St. Peters.
Answer type: Simple text answer
ANSWER: 115 \degree
WORKING:
Bearing = 180 - 65 = 115 \degree
Question 10
The diagram shows two shapes drawn on a centimetre grid.

Question 10(a) [2 marks]
Calculate the area of shape A
Answer type: Simple text answer
ANSWER: 30 cm^2
WORKING:
Area = b \times h = 5 \times 6 = 30 cm^2
Question 10(b) [1 mark]
What is the mathematical name of triangle B?
Answer type: Multiple choice type 1
A: Isosceles triangle
B: Scalene triangle
C: Equilateral triangle
D: Right-angled triangle
ANSWER: A
Question 11 [3 marks] – here
The table below shows a cricket club’s income in June from membership fees, club hire and a charity event.

Choose the ratio that expresses
the income from membership fees to the income from club hire to the income from the charity event
in its simplest form.
Answer type: Multiple choice type 1
A: 7:2:1
B: 35 : 10 : 5
C: 175:50:21
D: 1750:500:250
ANSWER: A
WORKING:
Membership fees = 35 \times £50 = £1750
Club hire = £500
Charity event = (42 \times £5) + £40 = £210 + £40 = £250
Membership fees : club hire : charity event = 1750 : 500 : 250
If we divide each part of the ratio by 250, we get 7:2:1 as its simplest form
Question 12
300 people live in a village.
46 people do not own a car.
13 males do not own a car.
161 people are male.
Question 12(a) [3 marks]
Use this information to complete the frequency tree below, by finding the values of a,b,c,d,e and f

Answer type: Multiple answers type 1
ANSWERS:
a = 254
b = 46
c = 148
d = 106
e = 13
f = 33
WORKING:
46 do not own a car
300 - 46 = 254 own a car
13 males do not own a car
46 - 13 = 33 females do not own a car
161-13 = 148 males own a car
254 - 148 = 106 females own a car
The frequency tree can then be filled in as follows:

Question 12(b) [2 marks]
One of the people who own a car is chosen at random.
What is the probability that this person is male?
Give your answer as a decimal to 3 decimal places.
Answer type: Fraction
ANSWER: 0.583
WORKING:
254 people own a car, of which 148 are male.
Probability = \dfrac{148}{254} = 0.583 (3 dp)
Question 13 [3 marks]
Nancy makes socks in a factory.
She is paid 62p for each pair of socks she makes.
Rod works in a supermarket.
He works 40 hours and makes £344
How many pairs of socks does Nancy need to make in one hour in order to be on a higher hourly rate of pay than Rod?
Answer type: Simple text answer
ANSWER:
WORKING:
Rod’s hourly pay = £344 \div 40 = £8.60
8.60 \div 0.62 = 13.87...
So, Nancy needs to make at least 14 pairs of socks in one hour in order to be on a higher hourly rate of pay than Rod.
Question 14
a and b are positive integers.
Question 14(a) [2 marks]
Given that a and b are positive integers less than 5,
find the values of a and b such that 6(a+b) is a multiple of 7
Answer type: Multiple answers type 2 (can be wither way round)
ANSWERS:
a = 3
b = 4
WORKING:
6(3+4) = 6(7) = 42 which is a multiple of 7
There are no other numbers less than 5 that add together to make 7
So, a = 3 and b = 4\,\,\,\,\,\, or \,\,\,\,\,\,a = 4 and b = 3
Question 14(b) [2 marks]
c and d are odd positive integers.
Frankie says
“6(c+d) will always be a multiple of 12”
Is she correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: A
WORKING:
Since c and d are odd, let c = 2n+1 and d = 2m+1
where n and m are positive integers.
Then,
6(c+d) = 6((2n+1) + (2m+1)) = 6(2n+2m+2) = 12(n+m+1)
Since n and m are positive integers, n+m+1 is a positive integer.
Hence 12(n+m+1) is a multiple of 12
Therefore 6(c+d) is always a multiple of 12, so Frankie is correct.
Question 15
Mr Jordan uses fuel in his car.
At the beginning of August there were 20 litres of fuel in his fuel tank.
Mr Jordan bought enough fuel to fill the tank completely.
He paid £1.20 per litre for this fuel.
He paid a total amount of £48
At the end of October Mr Jordan had 10 litres of fuel in the tank.
He bought enough fuel to fill the tank completely.
The cost of fuel had increased by 5\%
Calculate the total amount Mr Jordan paid for the fuel he bought in October.
Answer type: Simple text answer
ANSWER: £63
WORKING:
August:
48 \div 1.20= 40 litres
Total = 20 + 40 = 60 litres
October:
x + 10 = 60
x = 50 litres
New price per litre = £1.20 \times 1.05 = £1.26
Total price paid = £1.26 \times 50 = £63
Question 16
Solve 4(x+4) = 2(3x+1)
ANSWER: Simple Answer
Answer: x=7
Workings:
Expanding the brackets:
4x+16 = 6x+2
2x=14
x=7
Marks = 3
Question 17
Mark buys 50 packs of Toilet Roll for \pounds 120.00 total.
He then sells the packs individually at \pounds 2.90 each.
Calculate the percentage profit that Mark makes to 1 decimal place.
ANSWER: Simple Answer
Answer: 20.8 %
Workings:
Calculate the total sale price for all 50 packs of toilet roll:
50\times \pounds 2.90 = \pounds 145
Divide this value by the original purchase price of all the toilet rolls and multiply by 100 to get the percentage of the original amount:
\dfrac{145}{120} = 120.8\%
So the percentage profit is 120.8-100=20.8\%
Question 18
Suraj walks around a circle, starting at point A and making a complete cycle through all six points, which are equally spaced apart.

The distance between points A and B is 15 metres.
Calculate the radius of the circle to 1 decimal place.
ANSWER: Simple Answer
Answer: 14.3 metres
Workings:
Calculate the circumference of the circle:
15\times 6 = 90 metres
Use the formula:
\text{circumference} = \pi \times \text{diameter}
to find the diameter.
\text{diameter} = \dfrac{\text{circumference}}{\pi} = \dfrac{90}{\pi} = 28.648 metres
\text{radius} = \dfrac{\text{diameter}}{2} = \dfrac{28.648}{2} = 14.3 metres to 1 dp.
Marks = 3
Question 19
There are a number of coloured fish in a pond.
The fish are either Yellow, Red or Blue.
There are three times as many Yellow fish as Red fish.
There are six times as many Blue fish as Yellow fish.
Elliot catches a random fish from the pond before putting it back.
What’s the probability that Elliot catches a Red fish?
ANSWER: Fraction
Answer: \dfrac{1}{22}
Working:
The two statements can be written as equations:
Y = 3R\\
B=6Y
This can then be written as a ratio in the form Yellow : Red : Blue
3 : 1 : 18
This gives a probability of \dfrac{1}{3+1+18} = \dfrac{1}{22} of Elliot catching a Red fish.
Marks = 3
Question 20
The diagram below shows shape A on a graph.

Which shape on the diagram below shows A having been rotated 180\degree around point (1,1)?

ANSWER: Multiple Choice
A: Shape P
B: Shape Q
C: Shape R
D: Shape S
Answer: C
Workings:
Using the bottom left corner of the triangle as a focus point, it is 1 space to the right and 3 above the centre of rotation.
Because the shape is being rotated 180\degree the new shape will have this point 1 to the left and 3 below.
It is then possible to find the other two points the same way, to give Shape R as the correct shape.
Marks = 2
Question 21
21(a):
\dfrac{a^7}{a^x} = a^5
Find the value of x.
ANSWER: Simple Answer
Answer: x = 2
Workings:
\dfrac{a^7}{a^x} = a^{7-x} = a^5
7-x = 5
x = 2
Marks = 1
21(b)
(b^y)^2 = b^8
Find the value of y.
ANSWER: Simple Answer
Answer: y = 4
Workings:
(b^y)^2 = b^{2y} = b^8
2y = 8
y = 4
Marks = 1
21(c):
1000^y \times 100^{2y} = 10^{35}
Find the value of y.
ANSWER: Simple Text Answer
Answer: y = 5
Workings:
1000^y = (10^3)^y = 10^{3y}
100^{2y} = (10^2)^{2y} = 10^{4y}
1000^y \times 100^{2y} = 10^{3y} \times 10^{4y} = 10^{35}
3y + 4y = 7y = 35
y = 5
Marks = 2
Question 22
The diagram below, ABCD, represents a trapezium.

Find the angle BCD, giving your answer to 1 decimal place.
ANSWER: Simple Answer
Answer: 138.5\degree
Workings:
Call the section of side AB that is adjacent to AD and the 6 cm side: side x
To find x, use Pythagoras
\sqrt{11^2 - 6^2} = \sqrt{85}
To calculate the section at the other end of AB:
45 - \sqrt{85} - 29 = 6.78 cm
To find the angle CB makes with the perpendicular:
\tan^{-1}(\dfrac{6.78}{6}) = 48.493\degree
Add 90 to this to get the full angle BCD
90 + 48.493 = 138.5\degree to 1 dp.
Marks = 5
Question 23
23(a):
Using a calculator, work out \dfrac{\cos(40\degree) + \cos(20\degree)}{\sin(40\degree) - \sin(20\degree)}
Write down all figures on the calculator display.
ANSWER: Simple Answer
Answer: 5.67128182
Marks = 2
23(b):
Type your answer to part (a) to 2 decimal places.
ANSWER: Simple Answer
Answer: 5.67
Marks = 1
Question 24
Question 24(a) [2 marks]
Solve 3x^2 = 48
Answer type: Multiple answers type 2 (can be either way round)
ANSWERS:
x = 4
x = -4
WORKING:
3x^2 = 48
x^2 = 16
x = \pm 4
Question 24(b) [2 marks]
Expand and simplify (3x+1)(2x-3)
Answer type: Multiple choice type 1
A: 6x^2 - 7x - 3
B: 6x^2 + 7x - 3
C: 6x^2 + 11x + 3
D: 6x^2 - 11x + 3
ANSWER: A
WORKING:
(3x+1)(2x-2)
= 6x^2 - 9x + 2x - 3
= 6x^2 - 7x - 3
Question 24(c) [1 mark]
Choose the correct factorisation of x^2 + 8x + 16
Answer type: Multiple choice type 1
A: (x+4)^2
B: (x+2)^2
C: (x+4)(x-4)
D: (x+2)(x-2)
ANSWER: A
WORKING:
x^2 + 8x + 16 = (x+4)^2