NOTE: Q1-6 are the same as Q21-26 on June 17 Foundation Paper 1
(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1
The scatter graph shows the maximum temperature and the number of hours of sunshine in fourteen German Cities on one day.

Question 1(a) [1 mark]
One of the points is an outlier.
What are the coordinates of this point?
Answer type: Multiple choice type 1
A: (10, 18)
B: (15, 20)
C: (18, 10)
D: (20, 15)
Answer type: Simple text answer
ANSWER: A
Question 1(b) [1 mark]
For all the other points, what is the type of correlation?
Answer type: Multiple choice type 1
A: Positive correlation
B: Negative correlation
C: No correlation
ANSWER: A
Question 1(c) [2 marks]
On the same day, in another German City, the maximum temperature was 17.2 \degree C.
Choose the closest estimate for the number of hours of sunshine in this City on this day.
Answer type: Multiple choice type 1
A: 13 hours
B: 15 hours
C: 11 hours
D: 18 hours
ANSWER: A
Question 1(d) [1 mark]
A weatherman says,
“Temperatures are higher on days when there is more sunshine.”
Does the scatter graph support what the weatherman says?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: A
WORKING:
Yes, as the majority of points for high temperatures appear when there are more hours of sunshine (i.e. there is a positive correlation)
Question 2 [2 marks]
Express 48 as the product of its prime factors in index form.
Choose the correct expression.
Answer type: Multiple choice type 1
A: 2^4 \times 3
B: 2^3 \times 3
C: 2^3 \times 3^2
D: 2 \times 3^3
ANSWER: A
WORKING:
Use a prime factor tree:

48 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3
Question 3 [3 marks]
Work out 46.3 \times 5.2
Answer type: Simple text answer
ANSWER: 240.76
WORKING:
Move the decimal places on each number, to make them easier to use to calculate.

20000 + 3000 + 150 = 23150
800 + 120 + 6 = 926
23150 + 926 = 24076
Now move the decimal place back, to get 240.76
Question 4 [3 marks]

The area of the square ABCD is 12 cm^2.
What is the correct equation formed from this information?
Answer type: Multiple choice type 1
A: x^2 + 4x = 8
B: x^2 + 2x = 8
C: x^2 + 4x = 12
D: x^2 + 4x = 4
ANSWER: A
WORKING:
(x+2)^2 = 12
x^2 + 4x + 4 = 12
x^2 + 4x = 8
Question 5 [5 marks]
A rectangular frame is made from 5 straight pieces of metal, as seen below.

The mass of the metal is 2.5 kg per metre.
What is the total mass of the metal in this frame?
Answer type: Simple text answer
ANSWER: 95 kg
WOKRING:
Calculate the length of the diagonal by using Pythagoras’ theorem:
\sqrt{6^2 + 8^2} = \sqrt{100} = 10 m
Add together the lengths of all five pieces of metal:
6+6+8+8+10 = 38 m
Multiply this by 2.5 kg to calculate the total mass of the frame:
38 \times 2.5 = 95 kg
Question 6 [2 marks]
The equation of line A is y = 4x - 1
The equation of line B is 2y - 8x - 9 = 0
Are these two lines parallel, perpendicular or neither?
Answer type: Multiple choice type 1
A: Parallel
B: Perpendicular
C: Neither
ANSWER: A
WORKING:
Rearrange the equation of line B:
2y - 8x - 9 = 0
2y = 8x + 9
y = 4x + \dfrac{9}{2}
Line A and Line B have the same gradient, so are parallel.
Question 7 [3 marks]
There are 20 boys and 10 girls in a class.
The class has a test.
The mean mark for all the class is 80
The mean mark for the girls is 60
Work out the mean mark for the boys.
Answer type: Simple text answer
ANSWER: 90
WORKING:
80 \times 30 = 2400
60 \times 10 = 600
2400 - 600 = 1800
Mean mark for the boys is
1800 \div 20 = 90
Question 8
Question 8(a) [1 mark]
What is 6.34 \times 10^{-4} as an ordinary number?
Answer type: Simple text answer
ANSWER: 0.000634
Question 8(b) [2 marks]
Calculate (5.6 \times 10^3) \div (7 \times 10^{-2})
Choose the correct answer.
Answer type: Multiple choice type 1
A: 8 \times 10^4
B: 3.92 \times 10^2
C: 8 \times 10^5
D: 3.92 \times 10^3
ANSWER: A
WORKING:
5.6 \div 7 = 0.8
10^3 \div 10^{-2} = 10^{3-(-2)} = 10^5
0.8 \times 10^5 = 8 \times 10^4
Question 9 [2 marks]
Damien buys a fridge.
20 \% VAT is added to the price of the fridge.
Damien then has to pay a total of £900
What is the price of the fridge with no VAT added?
Answer type: Simple text answer
ANSWER: £750
WORKING:
£900 \div 1.2 = £750
Question 10 [3 marks]
x(x+1)(x+2) can be written in the form ax^3 + bx^2 + cx, where a, b and c are positive integers.
What are the values of a, b and c?
Answer type: Multiple answers type 1
ANSWER:
a = 1
b = 3
c = 2
WORKING:
x(x+1)(x+2)
x(x^2 + 2x + x + 2)
x(x^2 + 3x + 2)
x^3 + 3x^2 + 2x
Question 11
The graph of y=f(x) is drawn on the grid.

Question 11(a)
What are the coordinates of the turning point of the graph?
Answer type: Multiple choice type 1
A: (1.5, -0.25)
B: (1.5, 0.5)
C: (1, 0)
D: (2, 0)
ANSWER: A
WORKING:
The turning point of the graph is the point where the gradient is 0
Question 11(b)
What are the roots of f(x)=0?
Answer type: Multiple answers type 2
ANSWER:
x = 1
x = 2
WORKING:
The roots of f(x)=0 are the x values of the points where the graph crosses the x axis
Question 11(c)
Use the graph to find f(3)
Answer type: Simple text answer
ANSWER: 2
WORKING:
Go up from 3 on the x axis until you meet the graph.
Go across until you meet the y axis, which is at 2
Question 12
Question 12(a)
What is the value of 36^{-\frac{1}{2}}?
Answer type: Multiple choice type 1
A: \dfrac{1}{6}
B: 6
C: \dfrac{1}{36}
D: 3
ANSWER: A
WORKING:
36^{-\frac{1}{2}} = \dfrac{1}{\sqrt{36}} = \dfrac{1}{6}
Question 12(b)
Find the value of \bigg( \dfrac{125}{27} \bigg)^{\frac{2}{3}}
Answer type: Fraction
ANSWER: \dfrac{25}{9}
WORKING:
\bigg( \dfrac{125}{27} \bigg) ^{\frac{2}{3}}
=\bigg( \bigg( \dfrac{125}{27} \bigg)^{\frac{1}{3}} \bigg)^2
=\bigg( \dfrac{125^{\frac{1}{3}}}{27^{\frac{1}{3}}} \bigg)^2
=\bigg( \dfrac{5}{3} \bigg)^2
=\bigg( \dfrac{25}{9} \bigg)
Question 13
The table below shows a set of values for x and y.

y is inversely proportional to the square of x.
Question 13(a) [2 marks]
What is the equation for y in terms of x?
Answer type: Multiple choice type 1
A: y = \dfrac{36}{x^2}
B: y = \dfrac{6}{x^2}
C: y = 36x^2
D: y = 18x^2
ANSWER: A
WORKING:
y \propto \dfrac{k}{x^2}
y = \dfrac{k}{x^2}
Substitute in x=1 and y=36 to find k
36 = \dfrac{k}{1^2}
k = 36
Therefore the equation for y in terms of x is y = \dfrac{36}{x^2}
Question 13(b) [2 marks]
Find the positive value of x when y = 25
Answer type: Fraction
ANSWER: \dfrac{6}{5}
WORKING:
y = \dfrac{36}{x^2}Rearrange to get
x^2 = \dfrac{36}{y}
x = \pm \sqrt{\dfrac{36}{y}}
We only want the positive value of x, when y=25, so we get
x = \sqrt{\dfrac{36}{25}} = \dfrac{6}{5}
Question 14 [4 marks]
White shapes and black shapes are used in a game.
Some of the shapes are circles.
All the other shapes are triangles.
The ratio of the number of white shapes to the number of black shapes is 7:3
The ratio of the number of white circles to the number of white triangles is 1:2
The ratio of the number of black circles to the number of black triangles is 3:1
Work out what fraction of all the shapes are circles.
Answer type: Fraction
ANSWER: \dfrac{11}{24}
WORKING:
The ratio of white to black shapes is 7:3, so \dfrac{3}{10} of the shapes are black.
The ratio of white circles to white triangles is 1:2, so \dfrac{1}{3} of the white shapes are circles.
The ratio of black circles to black triangles is 3:1, so \dfrac{3}{4} of the black shapes are circles.
Therefore, the fraction of all the shapes that are circles is
\bigg(\dfrac{7}{10} \times \dfrac{1}{3} \bigg) + \bigg(\dfrac{3}{10} \times \dfrac{3}{4} \bigg) = \dfrac{7}{30} + \dfrac{9}{40} = \dfrac{28}{120} + \dfrac{27}{120} = \dfrac{55}{120} = \dfrac{11}{24}
Question 15
A cone has a volume of 48 cm^3
The radius of the cone is 5.22 cm.
The equation for the volume of a cone is V = \dfrac{1}{3} \pi r^2 h
Question 15(a) [3 marks]
Work out an estimate for the height of the cone.
Answer type: Multiple choice type 1
A: 2 cm
B: 4 cm
C: 3 cm
D: 5 cm
ANSWER: A
WORKING:
Using approximate values
50 = \dfrac{1}{3} \times 3 \times 5^2 \times h
50= 25h
h = 2 cm
Question 15(b) [1 mark]
Russ uses a calculator to work out the height of the cone to 2 decimal places.
Will your estimate be more than John’s answer or less than John’s answer?
Answer type: Multiple choice type 1
A: More
B: Less
ANSWER: A
Question 16
Question 16(a) [2 marks]
Is the sum of two consecutive numbers is odd or even?
Answer type: Multiple choice type 1
A: Odd
B: Even
ANSWER: A
Question 16(b) [2 marks]
The following lines of working show the proof for part (a)
Line 1: If a number is n, then the next number is n+1
Line 2: The sum is therefore n+n+1=2n+1
Line 3:
What is the missing line (Line 3) from the above working?
Answer type: Multiple choice type 1
A: 2n is even, so 2n+1 must be odd
B: 2n is odd, so 2n+1 must be even
C: 2n is even, so 2n+1 must be even
D: 2n=0 , so 2n+1 must be odd
ANSWER: A
WORKING:
If a number is n, then the next number is n+1
The sum is therefore n+n+1 = 2n+1
2n is even, so 2n+1 must be odd
Question 17 [4 marks]
There are 8 counters in a bag.
3 of the counters are red.
5 of the counters are blue.
Rilee takes at random two counters from the bag.
Using a tree diagram, work out the probability that Rilee takes one counter of each colour.
Give your answer in simplest form.
Answer type: Fraction
ANSWER: \dfrac{15}{28}

The probability that Rilee takes one counter of each colour is
\dfrac{15}{56} + \dfrac{15}{56} = \dfrac{15}{28}
Question 18 [4 marks]

ABCD is a rhombus.
The coordinates of A are (2,12)
The equation of the diagonal DB is y = \dfrac{1}{3} x + 9
Find an equation of the diagonal AC.
Answer type: Multiple choice type 1
A: y = -3x + 18
B: y = 3x + 6
C: y = -3x + 6
D: y = \dfrac{1}{3}x + \dfrac{34}{3}
ANSWER: A
WOKRING:
AC is perpendicular to DB
So the gradient of AC is - \bigg(\dfrac{1}{3} \bigg)^{-1} = -3
So the equation of AC is of the form y = -3x + c
The point A(2,12) is on the line, so substitute in these values into the equation to find c
12 = -3(2) + c
12 = -6 + c
c = 18
The equation of AC is y = -3x + 18
Question 19 [4 marks]

OABC is a parallelogram.
\overrightarrow{OA} = \textbf{a} and \overrightarrow{OC} = \textbf{c}
X is the midpoint of the line AC.
OCD is a straight line such that OC:CD=k:1
Given that \overrightarrow{XD} = 2 \textbf{c} - \dfrac{1}{2} \textbf{a}
find the value of k.
Answer type: Fraction
ANSWER: \dfrac{2}{3}
WORKING:
\overrightarrow{CX} = \dfrac{1}{2} \overrightarrow{CA} = \dfrac{1}{2}(\textbf{a} - \textbf{c})
\overrightarrow{CD} = \overrightarrow{CX} + \overrightarrow{XD} = \dfrac{1}{2}(\textbf{a} - \textbf{c}) + 2\textbf{c} - \dfrac{1}{2} \textbf{a} = \dfrac{3}{2} \textbf{c}
\dfrac{\overrightarrow{OD}}{\overrightarrow{OC}} = \dfrac{k+1}{k} = \dfrac{\frac{5}{2}\textbf{c}}{\textbf{c}}
k+1 = \dfrac{5}{2} k
1 = \dfrac{3}{2} k
k = \dfrac{2}{3}
Question 20 [5 marks]
Solve algebraically the following simultaneous equations.
x^2 + y^2 = 40
y - 2x = 2
Answer type: Multiple choice type 1
A: x = 2, y = 6 and x = - \dfrac{18}{5}, y = - \dfrac{26}{5}
B: x = 2, y = 4 and x = \dfrac{9}{5}, y = - \dfrac{12}{5}
C: x = 2, y = 6 and x = - \dfrac{18}{5}, y = \dfrac{12}{5}
D: x = 6, y = 2 and x = \dfrac{9}{5}, y = - \dfrac{26}{5}
WORKING:
Rearrange the second equation, y = 2x+2, and substitute into the first equation:
x^2 + (2x+2)^2 = 40Then expand and simplify:
x^2 + 4x^2 + 4x + 4x + 4 = 40
5x^2 + 8x + 4 = 40
5x^2+ 8x - 36 = 0
(5x+18)(x-2)=0
So, x = - \dfrac{18}{5} or x = 2
Substitute these into the second equation to find y,
y = 2(2) + 2 = 6 or y = 2(- \frac{18}{5}) + 2 = - \dfrac{26}{5}
Question 21 [4 marks]
ABCD is a quadrilateral.

AB = CD
\angle ABC = \angle BCD
Choose the correct statements regarding:
Question 21(a) [1 mark]
The angles in the quadrilateral ABCD.
Answer type: Multiple choice type 1
A: \angle BAD + \angle ABC = 180 \degree
B: \angle BAD + \angle ABC = 90 \degree
C: 2\times \angle ABC + \angle BAD + \angle ADC = 360 \degree
D: \angle BAD = \angle BCD
ANSWER: C
WORKING:
Angles in a quadrilateral add up to 360 \degree.
So \angle ABC + \angle BCD + \angle BAD + \angle ADC =360 \degree
\angle ABC = \angle BCDTherefore, 2\times \angle ABC + \angle BAD + \angle ADC = 360 \degree
Question 21(b) [3 marks]
Distances between points in the quadrilateral ABCD.
Answer type: Multiple choice type 1
A: AC = BD
B: BC = AD
C: AB + CD = AD
D: AC = AD
ANSWER: A
WORKING:
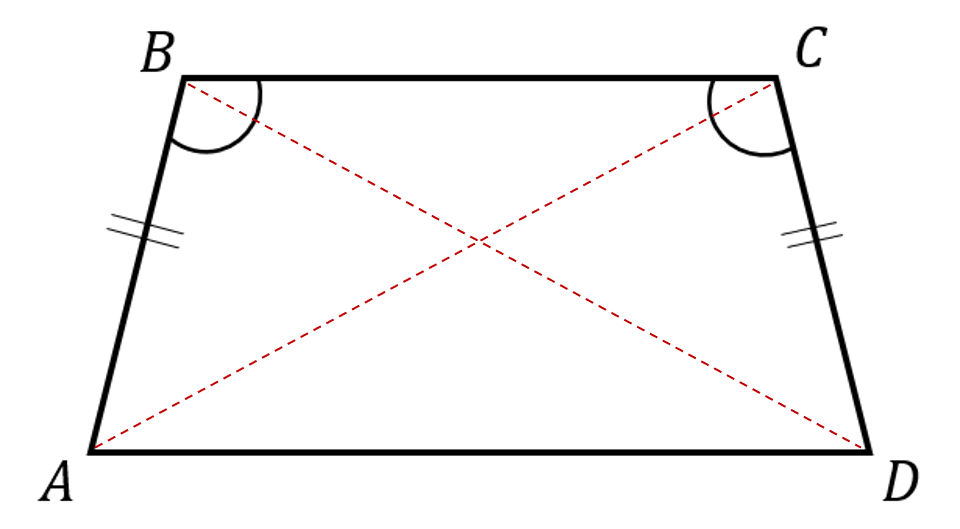
\angle ABC = \angle BCD
AB = CD
If we create two triangles using the quadrilateral, ABC and DCB, we can see that they both share a common side BC.
Then, triangle ABC \equiv triangle DCB by SAS congruency of triangles
Therefore AC = BD
Question 22
The diagram shows a shape ABCDEF.

ABEF and CBED are congruent parallelograms where AB = BC = x cm.
P is the point on AF and Q is the point on CD such that BP = BQ = 5 cm.
Given that angle ABC = 45 \degree
choose the correct equation in terms of \cos PBQ
Answer type: Multiple choice type 1
A: \cos PBQ = 1 - \dfrac{(2 - \sqrt{2})x^2}{50}
B: \cos PBQ = 1 - \dfrac{(2 - \sqrt{3})x^2}{100}
C: \cos PBQ = 1 - \dfrac{2x^2}{50}
D: \cos PBQ = 1 - \dfrac{(2 - \sqrt{2})x^2}{100}
ANSWER: A
WORKING:
\cos 45 = \dfrac{\sqrt{2}}{2}
Using the cosine rule and rearranging
PQ^2 = 5^2 + 5^2 - 2 \times 5 \times 5 \cos PBQ
PQ^2 = 50 - 50 \cos PBQ
\cos PBQ = \dfrac{50 - PQ^2}{50}
AC = PQ so AC^2 = PQ^2
Using the cosine rule
AC^2 = x^2 + x^2 - 2x^2 \cos 45
AC^2 = 2x^2 - 2x^2 \bigg(\dfrac{\sqrt{2}}{2} \bigg)
AC^2 = 2x^2 - \sqrt{2} \, x^2
AC^2 = x^2(2 - \sqrt{2})
Therefore,
\cos PBQ = \dfrac{50 - PQ^2}{50} = \dfrac{50 - x^2(2 - \sqrt{2})}{50} = 1 - \dfrac{(2 - \sqrt{2})x^2}{50}