NOTE: Q1-6 are the same as Q15-20 on June 17 Foundation Paper 3
(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1
\xi = \{ \text{even numbers less than } 20 \}
A = \{2, 6, 8, 12, 18 \}
B = \{2, 8, 16 \}
Question 1(a) [4 marks]
Choose the correct Venn diagram from the options below that represents this information.
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: A
WORKING:
Missing numbers that are not in A nor B are \{4, 10, 14 \}
Question 1(b) [2 marks]
A number is chosen at random from the universal set, \xi.
What is the probability that the number is in the set A \cap B?
Give your answer as a fraction in simplest form.
Answer type: Fraction
ANSWER: \dfrac{2}{9}
Question 2 [3 marks]
Solve the simultaneous equations
2x+3y = 8
4x-y=2
Answer type: Multiple answers type 1
ANSWER:
x = 1
y = 2
WORKING:
Multiply equation 1 by 2:
4x+6y=16
Subtract equation 2 from equation the new 1, so that the coefficients of x cancel:
(4x-4x) + (6y-(-y)) = 16-2
7y=14
y=2
Substitute y=2 into either equation, here we will put it into equation 2:
4x - 2 = 2
4x=4
x=1
Question 3
The table shows some information about the number of bedrooms 30 people have in their house.

Question 3(a) [1 mark]
Find the median number of bedrooms.
Answer type: Simple text answer
ANSWER: 3 bedrooms
WORKING:
Median is the between the 15th and 16th person, which is 3 bedrooms.
Question 3(b) [1 mark]
14 of the 30 people have 2 bathrooms in their house.
Mitch says that if you choose at random one of the 30 people, the probability that they have either 2 bathrooms or 2 bedrooms is \dfrac{22}{30} because
\dfrac{14}{30} + \dfrac{8}{30} = \dfrac{22}{30}
Is Mitch correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: B
WORKING:
No, because the number of bathrooms and number of bedrooms are not mutually exclusive – so addition is incorrect.
Question 4 [5 marks]
Nicola bakes 540 cookies.
She bakes only milk chocolate cookies, white chocolate cookies, triple chocolate cookies and raspberry cookies.
\dfrac{1}{3} of the cookies are milk chocolate.
15 \% of the cookies are white chocolate.
The ratio of the number of triple chocolate cookies to the number of raspberry cookies is 2:7
How many raspberry cookies does Nicola bake?
Answer type: Simple text answer
ANSWER: 217
WORKING:
\dfrac{1}{3} \times 540 = 180 milk chocolate cookies
0.15 \times 540 = 81 white chocolate cookies
There are 540 - 180 - 81 = 279 triple choc cookies and raspberry cookies
The ratio of triple chocolate cookies to the number of raspberry cookies is 2:7, so there are 9 parts
One part is worth 279 \div 9 = 31 cookies
The ratio of triple chocolate cookies to the number of raspberry cookies is therefore 62:217, by multiplying the ratio by 1 part (31)
Hence, Nicola bakes 217 raspberry cookies
Question 5 [4 marks]
In the diagram, AB, BC and CD are sides of a regular polygon P.

How many sides does polygon P have?
Answer type: Simple text answer
ANSWER: 15
WORKING:
The polygon shown in full is a decagon (10 sides)
\angle B = \dfrac{180}{10} (10-2) = 144 \degree
An equilateral triangle has all angles of 60 \degree
The interior angle of polygon P = 360 - 144 - 60 = 156 \degree
The exterior angle of polygon P = 180 - 156 = 24 \degree
The number of sides of polygon P = \dfrac{360}{24} = 15
Question 6 [4 marks]
The density of gin is 0.94 g/cm^3
The density of sugar syrup is 1.3 g/cm^3
The density of lime juice is 1.15 g/cm^3
60 cm^3 of gin is mixed with 20 cm^3 of sugar syrup and 30 cm^3 of lime juice to make a Southside cocktail drink, with a volume of 110 cm^3.
Work out the density of the drink.
Give your answer to 2 decimal places.
Answer type: Simple text answer
ANSWER: 1.06 g/cm^3
WORKING:
\text{density} = \text{mass} \div \text{volume}
Gin mass = 0.94 \times 60 = 56.4 g
Syrup mass = 1.3 \times 20 = 26 g
Lime juice mass = 1.15 \times 30 = 34.5 g
Total mass = 56.4 + 26 + 34.5 = 116.9 g
Total density = \dfrac{116.9}{110} = 106 g/cm^3 (2 dp)
Question 7 [2 marks]
ABC is a right-angled triangle.

Calculate the length of BC.
Give your answer to 3 significant figures.
Answer type: Simple text answer
ANSWER: 14.9 cm
WORKING:
\cos(34) = \dfrac{BC}{18}
BC = 18 \cos(34) = 14.9 cm
Question 8 [4 marks]
A square, with sides of length x cm, is inside a circle.
Each vertex of the square lies on the circumference of the circle.
The area of the circle is 64 cm^2
Work out the value of x.
Give your answer correct to 2 decimal places.
Answer type: Simple text answer
ANSWER: 6.38 cm
WORKING:
\pi r^2 = 64
r^2 = \dfrac{64}{\pi}
Using Pythagoras, for a right angled triangle with hypotenuse x, as one side of the square and the other two sides the radius, gives
r^2 + r^2 = x^2
2r^2 = x^2
Substitute r^2 from above into this equation, giving
x^2 = 2 \times \dfrac{64}{\pi}
x = \sqrt{2 \times \dfrac{64}{\pi}} = 6.38 cm (2 dp)
(x must be positive, since length is a physical quantity)
Question 9
The box plot below shows information about the distribution of the ages males in a restaurant.
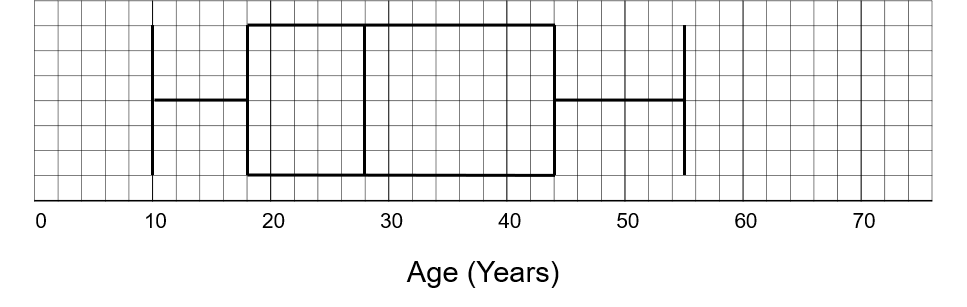
Question 9(a) [2 marks]
Work out the interquartile range for the age of these males.
Answer type: Simple text answer
ANSWER: 26
WORKING:
44 - 18 = 26
Question 9(b) [2 marks]
The table below shows information about the distribution of the ages females in a restaurant.

Choose the correct box plot drawn from the information provided in the table above.
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: A
Question 9(c) [1 mark]
Craig says,
“The box plots show that the females in the restaurant are older than the males.”
Is Craig correct?
Answer type: Multiple choice type 1
A: Yes
B: No
ANSWER: A
WORKING:
The median for the females is greater than that for males.
Question 10 [3 marks]
Nigel invests £4000 into a bank account for 4 years.
The investment gets compound interest of x\% per annum.
At the end of 4 years the investment is worth £4862.03
Work out the value of x, to the nearest whole number.
Answer type: Simple text answer
ANSWER: 5 \%
WORKING:
4000 \times (1+\dfrac{x}{100})^4 = 4862.03
(1+\dfrac{x}{100})^4 = \dfrac{4862.03}{4000}
1+\dfrac{x}{100} = \sqrt[4]{\dfrac{4862.03}{4000}} = 1.05
x = 5 \%
Question 11 [2 marks]
Ella is choosing a top and a skirt to buy for Saturday night.
At the clothes shop there are 12 different types of top and some different types of skirt.
There are 192 different ways of choosing one top and one skirt.
How many different types of skirts are there?
Answer type: Simple text answer
ANSWER: 16
WORKING:
Number of different skirts = 192 \div 12 = 16
Question 12
The points A, B, C and D lie in order on a straight line.
AB:BD = 2:3
AC:CD = 9:11
What is AB:BC:CD?
Answer type: Multiple choice type 1
A: 8:1:11
B: 6:3:11
C: 2:6:11
D: 8:3:11
ANSWER: A
WORKING:
AB:BD consists of 5 parts.
AC:CD consists of 20 parts.
Multiply the ratio AB:BD by 4 so that it also has 20 parts, giving 8:12
AB:BC:CD = 8: 9-8:11 = 8:1:11
Question 13 [4 marks]
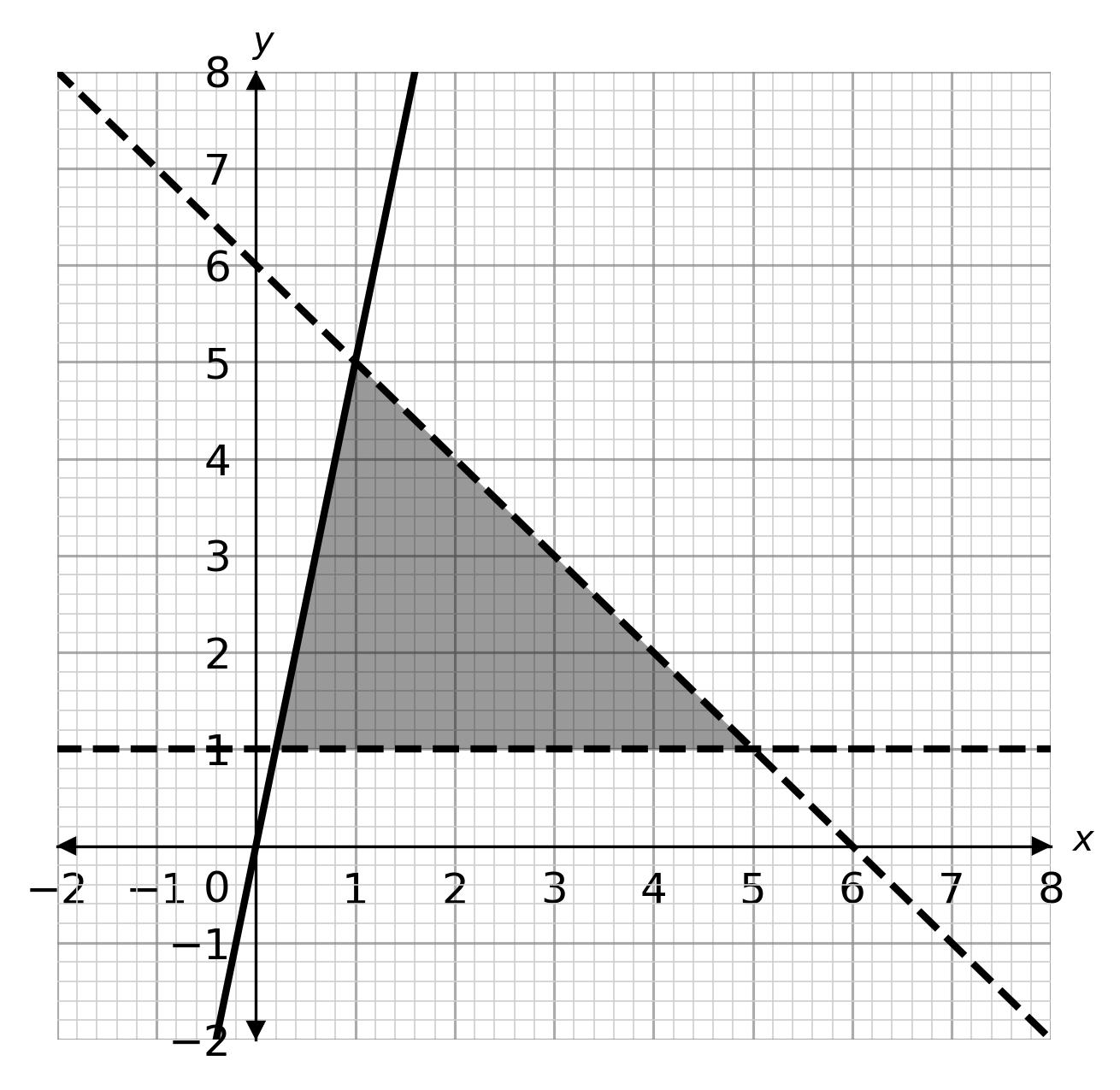
What three inequalities define the shaded region?
Answer type: Multiple choice type 1
A: y > 1, y \leq 5x, y < -x + 6
B: y \geq 1, y < 5x, y \leq -x + 6
C: y < 1, y \geq 5x, y > -x + 6
D: y \leq 1, y > 5x, y \geq -x + 6
ANSWER: A
WORKING:
A solid line means \leq or \geq and a dashed line means < or >
The shaded area lies above the line y=1, and the line is dashed, so we have y > 1
The shaded area lies below the line y=5x, and the line is solid, so we have y \leq 5x
The shaded area lies below the line y=-x+6, and the line is dashed, so we have y < -x+6
Question 14
Answer the following questions.
Question 14(a) [3 marks]
Choose the correct simplification for the following expression
\dfrac{x^2 - 9}{2x^2 + 9x + 9}
Answer type: Multiple choice type 1
A: \dfrac{x-3}{2x+3}
B: \dfrac{2x+3}{x-3}
C: \dfrac{x+3}{2x+3}
D: \dfrac{x+3}{2x-3}
ANSWER: A
WORKING:
\dfrac{x^2 - 9}{2x^2 + 9x + 9}
= \dfrac{(x-3)(x+3)}{(2x+3)(x+3)}
= \dfrac{x-3}{2x+3}
Question 14(b) [3 marks]
Make y the subject of the formula z = \dfrac{12(x-5y)}{7y}
Choose the correct expression.
Answer type: Multiple choice type 1
A: y = \dfrac{12x}{7z+60}
B: y = \dfrac{12x-60}{7z}
C: y = \dfrac{12x}{7z+5}
D: y = \dfrac{12z}{7x+12}
ANSWER: A
WORKING:
z = \dfrac{12(x-5y)}{7y}
7yz = 12x-60y
7yz + 60y = 12x
y(7z+60) = 12x
y = \dfrac{12x}{7z+60}
Question 15 [5 marks]

The area of the triangle ABC is 8 cm^2.
Calculate the value of x, giving your answer to 3 significant figures.
Answer type: Simple text answer
ANSWER: 4.32 cm
WORKING:
Area =\dfrac{1}{2} ab \sin C = 8
\dfrac{1}{2} (x-1)(2x+1) \sin 30 = 8
\dfrac{1}{2}(2x^2-x-1) \times \dfrac{1}{2} = 8
\dfrac{1}{4}(2x^2-x-1) = 8
2x^2-x-1 = 32
2x^2-x-33=0
x must be a positive value, since length is a physical quantity, so
x = \dfrac{1+\sqrt{(-1)^2-4 \times 2 \times -33}}{2 \times 2} = 4.32 (3 sf)
Question 16
Using x_{n+1} = - 3 - \dfrac{3}{x_n^2}
with x_0 = -3.5
Question 16(a) [3 marks]
Find the values of x_1, x_2 and x_3
Give all answers to 3 decimal places.
Answer type: Multiple answers type 1
ANSWER:
x_1 = -3.245
x_2 = -3.285
x_3 = -3.278
WORKING:
x_1 = - 3 - \dfrac{3}{(-3.5)^2} = -3.245...x_2 = - 3 - \dfrac{3}{(-3.245...)^2} = -3.285...
x_3 = - 3 - \dfrac{3}{(-3.285...)^2} = -3.278...
Question 16(b)
What is the relationship between the values of x_1, x_2 and x_3 and the equation x^3 + 3x^2 + 3 = 0?
Answer type: Multiple choice type 2
A: The equation can be rearranged into the iterative form, and the iterations x_1, x_2 and x_3 estimate the solutions to the equation.
B: They are brothers and sisters.
C: There is no relationship.
D: x_1, x_2 and x_3 added together equals 0
ANSWER: A
Question 17
A train travelled along a track in 80 minutes, correct to the nearest 5 minutes.
Mahmood finds out that the track is 200 km long, measured to the nearest 10 km.
Question 17(a) [4 marks]
What is the maximum average speed of the train?
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 158.7 km/h
WORKING:
195 < \text{d} < 205
77.5 < \text{t} < 82.5
Max Speed = \dfrac{\text{d}}{\text{t}} = \dfrac{205}{77.5} \times 60 = 158.7 km/h
(We multiplied by 60 to convert from minutes to hours)
Question 17(b) [1 mark]
If the track was measured correct to 5 km instead, how would this affect your answer to part (a)?
Answer type: Multiple choice type 1
A: The answer would increase.
B: The answer would decrease.
ANSWER: B
WORKING:
The error interval for the distance would decrease, so the numerator of the fraction would decrease, so the maximum average speed would decrease.
(There would less distance travelled in the same time, so the maximum speed would drop.)
Question 18 [5 marks]
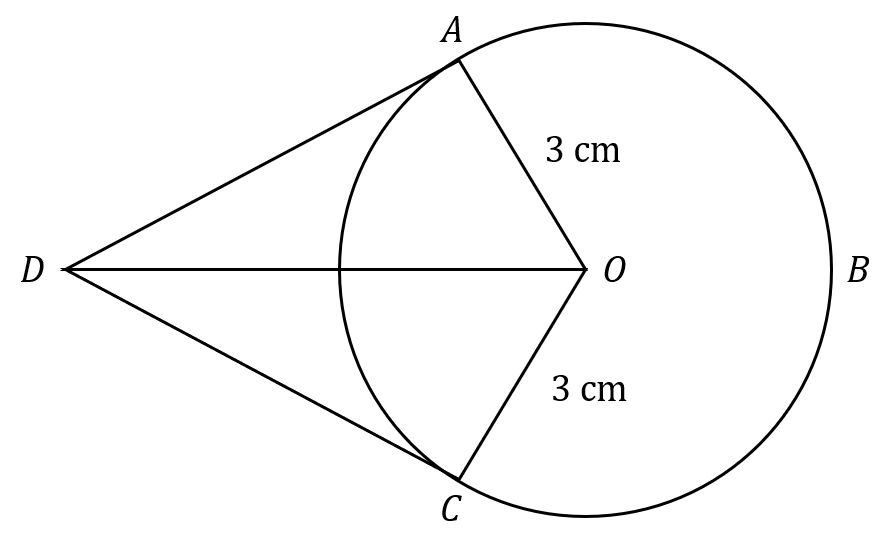
A, B and C are points on a circle of radius 3 cm, with centre O.
AD and CD are tangents to the circle.
OD = 5 cm
What it the length of the arc ABC?
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 13.3 cm
WORKING:
\angle OAD and \angle OCD are 90 \degree, since a tangent to a circle forms a right angle with the radius.
Using SOHCAHTOA,
\cos DOA = \dfrac{3}{5} DOA = \cos^{-1}\bigg(\dfrac{3}{5} \bigg) \approx 53.130 \degree\angle DOC = \angle DOA = 53.130 \degree
So, \angle AOC = 53.130 + 53.130 = 106.260 \degree
Reflex angle O = 360 - 106.260 = 253.740 \degree
Length of arc ABC = \dfrac{253.740}{360} \times 2 \times \pi \times 3 = 13.3 cm (1 dp)
Question 19 [3 marks]
Solve 3x^2 - x - 2 < 0
Choose the correct answer.
Answer type: Multiple choice type 1
A: -\frac{2}{3} < x < 1
B: x < - \frac{2}{3} and x > 1
C: -1 < x <\frac{2}{3}
D: x < - 1 and x > \frac{2}{3}
ANSWER: A
WORKING:
Let
3x^2 - x - 2 = 0
(3x+2)(x-1) = 0
x = -\frac{2}{3} and x = 1
We want (3x+2)(x-1) < 0, giving solutions of -\frac{2}{3} < x < 1
Question 20
The equation of a circle C is x^2 + y^2 = 25
The circle C is translated by the vector \begin{pmatrix}2\\0\end{pmatrix} to give a new circle, D
Question 20(a) [1 mark]
What is the radius of circle D?
Answer type: Simple text answer
ANSWER: 5
WORKING:
\sqrt{25} = 5
Question 20(b) [1 mark]
What is the centre of circle D?
Answer type: Multiple choice type 1
A: (2,0)
B: (0,0)
C: (0,2)
D: (-2,0)
ANSWER: A
WORKING:
The centre of circle C is (0,0), and this is translated by \begin{pmatrix}2\\0\end{pmatrix}, so the centre of circle D is (2,0)
Question 20(c) [2 marks]
What are the points of intersection with the x-axis of circle D?
Answer type: Multiple choice type 1
A: (-3,0) and (7,0)
B: (0,5) and (0,-5)
C: (0,-3) and (0,7)
D: (-7,0) and (0,3)
ANSWER: A
WORKING:
The points of intersection with the x-axis of circle C are (5,0) and (-5,0)
Circle C is translated by \begin{pmatrix}2\\0\end{pmatrix} to give circle D, so the points of intersection with the x-axis of circle D are found by adding 2 to the x coordinates of the the points of intersection with the x-axis of circle C.
We get (-5+2,0) = (-3,0) and (5+2,0) = (7,0)
