NOTE: Q17-23 are the same as Q1-7 on June 17 Higher Paper 2
(DOESNT NEED CHECKING TWICE – CHANGE BOTH PAPERS IF THERE IS AN ERROR ON BOTH)
Question 1
Question 1(a) [1 mark]
Simplify 6t - 2t + t
Answer type: Multiple choice type 1
A: 5t
B: 3t
C: 4t
D: 6t
ANSWER: A
WORKING:
6t - 2t + t = 5t
Question 1(b) [1 mark]
Simplify x^2 + x^2
Answer type: Multiple choice type 1
A: 2x^2
B: x^2
C: 2x
D: 4x
ANSWER: A
WORKING:
x^2 + x^2 = 2x^2
Question 1(c) [2 marks]
Simplify 6 + 10a + 3b - 6a + 2b
Answer type: Multiple choice type 1
A: 6 + 4a + 5b
B: 4a + 5b
C: 6 + 5a + 4b
D: 6 + 16a + 5b
ANSWER: A
WORKING:
6 + 10a + 3b - 6a + 2b = 6 + 4a + 5b
Question 2 [1 mark]
Write 147.51 correct to 2 significant figures.
Answer type: Simple text answer
ANSWER: 150
Question 3
A teacher asks the students in Year 5 what their favourite type of fruit is.
The dual bar chart below shows some of the results.

Question 3(a) [1 mark]
What is the most popular type of fruit chosen by the boys?
Answer type: Multiple choice type 1
A: Orange
B: Banana
C: Apple
D: Grapes
E: Other
ANSWER: B
WORKING:
The tallest bar for boys is banana, which has a frequency of 14
Question 3(b) [1 mark]
How many girls chose apple as their favourite fruit?
Answer type: Simple text answer
ANSWER: 7
Question 3(c) [1 mark]
How many more students chose orange as their favourite fruit than grapes?
Answer type: Simple Text
ANSWER: 6
WORKING:
Number of students that chose orange = 12 + 9 = 21
Number of students that chose grapes = 4 + 11 = 15
Difference = 21 - 15 = 6
Question 3(d) [2 marks]
The number of students in year 4 is the same as the number of students in year 5.
What is the total number of students in years 4 and 5?
Answer type: Simple text answer
ANSWER: 160
Year 5 total frequency = 12+9+14+10+6+7+4+11+2+5 = 80
So there are 80 students in year 4 also.
Total number of students in year 4 and 5 = 80 + 80 = 160
Question 4 [2 marks]
Here are 4 fractions
\dfrac{3}{4} , \,\, \dfrac{17}{20}, \,\, \dfrac{4}{5}, \,\, \dfrac{7}{10}
Write these fractions in order of size, starting with the smallest.
Answer type: Multiple choice type 1
A: \dfrac{7}{10} , \,\, \dfrac{3}{4}, \,\, \dfrac{4}{5}, \,\, \dfrac{17}{20}
B: \dfrac{17}{20} , \,\, \dfrac{4}{5}, \,\, \dfrac{3}{4}, \,\, \dfrac{7}{10}
C: \dfrac{3}{4} , \,\, \dfrac{7}{10}, \,\, \dfrac{4}{5}, \,\, \dfrac{17}{20}
D: \dfrac{7}{10} , \,\, \dfrac{3}{4}, \,\, \dfrac{17}{20}, \,\, \dfrac{4}{5}
ANSWER: A
WORKING:
Write the fractions with the same common denominator, 20
\dfrac{15}{20} , \,\, \dfrac{17}{20}, \,\, \dfrac{16}{20}, \,\, \dfrac{14}{20}
Then put in order, starting with the smallest.
\dfrac{14}{20} , \,\, \dfrac{15}{20}, \,\, \dfrac{16}{20}, \,\, \dfrac{17}{20}
Then, write the fractions in original form, in order
\dfrac{7}{10} , \,\, \dfrac{3}{4}, \,\, \dfrac{4}{5}, \,\, \dfrac{17}{20}
Question 5
Question 5(a) [1 mark]
Jacob sells books in a bookshop.
The tally chart shows information about the number of books Jacob sold on Friday, Saturday and Sunday.

What is wrong with the tally chart?
Answer type: Multiple choice type 1
A: The frequency and tally are different for Friday
B: The frequency and tally are different for Saturday
C: The frequency and tally are different for Sunday
D: The headings are incorrect
ANSWER: B
WORKING:
The tally for Saturday is 12, but the frequency says 11, which is wrong.
Question 5(b) [1 mark]
Jacob drew the pictogram below to show the information for Saturday and Sunday.

What is wrong with this pictogram?
Answer type: Multiple choice type 1
A: The pictogram is wrong for Saturday
B: The pictogram is wrong for Sunday
ANSWER: B
Question 6 [4 marks]
There are 85 notes in a jar.
\dfrac{1}{5} of the notes are £20 notes
29 of the notes are £10 notes
The rest of the notes are £5 notes
Calculate the total value of the money in the jar.
Answer type: Simple text answer
ANSWER: £825
WORKING:
Number of £20 notes = \dfrac{1}{5} \times 85 = 17
17 \times £20 = £340
Number of £10 notes = 29
29 \times £10 = £290
Number of £5 notes = 85-17-29 = 39
39 \times £5 = £195
Total = £340 + £290 + £195 = £825
Question 7 [1 mark]
The probability that a vaccine will cause long term health issues is 0.025
What is the probability that the vaccine will not cause long term health issues?
Answer type: Simple text answer
ANSWER: 0.975
WORKING:
1 - 0.025 = 0.975
Question 8
Here is a list of numbers
31 \,\,\,\, 32 \,\,\,\, 33 \,\,\,\, 34 \,\,\,\, 35 \,\,\,\, 36 \,\,\,\, 37 \,\,\,\, 38 \,\,\,\, 39
Question 8(a) [1 mark]
From the numbers in the list, write down a square number.
Answer type: Simple text answer
ANSWER: 36
Question 8(b) [1 mark]
From the numbers in the list, write down a number that is both a multiple of 5 and 7
Answer type: Simple text answer
ANSWER: 35
Question 8(c) [1 mark]
What are the prime numbers from the list?
Answer type: Multiple choice type 1
A: 31, 37
B: 31
C: 31, 33, 35, 37, 39
D: 31, 33, 37
ANSWER: A
Question 9 [3 marks]

Find the value of x
Answer type: Simple text answer
ANSWER: 30 \degree
WORKING:
90 + 4x + 5x = 360
90 + 9x = 360
9x = 270
x = 30 \degree
Question 10 [4 marks]
Shirley needs to buy 300 pens.
Below is some information about the cost of pens in two different shops.

Shirley wants to buy the pens as cheaply as possible.
Which shop should Shirley buy the 300 pens from?
Answer type: Multiple choice type 1
A: World of Pens
B: Stationary 4 U
ANSWER: B
WORKING:
World of Pens:
5 \times 2 + 5 = 15\dfrac{300}{15} = 20 sets of the offer
Cost = 20 \times 2 \times £0.99 = £39.60
Stationary 4 U:
\dfrac{300}{25} = 12 packs
Cost = 12 \times £3.25 = £39.00
Stationary 4 U is better value.
Question 11
You can use the following graph to change between kilograms and pounds.

Question 11(a) [1 mark]
Change 3 kg into pounds.
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 6.6 lbs
Question 11(b) [3 marks]
Haroon weighs 13 stone 3 pounds.
1 stone = 14 pounds
To the nearest whole number, what is Haroon’s weight in kilograms?
Answer type: Multiple choice type 1
A: 84 kg
B: 96 kg
C: 72 kg
D: 88 kg
ANSWER: A
WORKING:
13 stone 3 pounds = 13 \times 14 + 3 = 185 pounds
From the graph, 1 kg = 2.2 lbs
Weight in kg = 185 \div 2.2 = 84 kg (nearest whole number)
Question 12 [2 marks]
Calculate \dfrac{\sqrt{23.6 - 7.9}}{(3.5 - 0.08)^2}
Give your answer to 5 decimal places.
Answer type: Simple text answer
ANSWER: 0.33876
WORKING:
\dfrac{\sqrt{23.6 - 7.9}}{(3.5 - 0.08)^2} = \dfrac{3.962322...}{11.6964} = 0.338764... = 0.33876 (5 dp)
Question 13

Question 13(a) [2 marks]
Choose the correct rotation of shape A 90 \degree anticlockwise about the centre O.
Answer type: Multiple choice type 1
A:

B:

C:
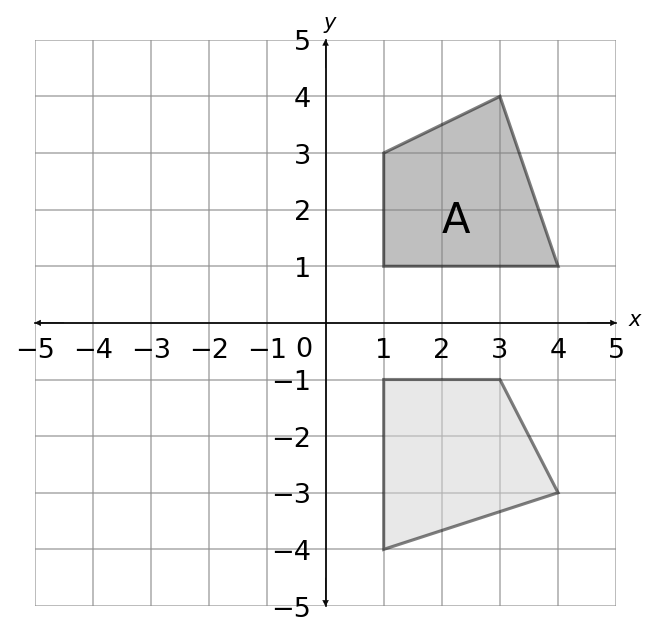
D:

ANSWER: A
Question 13(b) [2 marks]

What is the single transformation that maps triangle A onto triangle B?
Answer type: Multiple choice type 1
A: Reflection in the y axis
B: Reflection in the x axis
C: Reflection in the line y=x
D: Rotation 90 \degree anticlockwise about the centre O
ANSWER: A
Question 14
Question 14(a) [1 mark]
Factorise 8 - 4b
Answer type: Multiple choice type 1
A: 4(2-b)
B: 2(4-b)
C: 4(b-2)
D: 2(b-4)
ANSWER: A
Question 14(b) [2 marks]
Factorise fully 3x^2y + 9xy
Answer type: Multiple choice type 1
A: 3xy(x+3)
B: 3x(y+3x)
C: 3y(x+3)
D: 3(x+3y)
ANSWER: A
WORKING:
3x^2y + 9xy = 3(x^2y + 3xy) = 3x(xy + 3y) = 3xy(x+3)
Question 15
Question 15(a) [1 mark]
Write 9.2 \times 10^{-2} as an ordinary number.
Answer type: Simple text answer
ANSWER: 0.092
Question 15(b) [2 marks]
Calculate (3.5 \times 10^2) \times (7.2 \times 10^5)
Give your answer in standard form.
Answer type: Multiple choice type 1
A: 2.52 \times 10^8
B: 25.2 \times 10^7
C: 2.52 \times 10^6
D: 2.52 \times 10^7
ANSWER: A
WORKING:
(3.5 \times 10^2) \times (7.2 \times 10^5)
= 25.2 \times 10^{2+5}
= 25.2 \times 10^7
= 2.52 \times 10^8
Question 16 [3 marks]
A and B are two points on a map.

The distance between A and B is 50 m
Point C is 40 metres from point B
Point C is equidistant from point A and point B.
How many possible points are there for point C?
Answer type: Simple text answer
ANSWER: 2
WORKING:
The diagram does not need to be accurate for this question.
Draw a perpendicular bisector through points A and B
Draw a locus of points around point B

There are two possible points for C, as seen in the diagram above.
Question 17 [3 marks]
The table shows the probabilities that a biased dice will land 1, 2, 3, 4 and 5

Ron rolls the biased dice 500 times.
Work out an estimate for the total number of times the dice will land on 5 or on 6
Answer type: Simple text answer
ANSWER: 235
WORKING:
\text{P(Landing on a 6)} = 1 - 0.05 - 0.23 - 0.09 - 0.16 - 0.28 = 0.19
\text{P(Landing on a 5 or a 6)} = 0.28 + 0.19 = 0.47
The biased dice will land on a 5 or on a 6 approximately
500 \times 0.47 = 235 times
Question 18 [5 marks]
On Sunday, some adults and some children were in a stadium
The ratio of the number of adults to the number of children was 3:2
Each person had a seat in the North stand or the East stand.
\dfrac{4}{5} of the children had seats in the East stand.
120 children had seats in the North stand.
There are exactly 2000 seats in the stadium.
On this Sunday, what percentage of the stadium seats were filled?
Answer type: Simple text answer
ANSWER: 75 \%
WORKING:
1 - \dfrac{4}{5} = \dfrac{1}{5} of the children had seats in the North stand, which was 120 children.
Therefore there were 120 \times 5 = 600 children in the stadium.
The ratio of adults to children is 3:2, so the ratio scaled up is 900:600
So, there are 900 + 600 = 1500 people in the stadium.
The \% of the stadium that is full is \dfrac{1500}{2000} \times 100 = 75 \%
Question 19 [4 marks]
The diagram shows a 3D shape.

Choose the correct diagram below that shows the front and side elevation of the 3D shape above, drawn on a centimetre grid.
Answer type: Multiple choice type 1
A:

B:

C:

D:

ANSWER: A
Question 20
Oscar drove 100 km from Hull to Leeds.
He then drove 72 km from Leeds to Manchester.
Oscar’s average speed from Hull to Leeds was 80 km/h.
Oscar took 63 minutes to drive from Leeds to Manchester.
Question 20(a) [4 marks]
Work out Oscar’s average speed for his total drive from Hull to Manchester.
Give your answer to 1 decimal place.
Answer type: Simple text answer
ANSWER: 74.8 km/h
WORKING:
Time from Hull to Leeds: \dfrac{100}{80} = 1.25 hours =75 minutes
Total distance = 100 + 72 = 172 km
Total time = 75 + 63 = 138 minutes = 2.3 hours
Average speed = \dfrac{172}{2.3} = 74.8 km/h (1 dp)
Question 20(b) [1 mark]
Francis drove straight from Hull to Manchester.
The distance from Hull to Manchester is 160 km.
She took 2 hours.
Who had the fastest average speed?
Answer type: Multiple choice type 1
A: Oscar
B: Francis
ANSWER: B
WORKING:
The average speed for Francis is \dfrac{160}{2} = 80 km/h.
Therefore Francis had the fastest average speed.
Question 21

ABC and EDC are straight lines.
DB is parallel to EA.
EC = 7 m
DC = 2.8 m
DB = 2.2 m
Question 21(a) [2 marks]
What is the length of AE?
Answer type: Simple text answer
ANSWER: 5.5 m
WORKING:
Scale factor = \dfrac{EC}{DC} = \dfrac{7}{2.8} = 2.5
AE = 2.2 \times 2.5 = 5.5 m
Question 21(b) [2 marks]
AC = 6 m
What is the length of AB?
Answer type: Simple text answer
ANSWER: 3.6 m
WORKING:
BC = 6 \div 2.5 = 2.4 m
AB = AC - BC = 6 - 2.4 = 3.6 m
Question 22 [3 marks]
Junet wants to invest £20000 for 4 years in a bank.

Which bank should Junet choose, to maximise his investment?
Answer type: Multiple choice type 1
A: Bank A
B: Bank B
ANSWER: B
WORKING:
A: £20000 \times 1.015^4 = £21227.27
B: £20000 \times 1.04 \times 1.01^3 = £21430.26
Junet should choose bank B.
Question 23 [2 marks]
A number, x, is rounded to 2 decimal places.
The result is 8.64
What is the error interval for x?
Answer type: Multiple choice type 1
A: 8.635 \leq x < 8.645
B: 8.63 \leq x < 8.65
C: 8.6 \leq x < 8.7
D: 8.6355 \leq x < 8.6455
ANSWER: A
Question 24 [3 marks]
Solve x^2 + 7x - 44 = 0
Answer type: Multiple answers type 2 (Can be either way round)
ANSWER:
x = -11
x = 4
WORKING:
Factorise the equation and solve for x:
x^2 + 7x - 44 = 0
(x+11)(x-4) = 0
x +11 = 0, so x = 11
x-4 = 0, so x = 4
Question 25
Here are the first five terms of an arithmetic sequence
3 \,\,\, 7 \,\,\, 11 \,\,\, 15 \,\,\, 19
Question 25(a) [2 marks]
Find an expression, in terms of n, for the nth term of this sequence.
Answer type: Multiple choice type 1
A: 4n-1
B: 4n+1
C: 4-n
D: n+4
ANSWER: A
WORKING:
The difference between each term is 4
Original sequence: 3 \,\,\, 7 \,\,\, 11 \,\,\, 15 \,\,\, 19
4n: 4 \,\,\, 8 \,\,\, 12 \,\,\, 16 \,\,\, 20
Difference: -1 \,\,\, -1 \,\,\, -1 \,\,\, -1 \,\,\, -1
The nth term is 4n - 1
Question 25(b) [1 mark]
The nth term of a different sequence is 4n^2
What is the 3rd term of the sequence?
Answer type: Simple text answer
ANSWER: 36
WORKING:
4 \times (3)^2 = 36